Státnice I3: Stochastické metody a jejich aplikace v počítačové lingvistice

Z ωικι.matfyz.cz
Přejít na: navigace, hledání

Zpracováno na základě poznámek z Pravděpodobnostních metod, Statistických metod zpracování přirozených jazyků I a Úvodu do strojového učení. -- Tuetschek 15:23, 24 Aug 2010 (CEST)

Literatura:

  • Manning, Schütze -- Foundations of Statistical NLP
  • Mitchell -- Machine Learning

Teorie informace

Pravděpodobnost

Jev, pravděpodobnost

Jev $ A\,\! $ je podmnožina libovolných výstupů (např. nějakého experimentu) -- sample space $ \Omega\,\! $. Prostor jevů $ 2^{\Omega}\,\! $ je množina všech možných jevů.

Pravděpodobnost je zobrazení $ p:2^{\Omega}\to[0,1]\,\! $, pro kterou platí:

  • $ p(\Omega) = 1\,\! $,
  • pro $ A_i, i\in I\,\! $ takové, že $ A_{i_j} \cap A_{i_k} = \emptyset\,\; $ platí $ p(\cup A_i)=\sum_i p(A_i)\,\! $

Důsledky -- $ p(\emptyset) = 0\,\! $, $ p(\bar{A})=1-p(A)\,\! $, $ A\subseteq B\Rightarrow p(A)\leq p(B)\,\! $, $ \sum_{a\in\Omega} p(a)=1\,\! $.

Spojená a podmíněná pravděpodobnost

Spojená (joint) pravděpodobnost dvou jevů $ A,B\,\; $ je $ p(A,B) = p(A \cap B)\,\; $. Podmíněná pravděpodobnost (pravděpodobnost $ A\,\! $, jestliže $ B\,\! $ už nastalo) je:

$ p(A|B) = \frac{p(A,B)}{p(B)}\,\! $

Přímým důsledkem je řetězové pravdilo: $ p(A_1,A_2,\dots,A_n) = p(A_1|A_2,\dots,A_n)\cdot p(A_2|A_3,\dots,A_n)\cdot \dots \cdot p(A_n)\,\! $

Bayesova věta

Bayesova věta vychází z toho, že $ p(A|B)\cdot p(B) = p(B|A)\cdot p(A)\,\! $ což plyne z $ p(A,B)=p(B,A)\,\! $. Proto platí:

$ p(A|B) = p(B|A)\cdot\frac{p(A)}{p(B)}\,\! $

Pokud $ p(A|B) = p(B)\,\! $ jsou $ A\,\! $ a $ B\,\! $ nezávislé jevy.

Zlaté pravidlo statistického zpracování jazyka se hodí pro zjištění, který jev $ A\,\! $ je nejpravděpodobnější za předpokladu, že nastalo $ B\,\! $ a nelze dobře odhadnout $ p(A|B)\,\! $. Přes všechny jevy $ A\,\! $:

$ \arg\max_A p(A|B) = \arg\max_A p(B|A)\cdot\frac{p(A)}{p(B)} = \arg\max_A p(B|A)p(A)\,\! $

Náhodné veličiny, rozdělení

Náhodná veličina je funkce $ X:\Omega\to Q\,\! $ (často $ Q\equiv \mathbb{R}\,\! $, nebo jde o spočetnou množinu pro diskrétní náhodné veličiny). Střední (očekáváná) hodnota je průměr náhodné veličiny -- v diskrétním případě vychází $ E(X) = \sum_{x\in X(\Omega)} x\cdot p_X(x)\,\! $.


Rozdělení (distribuce) pravděpodobnosti potom je funkce $ p_X(x) = p(X=x) \,^{\mathrm{def}}\!\!\!\!\!\!\! = p(A_X)\,\! $, kde $ A_X = \{a\in\Omega | X(a) = x\}\,\! $.

Spojené rozdělení je $ p_{X,Y}(x,y)\,\! $ a podmíněné rozdělení je $ p_{X|Y}(x|y)\,\! $. Bayesova věta a řetězové pravidlo platí i pro rozdělení.

Častá rozdělení pravděpodobnosti:

  • u diskrétních náhodných veličin je nejčastější binomické -- $ p(r|n) = \mathbf{}\binom{n}{r} / 2^n\,\! $
  • u spojitých veličin normální (Gaussovo) -- $ p(x|\mu,\sigma) = (\sigma\sqrt{2\pi})^{-1}\cdot \exp(-\frac{(x-\mu)^2}{2\sigma^2})\,\! $.

Entropie

Entropie je míra nejistoty. Označuje nejmenší průměrný počet bitů potřebný k zakódování "zprávy" -- výstupu nějaké náhodné veličiny. Mějme $ p_X(x)\,\! $ distribuci náhodné veličiny $ X\,\! $, jejíž hodnoty jsou v množině1 $ \Omega\,\! $. Potom se entropie spočítá následovně:

$ H(X) = - \sum_{x\in\Omega} p(x) \log_2 p(x)\,\! $

Jednotky entropie jsou bity (používáme-li dvojkový logaritmus). Alternativní notace: $ H(X) = H_p(X) = H(p) = H_X(p) = H(p_X)\,\! $. Platí, že $ H(p) = 0\,\! $ pokud známe výsledek předem, tj. $ \exists x\in\Omega: p(x) = 1 \wedge \forall y\in\Omega, y\neq x: p(y) = 0\,\! $. Horní hranice hodnot není, ale $ |\Omega| = n: H(p) \leq \log_2 n\,\! $.

Alternativní definice: protože $ E(X) = \sum_{x\in \Omega} p_X(x)\cdot x\,\! $, platí pro náhodnou veličinu $ X\to\Omega\,\! $, že $ H(p_X) = - \sum_{x\in \Omega} p_X(x) \log_2 p_X(x) = \sum_{x\in \Omega} p_X(x) \log_2 (\frac{1}{p_X(x)})\,\! $ $ = E(\log_2(\frac{1}{p_X(x)})).\,\! $

Perplexity je jiné vyjádření míry nejistoty -- $ G(p) = 2^{H(p)}\,\! $.

Spojená a podmíněná entropie

Spojená entropie dvou náhodných veličin $ X\to\Omega\,\! $, $ Y\to\Psi\,\! $ se počítá tak, že považujeme $ (X,Y)\,\! $ za jeden jev. Potom $ H(X,Y) = -\sum_{x\in\Omega}\sum_{y\in\Psi} p(x,y)\log_2 p(x,y)\,\! $.

Podmíněná entropie se definuje jako $ H(Y|X) \,^{\mathrm{def}}\!\!\!\!\!\!\! = \sum_{x\in\Omega} p(x)\cdot H(Y|X = x)\,\! $. Protože $ p(x)\cdot p(y|x) = p(x,y)\,\! $, dá se to ekvivalentně zapsat následujícím způsobem:

$ -\sum_{x\in\Omega} p(x) \sum_{y\in\Psi} p(y|x)\log_2 p(y|x) = -\sum_{x\in\Omega,y\in\Psi} p(x,y)\log_2 p(y|x)\,\!\,\! $

Vlastnosti entropie

  • Je nezáporná ($ p(x)\geq 0\,\! $, $ \log_2 p(x)\leq 0\,\! $).
  • Řetězové pravidlo: $ H(X,Y) = H(Y|X) + H(X)\,\! $ (z definice a vlastností logaritmu)
  • Podmíněná entropie je menší nebo rovna než nepodmíněná. Z toho $ H(X,Y)\leq H(X) + H(Y)\,\! $, rovnost pro nezávislé jevy.
  • $ H(p)\,\! $ je konkávní funkce ($ \forall x,y\in(a,b),\forall\lambda\in[0,1]: f(\lambda x+(1-\lambda)y)\geq \lambda f(x) + (1-\lambda)f(y)\,\! $).

Relativní entropie

Kullback-Leibler divergence (distance)/relativní entropie pro odhad pravděpodobnostního rozdělení $ q\,\! $ a skutečné rozdělení $ p\,\! $ nad stejným sample space $ \Omega\,\! $ je:

$ D(p||q) = \sum_{x\in\Omega} p(x)\log_2\left(\frac{p(x)}{q(x)}\right) = E_p \log_2\left(\frac{p(x)}{q(x)}\right)\,\! $

Tato funkce není symetrická a nesplňuje trojúhelníkovou nerovnost, ale je dobré jí uvažovat jako vzdálenost. Počet bitů pro zakódování dat z $ p\,\! $, používáme-li $ q\,\! $, lze vyjádřit jako $ H(p) + D(p||q)\,\! $.

Vlastnosti relativní entropie

Informační nerovnost:

$ D(p||q)\geq 0\,\! $

Důkaz plyne z Jensenovy nerovnosti -- pro $ p(x)\,\! $, náhodnou veličinu $ X\,\! $ on $ \Omega\,\! $ a konvexní funkci $ f\,\! $ platí, že $ f\left(\sum_{x\in\Omega} p(x)\cdot x\right) \leq \sum_{x\in\Omega} p(x) f(x)\,\! $. Jensenovu nerovnost lze ověřit indukcí nad $ |\Omega|\,\! $ za použití definice konvexity funkce. Pak stačí vzít $ 0 = -\log 1 = -\log \sum_{x\in\Omega} q(x) = -\log \sum_{x\in\Omega} p(x)\frac{q(x)}{p(x)} $ a použít Jensenovu nerovnost.

Dále platí:

  • Platí nerovnost sumy logaritmů pro $ r_i,s_i\geq 0\,\! $: $ \sum_{i=1}^n (r_i\log\left(\frac{r_i}{s_i}\right))\leq (\sum_{i=1}^n r_i)\cdot\log\left(\frac{\sum_{i=1}^n r_i}{\sum_{i=1}^n s_i}\right)\,\! $. Z toho $ D(p||q)\,\! $ je konvexní v $ p,q\,\! $.
  • Pro rozdělení $ p\,\! $ a rovnoměrné rozdělení $ u\,\! $ nad $ \Omega\,\! $ platí: $ H(p)\leq\log_2 |\Omega|\,\! $, $ H(X) = \log_2 |\Omega| - D(p||u)\,\! $, $ H(p)\,\! $ je konkávní.

Vzájmená informace

Vzájemná informace dvou náhodných veličin $ X, Y\,\! $ je:

$ I(X,Y) = D(p(x,y) || p(x)p(y))\,\! $

Měří, kolik v průměru $ Y\,\! $ přispívá k zjednodušení predikce $ X\,\! $ (o kolik bitů se sníží entropie), nebo o kolik se $ p(x,y)\,\! $ odchyluje od $ p(x)\cdot p(y)\,\! $. Alternativní zápis je:

$ I(X,Y) = \sum_{x\in\Omega}\sum_{y\in\Psi} p(x,y)\log_2\left(\frac{p(x,y)}{p(x)\cdot p(y)}\right)\,\! $

Platí:

$ I(X,Y) = H(X) - H(X|Y) = H(Y) - H(Y|X)\,\! $

Protože $ p(x,y)/p(x) $ v předchozím vzorci se dá díky definici podmíněné pravděpodobnosti vyčlenit jako $ -H(Y|X) $, zbývající $ 1/p(x) $ se dá přepsat na rozdíl dvou logartimů a $ \sum_{y\in\Psi} p(x,y) = p(x) $ z něj dá $ H(X) $.

Další vlastnosti:

  • $ I(X,Y) = H(X) + H(Y) - H(X,Y)\,\! $
  • $ I(X,X) = H(X)\,\! $ (protože $ H(X|X) = 0\,\! $)
  • $ I(X,Y) = I(Y,X)\,\! $
  • $ I(X,Y)\geq 0\,\! $ (z Informační nerovnosti)

Křížová entropie

Odhadujeme skutečné rozdělení pravděpodobnosti $ r\,\! $ rozdělením $ p\,\! $ (na základě vzorku pozorování $ T\,\! $) a potřebujeme znát přesnost aproximace. Nemáme skutečné $ p\,\! $, takže ho simulujeme další množinou vzorků $ T'\,\! $ (s rozdělením $ p'\,\! $). Křížová entropie se pak vypočítá jako:

$ H_{p'}(p) = -\sum_{x\in\Omega} p'(x)\log_2 p(x)\,\! $

V praxi se více používá podmíněná křížová entropie. Testujeme rozdělení $ p(y|x)\,\! $ proti $ p'(x,y)\,\! $ (z nezávislých dat $ T'\,\! $):

$ H_{p'}(p) = -\mathop{\sum_{y\in\Psi}}_{x\in\Omega} p'(x,y)\log_2 p(y|x) = -\frac{1}{|T'|}\sum_{i=1}^{|T'|}\log_2 p(y_i|x_i)\,\! $

Křížová entropie $ H_{p'}(p)\,\! $ může být nižší, vyšší než i rovna entropii odhadu rozdělení $ H(p)\,\! $. Používá se k porovnávání odhadů -- lepší odhad má nižší křížovou entropii na testovacích datech.

Bayesovské učení

Bayesovské učení je jiný přístup k odhadování pravděpodobnosti jevů než na základě frekvence výskytu: používáme navíc apriorní předpoklad (např. předpoklad známého rozdělení náhodné veličiny apod.), který na základě pozorovaných dat upravujeme. Hledaný jev (hypotéza) přitom může být např. klasifikační funkce strojového učení nebo nějaký neznámý parametr pravděpodobnostního modelu. Úplně přesně odpovídá Zlatému pravidlu NLP.

Definujeme:

  • $ p(h)\,\; $ -- apriorní pravděpodobnost jevu $ h $. Toto je náš apriorní předpoklad, nezávisí na datech.
  • $ p(D)\,\; $ -- pravděpodobnost výskytu pozorovaných dat $ D $ bez znalosti pravděpodobnosti jevů (naštestí díky Zlatému pravidlu není moc potřeba ji znát).
  • $ p(D|h)\,\; $ -- podmíněná pravděpodobnost výskytu dat $ D $, nastal-li jev $ h $.
  • $ p(h|D)\,\; $ -- aposteriorní pravděpodobnost, pravděpodobnost jevu $ h $ za předpokladu, že máme pozorovaná data $ D $.

Zajímá nás právě $ p(h|D)\,\; $. Z Bayesovy věty plyne, že $ p(h|D) = \frac{p(D|h)p(h)}{p(D)}\,\; $.

Hledáme-li jev s maximální aposteriorní pravděpodobností (maximální aposteriorní hypotézu), pak můžeme podle Zlatého pravidla použít vzorec:

$ h_{MAP}=\arg\max_{h\in H} p(D|h)p(h)\,\; $

Pokud jsou apriorní pravděpodobnosti všech jevů stejné (tj. apriorní předpoklad je rovnoměrné rozdělení), pak maximálně vhodná hypotéza (maximum likelihood hypothesis) je:

$ h_{ML}=\arg\max_{h\in H} p(D|h)\,\; $

Bayesovské rozhodovací pravidlo (nebo optimální bayesovské rozhodnutí) velí vybrat právě $ h_{MAP}\,\; $ ze všech možných hypotéz.

Příklad

Mějme medicínský diagnostický test, který pro určité onemocnění vyjde pozitivně ($ \bullet $) nebo negativně ($ \circ $), a dva jevy (hypotézy) -- pacient buď má ($ h_{+}\,\; $) nebo nemá ($ h_{-}\,\; $) danou nemoc. Apriorní předpoklad je, že $ 0.8\%\,\; $ populace má tuto nemoc.

Testy mají omezenou spolehlivost:

platí $ h_{+}\,\; $ platí $ h_{-}\,\; $
pozitivní test ($ \circ $) 98% 3%
negativní test ($ \bullet $) 2% 97%

Potom u pacienta s pozitivním výsledkem testu (tj. pozorovaných dat $ D\,\; $) najdeme $ h_{MAP}\,\; $:

  1. pravděpodobnost, že tento pacient má danou nemoc je $ p(\bullet|h_{+})p(h_{+}) = 0.98 \cdot 0.008 = 0.0078\,\; $
  2. pravděpodobnost, že tento pacient nemá tuto nemoc je $ p(\bullet|h_{-})p(h_{-}) = 0.03 \cdot 0.992 = 0.0298\,\; $

A tedy $ h_{MAP} = h_{-}\,\; $. I když takto přesný test vyjde pozitivní, je u málo častého onemocnění velká šance, že jde o planý poplach. V praxi se proto testy opakují.

Vztah k učení založenému na konceptech

Mějme problém strojového učení, kdy hledané hypotézy $ h\in H\,\; $ představují funkce klasifikující data $ D\,\; $ a my chceme z nich vybrat tu nejlepší. Použijme bayesovské učení tímto brutálně neefektivním způsobem:

  1. Spočteme $ p(h|D) = \frac{p(D|h)p(h)}{p(D)}\,\; $ pro každé $ h\in H\,\; $.
  2. Najdeme $ h_{MAP} = \arg\max_{h\in H} p(h|D)\,\; $.

Předpokládejme, že žádná z hypotéz není pravděpodobnější než jiná (což typicky předpokládat musíme). Dále uvažujeme, že $ p(D|h)\,\; $ bude $ 1\,\; $, pokud klasifikace hypotézou $ h\,\; $ souhlasí s ohodnocením dat a $ 0\,\; $ jinak.

Odhady velikostí pravděpodobností dojdeme k tomu, že jakákoliv hypotéza, která je konzistentní s trénovacími daty (tj. tato funkce by trénovací data klasifikovala správně), je $ h_{MAP}\,\; $. Tedy mnoho algoritmů strojového učení, které takové hypotézy hledají, je efektivnější variantou bayesovského učení.

Souvislost s minimální délkou popisu

Bayesovské učení splňuje podmínku Occamovy břitvy, neboli minimální délky popisu (minimum descripton length), tedy nalezení co nejkratšího modelu $ h_{MDL}\,\; $ pro danou situaci. Platí totiž:

$ h_{MAP} = \mathrm{argmax}_{h\in H} p(D|h)p(h) = \mathrm{argmax}_{h\in H}\log_2 p(D|h) + \log_2 p(h) = $
$ h_{MAP} = \mathrm{argmin}_{h\in H} - \log_2 p(D|h) - \log_2 p(h) $

A to se dá interpretovat jako preference nejkratší hypotézy s ohledem na specifický systém reprezentace hypotéz a dat. Pokud označíme $ L_C(i)\,\; $ počet bitů potřebných k zakódování zprávy $ i\,\; $ v kódování $ C\,\; $, pak se dá vzorec přepsat jako:

$ h_{MAP} = \mathrm{argmin}_h L_{C_h}(h) + L_{C_{D|h}} (D|h) $

Použijeme-li optimální kódování prostoru hypotéz i dat s ohledem na hypotézu $ h $, pak $ h_{MAP} = h_{MDL}\,\; $.

Optimální bayesovská klasifikace

Ve strojovém učení často není třeba vybrat nejlepší hypotézu $ h_{MAP} $, ale postupně po jednom klasifikovat nové příklady z dat. Máme-li možné hodnoty $ y_j\in Y $, pak je bayesovská pravděpodobnost těcthto hodnot dána vztahem:

$ p(y_j|D,x) = \sum_{h_i\in H} p(y_j|h_i)p(h_i|D,x) $

Optimální bayesovská klasifikace (optimální bayesovské učení) je to $ y_j $, pro kterou je $ p(y_j|D,x)\,\; $ maximální, tedy $ \mathrm{argmax}\,\; $.

Tato metoda maximalizuje pravděpodobnost, že nová data budou klasifikována správně, jsou-li dána trénovací data, prostor hypotéz a apriorních pravděpodobnosti.

Bayesův optimální klasifikátor poskytuje sice nejlepší možné výsledky z trénovacích dat, ale je výpočetně náročný. To motivuje použití Gibbsova algoritmu:

  1. Vybere se náhodně $ h\in H $, ale vzhledem k distribuci aposteriorních pravděpodobností nad $ H $.
  2. $ h $ se použije k predikci klasifikace nové instance.

Dá se dokázat, že klasifikační chyba Gibbsova algoritmu je menší než dvojnásobek chyby optimálního bayesovského učení.

Naive Bayes Classifier

Naivní bayesovský klasifikátor je rychlá a relativně úspěšná metoda strojového učení. Mějme data, jejichž instance lze popsat $ n\,\; $-ticí hodnot atributů $ a_i,\dots a_n\,\; $ a jejich klasifikaci, jež nabývá hodnot $ y_i \in Y\,\; $.

Naivní bayesovský klasifikátor předpokládá nezávislost hodnot jednotlivých atributů, tedy:

$ p(a_1,\dots,a_n|y) = \prod_{i=1}^n p(a_i|y)\,\; $

Ve výsledku z běžného bayesovského přístupu dostaneme:

$ y_{NBC} = \mathrm{argmax}_{y\in Y} p(y)\prod_{i=1}^n p(a_i|y) $ (a $ p(y)\,\; $ odhadneme jako relativní frekvence na trénovacích datech)

Je-li splněn předpoklad o podmíněné nezávislosti hodnot atributů, je $ y_{NBC} = y_{MAP}\,\; $. To sice v praxi splněno nebývá, ale přesto lze dosáhnout dobrých výsledků.

Hidden Markov Models

Skrytý Markovův model je užitečný prostředek k predikci dat na základě omezené historie předchozích výstupů. Dá se aplikovat např. na jazykové modelování při statistickém překladu nebo na morfologické značkování.

Markovův proces

Mějme posloupnost náhodných veličin $ \{X_i\}_{i=0}^T\,\; $ (obecně až do $ \infty\,\; $) a stavový prostor $ S = \{s_0,\dots,s_N\}\,\; $. Potom posloupnost $ \{X_i\}\,\; $ nazveme Markovův řetězec (proces), pokud splňuje Markovovu vlastnost:

$ P(X_{i+1}=s_j | X_i = s_i, X_{i-1}=s_{i-1}, \dots X_0 = s_0) = P(X_{i+1}=s_j | X_i = s_i ) \ \ \forall i\in\{0,\dots T\}\,\; $

Přitom musí pro každé $ i\in\{0,\dots T\} $ platit $ P(X_i = s_i, X_{i-1}=s_{i-1}, \dots, X_0 = i_0 )>0\,\; $. Mám tu tedy omezenou historii a rozdělení pravděpodobnosti přechodů z jednotlivých stavů se s časem nemění.

Formálně, abychom mohli mít závislost na více předchozích stavech, můžeme si nadefinovat nové stavy jako uspořádané $ n\,\; $-tice stavů původních (a nastavit pravděpodobnosti u nenavazujících na $ 0\,\; $). Takovému Markovovu procesu se říká Markovův proces $ n\,\; $-tého řádu. Máme tu vlastně aproximaci řetězového pravidla:

$ P(s_1,\dots,s_T) = \prod_{i=1}^T p(s_i|s_1,\dots,s_{i-1}) \approx \prod_{i=1}^T p(s_i|s_{i-n+1},\dots,s_{i-1})\,\; $

Markovův proces lze zapsat buď přechodovou maticí, kde na pozici $ i,j\,\; $ se nachází pravděpodobnost přechodu ze stavu $ s_i\,\; $ do $ s_j\,\; $, nebo stavovým diagramem -- grafem. Odpovídá to vlastně nedeterministickému konečnému automatu.

Skrytý Markovův Model

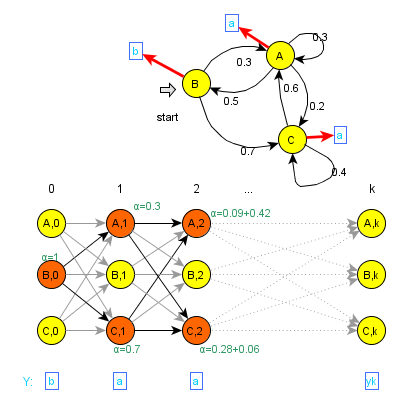
Skrytý Markovův model -- nejsložitější varianta

Nyní uvažujme složitější případ, kdy jednotlivé stavy Markovova procesu generují pozorovatelný výstup (znaky nějaké konečné abecedy), ale stavy samy a pravděpodobnosti přechodu nám jsou neznámé. Takové modely nazveme skryté Markovovy modely (HMM). Uvažuje se několik (postupně čím dál tím složitějších) variant:

  1. Každý z výstupních symbolů je generován jen v jednom stavu
  2. Různé stavy můžou generovat shodné symboly
  3. Generování symbolů se provádí ne ve stavech, ale při přechodu (tj. závisí na dvojicích stavů)
  4. Při každém přechodu mohou být s různou pravděpodobností vygenerovány různé symboly (tj. pro každou dvojici stavů mám rozdělení pravděpodobnosti výstupních symbolů)

Formálně se HMM definují jako pětice $ \langle S, s_0, Y, P_S, P_Y\rangle\,\; $, kde:

  • $ S = \{s_0, \dots , s_N\}\,\; $ je množina stavů, $ s_0\,\; $ je počáteční stav
  • $ Y = \{y_0,\dots , y_V\}\,\; $ je abeceda výstupních symbolů
  • $ P_S(s_j|s_i)\,\; $ je množina pravděpodobnostních rozdělení přechodů mezi stavy
  • $ P_Y(y_k|s_i,s_j)\,\; $ je množina rozdělení pravděpodobností výstupu jednotlivých symbolů abecedy pro každý přechod

HMM můžeme reprezentovat maticí přechodu a množinou $ |Y|\,\; $ matic, které pro každý symbol udávají pravděpodobnost jeho vygenerování při všech stavových přechodech.

Hlavní použití HMM je:

  • Spočtení pravděpodobnosti dané posloupnosti vygenerovaných symbolů
  • Spočtení nejpravděpodobnější sekvence stavů, která vygenerovala danou posloupnost symbolů

Trellis a forward/backward algoritmus

HMM a jeho rozvití do trellisu. Stavy, které mohly vygenerovat výstupní sekvenci, jsou vyznačeny barevně a opatřeny hodnotou α.

Uvažujme nyní HMM, kde se výstupní symboly generují ve stavech a každý stav generuje jeden symbol (ale více stavů může generovat shodné symboly)2. Pro spočtení pravděpodobnosti posloupnosti výstupních znaků $ Y, |Y|=k\,\; $ vytvoříme speciální graf -- trellis, který modeluje chování původního HMM.

Stavy trellisu odpovídají stavům HMM v každém kroku generování, tj. místo stavů $ s_0,s_1,\dots,s_N\,\; $ máme stavy $ s_{0,0},s_{1,0},\dots,s_{N,0},s_{0,1},\dots,s_{N,k-1} $. Pravděpodobnosti přechodů jsou vzaty z původního HMM. Uvažujeme ovšem jen stavy, které mohly vygenerovat sekvenci $ Y\,\; $, ostatní nejsou užitečné.

Navíc si pro každý nový stav stanovíme hodnotu $ \alpha\,\; $, která udává pravděpodobnost, že se HMM v daný čas nacházel v daném stavu, je-li dána posloupnost $ Y\,\; $. Ta se spočítá následovně:

$ \alpha(s_{\bullet,t+1}) = \sum_{s_i\Rightarrow y_i} P_S(s_{\bullet}|s_i)\alpha(s_{i,t})\,\; $ (pro nějaký stav $ s_{\bullet} \Rightarrow y_{i+1}\,\; $ a $ t \in \{0,\dots k-2\}\,\; $, symbol "$ \Rightarrow\,\; $" zde značí "generuje")

Potom pravděpodobnost posloupnosti $ Y\,\; $ je součet hodnot $ \alpha\,\; $ ve stavech odpovídajících poslednímu kroku, které mohly vygenerovat poslední symbol. Při praktickém výpočtu pravděpodobnosti $ Y\,\; $ stačí, abychom drželi v paměti dva kroky výpočtu, tj. maximálně dvojnásobek stavů, než měl původní HMM. Máme tedy algoritmus s výpočetní složitostí $ |S|^2|Y|\,\; $ a paměťovou složitostí $ 2|S|\,\; $, formálně nazývaný forward algoritmus.

Pro variantu HMM, kde se výstupní symboly emitují při přechodech, můžeme pracovat podobně, jen vzorec pro $ \alpha\,\; $ bude následující:

$ \alpha(s_{\bullet,t+1}) = \sum_{(s_i,s_{\bullet})\Rightarrow y_i} P_S(s_{\bullet}|s_i)P_Y(y_i|s_i,s_{\bullet})\alpha(s_{i,t})\,\; $

Je zřejmé, že takhle lze postupovat oběma směry (čímž dostáváme backward algoritmus). Při implementaci je třeba dát pozor na normalizaci, abychom nepočítali s příliš malými čísly a nedošlo k podtečení. Výhodné je např. počítat $ \alpha\,\; $ v logaritmech.

Viterbi

Uvažujme teď další problém nad HMM. Pro danou posloupnost výstupních symbolů $ Y,|Y|=k\,\; $ chceme najít nejpravděpodobnější sekvenci stavů $ S_{\mathrm{best}}\,\; $, která ji vygenerovala. Platí:

$ S_{\mathrm{best}} = \arg\max_{S} P(S|Y) = \arg\max_{S} P(S,Y)\,\; $

Protože $ P(Y)\,\; $ je dané a tedy fixované. Potom z Markovovy vlastnosti plyne:

$ S_{\mathrm{best}} = \arg\max_{S} P(S,Y) = \arg\max_{S} P(s_0,\dots,s_k,y_0,\dots,y_{k-1}) = \arg\max_{S} \prod_{i=0}^{k-1} P_S(s_{i+1}|s_i) P_Y(y_i|s_i,s_{i+1})\,\; $

Uvažujme opět trellis, kde místo hodnot $ \alpha\,\; $ budeme počítat hodnoty $ v\,\; $, udávající pravděpodobnost nejpravděpodobnější sekvence stavů, která v zavedla HMM v daný čas do daného stavu, je-li dáno $ Y\,\; $:

$ v(s_{\bullet,t+1}) = \max_{(s_i,s_{\bullet})\Rightarrow y_i} P_S(s_{\bullet}|s_i)P_Y(y_i|s_i,s_{\bullet})v(s_{i,t})\,\; $

Viterbiho algoritmus na základě této rekurentní rovnice postupně počítá $ v\,\; $ (tedy jde o dynamické programování) a v každém stavu trellisu si pamatuje odkaz na nejpravděpodobnějšího předchůdce. Po projití celé posloupnosti výstupních symbolů pak může zpětně získat nejpravděpodobnější posloupnost skrytých stavů. V tomto případě je už nutné trellis uchovávat v paměti.

Existuje i varianta Viterbiho algoritmu, která hledá $ n\,\; $ nejpravděpodobnějších posloupností skrytých stavů. Pro tu je třeba uchovávat v každém stavu trellisu $ n\,\; $ nejpravděpodobnějších předchůdců. Při průchodu zpět stále uchováváme $ n\,\; $ nejlepších kandidátů.

Samozřejmě i tady je třeba pamatovat na normalizace a je možné použít prořezávání (s prahovou hodnotou buď pro $ v\,\; $, nebo pro pravděpodobnost přechodu, nebo uchovávat jen daný počet stavů).

Baum-Welch

Dalším problémem na HMM je odhadnutí neznámých pravděpodobností $ P_S\,\; $ a $ P_Y\,\; $ na základě posloupnosti výstupních symbolů $ Y\,\; $, tj. spočtení $ \arg\max_{P_S,P_Y} P(Y|P_S,P_Y)\,\; $. Globální maximum efektivně nalézt neumíme, takže se musíme spokojit s lokálním.

K tomu se opět použije trellis a Baum-Welchův algoritmus, specifický typ EM-algoritmu (expectation-maximization). Ten postupuje následovně:

  1. Inicializuje $ P_S\,\; $ a $ P_Y\,\; $ na nějaké počáteční hodnoty
  2. Expectation (estimation) step: spočítá pravděpodobnost dat na základě původních odhadů $ P_S, P_Y\,\; $
    1. Spočítá forward pravděpodobnosti $ \alpha\,\; $ (tj. aplikuje forward algoritmus, ale v paměti drží celý trellis)
    2. Spočítá (obdobně) backward pravděpodobnosti $ \beta\,\; $
  3. Maximization step: spočítá nové odhady pravděpodobností $ P_S, P_Y\,\; $:
    1. Pro všechny dvojice stavů i generované symboly -- $ c(s_{\bullet},s_{\circ},y) = \sum_{i=0, (s_{\bullet},s_{\circ})\Rightarrow y}^{k-1} \alpha(s_{\bullet,i})P_S(s_{\circ}|s_{\bullet})P_Y(y|s_{\bullet},s_{\circ})\beta(s_{\circ,i+1})\,\; $
    2. Pro všechny dvojice stavů -- $ c(s_{\bullet},s_{\circ}) = \sum_{y\in Y} c(s_{\bullet},s_{\circ},y)\,\; $
    3. Pro všechny stavy -- $ c(s) = \sum_{s'\in S} c(s,s')\,\; $
    4. Nové pravděpodobnosti: $ P'_S(s'|s) = \frac{c(s,s')}{c(s)}\,\; $, $ P'_Y(y|s,s') = \frac{c(s,s',y)}{c(s,s')}\,\; $
  4. Opakuje počítání odhadů, dokud nezačne konvergovat.

I tady je třeba normalizovat, navíc pokud máme nějaké aspoň hrubé odhady pravděpodobností (hlavně $ P_Y\,\; $), výsledek bude mnohem lepší.

Algoritmy učení a zpracování, aplikace v lingvistice

Sem zřejmě patří něco z otázky o strojovém učení. Přidávám ještě dvě věci, které tam nejsou a v lingvistice se používají. Aplikace je možné vidět třeba v analýze jazyka.

EM-Algoritmus

Zdroj: Wikipedia, Manning/Schütze, Mitchell -- Tuetschek 22:13, 26 Aug 2010 (CEST)

EM (expectation-maximization) algoritmus je obecný postup iterativního odhadu neznámých parametrů nějakého modelu, který se používá např. v Baum-Welchově algoritmu z předchozí sekce.

Mějme pozorovaná data $ X = \{x_1,\dots,x_m\} $ nad nějakými jevy. Uvažujme ještě další, nepozorovaná data $ Z =\{z_1,\dots,z_m\} $ nad stejnými jevy. Ta lze považovat za náhodnou veličinu, potom celková data $ Y = X\cup Z $ jsou také náhodná veličina, jejíž rozdělení je určeno známými hodnotami $ X $ a rozdělením $ Z $.

Cílem EM algoritmu je maximalizace pravděpodobnosti výskytu trénovacích dat za daných parametrů $ E(\ln P(Y|\theta)) $ -- tím nalezneme parametry, které odpovídají pozorovaným datům. Používáme střední hodnotu, protože $ Y $ je náhodná veličina. Musíme tedy spočíst střední hodnotu přes její rozdělení, které je ale určeno parametry $ \theta $, jež neznáme. Proto definujeme rekurentní funkci, která počítá potřebnou střední hodnotu, má-li dány nějaké "předběžné" parametry $ \theta $:

$ Q(\theta'|\theta) = E(\ln P(Y|\theta')|\theta, X) $

Celý algoritmus pak postupuje iterací následujících dvou kroků, za předpokladu, že nastavíme počáteční $ \theta_0 $:

  • Expectation/Estimation -- spočítá se očekávaná hodnota $ Q(\theta_{n+1}|\theta_n) = E(\ln P(Y|\theta_{n+1})|\theta_n, X) $
  • Maximization -- vybere se takové $ \theta_{n+1} $, které maximalizuje funkci $ Q(\theta_{n+1}|\theta_n) $: $ \theta_{n+1} = \arg\max_{\theta_{n+1}} Q(\theta_{n+1}|\theta_n) $

Je-li funkce $ Q $ spojitá, je zaručeno, že EM algoritmus v každém kroku zvýší její hodnotu a bude konvergovat ke stacionárnímu bodu věrohodnostní funkce $ P(Y|\theta) $ (tj. k lokálnímu maximu).

Maximum Entropy

Tuto část jsem upravil ze své diplomky, takže je zkompilovaná z několika knih a článků. -- Tuetschek 22:13, 26 Aug 2010 (CEST)

Modely maximální entropie (maximum entropy, MaxEnt) jsou pro zpracování jazyka jedny z nejpoužívanějších. Jejich základní ideou je najít podmíněné rozdělení pravděpodobnosti, které má, za daných podmínek, maximální entropii. To odpovídá principu Occamovy břitvy -- najít co nejjednodušší popis na základě toho, co známe. Takový popis se co nejvíce blíží rovnoměrnému rozdělení a tedy má co nejvyšší entropii. Základní forma takového modelu, snažíme-li se předpovídat nějaký jev $ y\in Y\,\! $ na základě kontextu $ x\in X\,\! $, jako např. morfologický tag nějakého slova na základě vlastností okolního textu, vypadá následovně:

$ q_\theta(y|x) = \frac{\exp(\theta^T f(x,y))}{\sum_{y'\in Y} \exp(\theta^T f(x,y'))} \,\! $

Funkce $ f\,\! $ představuje $ N\,\! $-dimenzionální vektor rysů (jakýchkoli binárních klasifikací okolního textu) a $ \theta\,\! $ odpovídající vektor vah. Jmenovatel tohoto zlomku, tj. suma přes všechna možná ohodnocení, má v praxi pouze normalizační funkci.

Váhy modelu se potom odhadují tak, aby splnily podmínku maximální entropie, což je ekvivalentní minimalizaci relativní entropie našeho modelu $ q_\theta\,\! $ vzhledem k empirickému rozdělení pravděpodobnosti $ p\,\! $ pozorovanému na trénovacích datech (očekávaná frekvence výskytu jednotlivých vlastností), nebo maximalizaci jeho aposteriorní pravděpodobnosti (podmíněné pravděpodobnosti, jsou-li dána trénovací data), která se většinou popisuje pomocí logartimu věrohodnostní funkce:

$ \min_\theta D(p||q_\theta) = \min_\theta \sum_{y,x} p(y,x) \log\frac{p(y|x)}{q_\theta(y|x)} = \max_\theta L(\theta) = \max_\theta \sum_{y,x} p(y,x) \log q_\theta(y|x)\,\! $

Hledání maxima logaritmické věrohodnostní funkce se většinou provádí gradientovou metodou.


* ^ ad 1 V definicích entropie $ \Omega\,\! $ označuje množinu výstupů, ne vstupů náhodné veličiny $ X\,\! $.


Citováno z „http://wiki.matfyz.cz/index.php?title=Státnice_I3:_Stochastické_metody_a_jejich_aplikace_v_počítačové_lingvistice&oldid=19949“