Implementace databázových systémů/Komprese

okruhy 09/10: Komprese dat: predikce a modelování, reprezentace celých císel, obecné metody komprese, komprese textu. Huffmanovo kódování (statické, dynamické), aritmetické kódování, LZ algoritmy, komprese bitových map, rídkých matic.

okruhy 14/15: Komprese dat: modely textu, kódování, Huffmanovo kódování (statické, dynamické), aritmetické kódování, LZ algoritmy, komprese bitových map, rídkých matic, Burrows-Wheelerova transformace.

Modely textu

komprese textu

obecné typy redukce dat:

• ztrátová (nazývá se kompakce) - např. obraz, zvuk, video
• bezeztrátová (nazývá se komprese a je reverzibilní přes dekopresi)

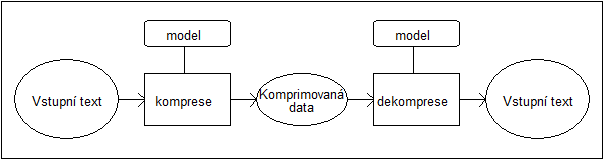
Proces komprese má 2 fáze:

• modelování (modely textu) - přiřazení pravděpodobností jednotkám textu (znaky nebo m-tice znaků pevné délky)
• kódování - transformace do nového kódu pomocí modelu

dělení modelů (💡 jako by slovníky):

• statické - model je statický pro všechny dokumenty (uložen jednou)
• semiadaptivní (polostatické) - ∀dokument má vlastní model (pošle se s dokumentem)
• dynamické (adaptivní) - oba algoritmy si model tvoří na základě již zpracovaných dat (musí se dekodovat od zacatku)

f: A → C⁺ je prosté kódové zobrazení znaků z abecedy A do prostoru slov v abecedě C

kódování

Zážitky ze zkoušek

komprese (2015, konzultace Kopecký) - pod kódováním bych já asi viděl obecnou problematiku kódování (tj. věci jako reprezentace nějaké posloupnosti znaků slovy nějaké abecedy, prefixovost, jednoznačnou dekódovatelnost, vztah mezi prefixovostí a jednoznačnou dekódovatelností, entropii, a podobně. To další jsou pak speciální případy s nějakými konkrétními vlastnostmi. Když budete umět Fibbonaciho/Eliasovy kódy jako speciální případy pro nekonečné množiny s nerovnoměrnou pravděpodobností výskytu znaků, určitě to nebude na škodu. komprese, obecně + komprese čísel (2008 Kopecký) - opět jsem neměl moc jasnou představu, kde je to využíváno - nicméně po lehkým naťuknutí jsem rovnou použil předchozí pohovor o indexaci dokumentů a správně řekl, že se to používá v tom invertovaném souboru pro kódování seznam těch dokumentů, kde se term vyskytuje. Pak jsem byl ještě poučen, že jak je ten seznam setřízen, tak se nekódují konkrétní čísla, ale přírustek od předchozího indexu.

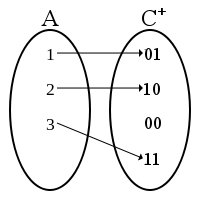
Kód K = (A,C,f), kde

• A = {a₁, ..., aₙ} je zdrojová abeceda, |A| = n
• C = {c₁, ..., cₘ} je cílová abeceda, |C| = m, obvykle C = {0,1}
• f: A → C⁺ je prosté kódové zobrazení znaků z abecedy A do prostoru slov v abecedě C.
• vlastnosti:
  • jednoznačně dekódovatelný - ∀zakódovaný (cílový) řetěz Y ∃ max. 1 zdrojový řetěz X že f(X) = Y.
  • prefixový - jednotliva kodova slova nejsou prefixem zadneho jineho slova
    • 💡 prefixový ⇒ jednoznačně dekódovatelný (opačně neplatí)

Entropie (míra informace) znaku ai v textu je rovna hodnotě E(aᵢ) = -log( "pst výskytu znaku aᵢ v textu" ) bitů.

• 💡 tj. "obrácená hodnota" - čím je znak častější tím menší má entropii = tím méně informace nese (tím menší počet bitů je potřeba na její reprezentaci)
• 💡 použítí viz: IDF/ITF

• prům. entropie 1 znaku: AE(A) = -Σ ("pst výskytu znaku ai v textu") log( "pst výskytu znaku aᵢ v textu" )
  • očekávaná délka 1 znaku přes ∀znaky a jejich psti
• entropie zprávy: E(A) = E(a₁...aₖ) = -Σ log( "pst výskytu znaku aᵢ v textu" )
  • 💡 tj. součet entropií znaků ve zprávě
  • platí že délka zakódované zprávy je |f(A)| > E(A)
  • redundance: R = |f(A)| - E(A)

speciální případy pro nekonečné množiny s nerovnoměrnou pravděpodobností výskytu znaků

Fibonacciho kody Zalozeno na fibonacciho cislech radu >=2 (např. při řádu 4, se Fib. číslo Fₙ = Fₙ₋₁ + Fₙ₋₂ + Fₙ₋₃ + Fₙ₋₄). Cislo se rozdeli hladovou metodou na scitance v podobe fibonacciho cisel. Ty se seradi od nejmensiho po nejvetsi, zapisi formou '1' je, '0' neni scitanec a zakonci se jednickou navic. pr. (fib cisla 1,2,3,5,8,13,21) 1 -> 11, 2 -> 011, 3 ->0011, 4 -> 1011, 12-> 101011, 32 ->00101011 prosty binarni zapis by byl sice kratsi, ale neodlisitelny. Tady mi dve jednicky delaji jasny konec znaku. (pokud se vyskytují dvě jedničky za sebou někde jinde, je možné je nahradit vyšším Fibonacciho číslem, pokud postupuju při určování jedniček od nejvyššího čísla, tak se mi to nestane) Eliášovy kódy řada kódování, které mají různé vlstanosti alfa kód (unární) – n-1 nul a na konci jednička, dekódovatelné, ale velmi dlouhé kódy beta kód (binární) – klasické binární kódování, krátké kódy, ale nedekódovatelné modifikovaný beta kód – stejně jako beta kód, ale bez úvodní jedničky theta kód – speciální znak pro rozlišení konce kódu gama kód – modifikovaný beta kód je obalený alfa kódem délky tohoto kódu – např. 37, v binárním kódu 100101, v modifikovaném beta kódu 00101, v gama kódu 00000100011 jednička na liché pozici určuje konec znaku v textu (krátké kódy + dekódovatelný) modifikovaný gama kód – na začátku má alfa kód délky modifikovaného beta kódu a za ním modifikovaný betakód 00000100101 není regulární (asi, že je potřeba dekódovat zprávu vždy odzačátku) delta kód – obdoba modifikovaného gama kódu, ale místo alfa kódu délky využívá gama kódu délky 0100100101, kde 01001 je gama kód pro 6 (délka beta(37)) omega kód – pro velmi velká čísla – posloupnost beta kódů zakončená nulou B₀,B₁,...,Bₖ,0 – Bₖ je binární zápis slova, Bᵢ₋₁ je binárním vyjádřením délky slova Bᵢ znižené o 1, velikost B₀ je 2 př: 37: 101011001010 0010 (1), 01100 (2), 01110 (3) nula na konci kódu je příznak toho, že při dekódování, pokud načtu první znak nulu, znamená to, že poslední přečtená část byla Bₖ a ne nějaké Bᵢ, i<k) kódování čísel se používá například při indexaci dokumentů, kdy mám invertovaný soubor, kde je index termů a každý term má seznam ID dokumentů, ve kterých se vyskytuje (pro urychlení vyhodnocování dotazů je tento seznam setřízen – tyhle čísla se pak kódují nějakým prefixovým kódem. Optimalizace, využívá toho, že menší čísla mají kratší kódy – místo jednotlivých ID se kódují pouze přírustky ID (tzn. mám-li seznam 2,8,13,15 – tak se kódují čísla 2, 6, 5, 2) Slajdy k OZD II (od slajdu 21) (Fibonacciho, Eliasovy kódy, fázování)

Znakové

Huffmanovo kódování (statické, dynamické) (🎓🎓🎓)

Huffmanovo k. se pouziva v poslední fázi u
JPEG MP3,...

StatickyHuffman(EMA MELE MASO)
seřadíme podle vyskytu, spojováním uzlů podle nejmenší četnosti zleva vytváříme binární strom

Zážitky ze zkoušek

Huffmanovo kódování - statické, dynamické (2015, Holubová) - Hned na zacatku mi bylo receno, ze se mam zamerit na dynamicke H. kodovani. Mel jsem cokoliv zakodovat a dekodovat. Huffmanovo kódování (2009) - stručně jsem popsal a nakreslil příklad k statické verzi, popsal jsem jak funguje dynamická, jak se mění strom atd. Huffmanovo kódovanie (2008, Galamboš) - toto som vedel, takže sa v tom moc nevŕtal

Staticke Huffmanovo kodovaní

Kodování

1. Spočítáme frekvence výskytů symbolů (včetně mezer).
2. Seřadíme znaky od nejmenší frekvence.
3. Spojováním dvojic zleva vytváříme strom. Nové vrcholy zařazujeme do řady (co nejvíce doprava).
4. Levé hrany jsou 0, pravé 1.

• výsledný strom se nazývá Huffmanův, výsledný kód je prefixový
• místo pravděpodobností můžeme použít i četnosti znaku, ohodnocení hran stromu pomocí 0 a 1 je konvencí (je tudíž možno použít i ohodnocení opačné)
• Huffmanuv i Shannon-Fanův kód je možné generovat v čase $ O(n) $

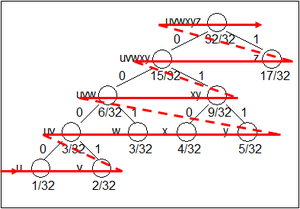
Dynamické (Adaptivní) Huffmanovo kódování

Sourozenecké pravidlo stromu: ∀ uzel má sourozence a četnosti v uspořádání podle červené šipky neklesají

• strom reorganizován podle toho, jak se mění pravděpodobnosti v průběhu kódování (tj. poruší se sourozenecké pravidlo)
• nepředpokládají se žádné informace o pravděpodobnostech zdrojových jednotek

FGK (Faller, Galagher, Knuth)

Dynamické kodovani

dekódování

Init: Začínáme se stromem s 1 vrcholem (speciální). Read: Načteme a najdeme znak ve stromu. Code: Na výstup vypisujeme čísla na hranách (0 vlevo, 1 vpravo). Není ve stromu⇒jdeme do speciálního vrcholu a pak vypíšeme znak na výstup. FixTree: Pokud znak ve stromu není, přidáme ho a aktualizujeme frekvence postupně až do kořene: Kontrolujeme zda ve stromu ve směru doprava nahoru není vrchol s menší frekvencí než je nová hodnota aktualizovaného. Pokud ano, vezmeme poslední takový a přehodíme ho s aktualizovaným (celé podstromy).

Init: Začínáme se stromem s 1 vrcholem (speciální - ? nebo NYT). Read: Čteme bity a podle nich hledáme ve stromě. DeCode: Pokud dojdeme do listu s písmenem, vypíšeme ho. FixTree: Dojdeme-li do speciálního vrcholu, načteme znak ze vstupu. Znak vypíšeme. Znak přidáme do stromu stejně jako při kódování.

• speciální vrchol se značí ? nebo NYT
• první definice symbolů abecedy se kódují nějakým základním prefixovým kódem
• dosahuje mensi (lepsi) delky kodoveho slova oproti staticke verzi

příklad kódování "aa bb" (dekódování prakticky stejné):

kódujeme zprávu "aa bb" 0. začneme stromem s jedním speciálním vrcholem ?(0) 1. kódujeme první znak zprávy a, vypíšeme kód spec.uzlu ? (prázdný řetězec) následovaný definicí znaku a, vložíme do stromu a aktualizujeme frekvence ve stromu Input: aa bb Output: a OutBin: 000 (1) 0/ \1 ?(0) a(1) 2. kódujeme další a, pouze vypíšeme jeho kód a aktualizujeme frekvence ve stromu Input: aa bb Output: a1 OutBin: 0001 (2) 0/ \1 ?(0) a(2) 3. kódujeme "mezeru", vypíšeme kód spec.uzlu ? (0) a definici znaku "mezera", vložíme do stromu a aktualizujeme frekvence ve stromu (žádné výměny nejsou potřeba) Input: aa_bb Output: a10_ OutBin: 00010001 (3) 0/ \1 (1) a(2) 0/ \1 ?(0) _(1) 4. kódujeme b, vypíšeme kód ? (00) a definici b, vložíme do stromu a aktualizujeme frekvence ve stromu (žádné výměny nejsou potřeba) Input: aa bb Output: a10 00b OutBin: 0001000100010 (4) 0/ \1 (2) a(2) 0/ \1 (1) _(1) 0/ \1 ?(0) b(1) 5. kódujeme další b, vypíšeme kód b a aktualizujeme frekvence ve stromu -> porušíme sourozeneckou vlastnost, musíme prohodit uzly na úrovni před kořenem a dokončíme aktualizaci frekvencí Input: aa bb Output: a10 00b001 OutBin: 0001000100010001 (4) 0/ \1 (2) a(2) 0/ \1 (1) _(1) 0/ \1 ?(0) b(2) ⇒ (4) 0/ \1 (3) a(2) 0/ \1 (1) b(2) 0/ \1 ?(0) _(1) ⇒ (5) 0/ \1 a(2) (3) 0/ \1 (1) b(2) 0/ \1  ?(0) _(1)

💡 Λ (Vitter)
- složitější úprava FGK s těmito vlastnostmi: počet výměn podstromů je nejvýše $ 1 $, přidá se escape sekvenci pro první výskyt nového znaku minimalizuje nejen $ \sum^n_{i=1} d[i] . p[i] $ ale i $ \sum^n _{i=1} d[i] $ a $ max_i d[i] $ $ AL_{HD} ≤ AL_{HS} + 1 $ (nejlepší hodnota mezi dynamickými Huffmanovými metodami)

💡 je optimální pro pravděpodobnosti výskytů znaků, které jsou mocninami 1/2.

aritmeticky zakodovat "JUJ!":
abeceda = {J,U,!} Pᵢ ={1/2, 1/4 , 1/4} 0|---J---|1/2----------U----|(1/2+1/4) -------------!---|1 0|---J---|1/4----------U----|(1/4+1/8) -------------!---|1/2 1/4|---J---|(1/4+1/16)---U----|(1/4+1/16+1/8+1/32) ---!---|(1/4+1/8) <1/4+1/8+1/16+1/32; 1/4+1/8> =bin <1/4+1/8+1/16+1/32; 1/4+1/8>

Aritmetické kódování

Diagram ukazující dekódování čísla 0.538 (kruhová tečka) pro ukázkový model. Oblast je rozdělená do podoblastí úměrně k četnostem symbolů, potom je podoblast obsahující tečku postupně rozdělen stejným způsobem.

vyjadruje kod jako interval z ⟨0;1).

Komprese: rozdelim interval ⟨0;1) na useky odpovidajici relativnim cetnostem jednotlivych znaku. Pri kodovani znaku se z intervalu ⟨0;1) "stane" interval ⟨x;y) odpovidajici kodovanemu znaku. Tento interval se pote vezme jako jednotkovy do dalsi iterace.

Reprezentujeme-li interval dvojici(L,S), kde L je dolni mez intervalu a S jeho delka, postupny vyvoj techto velicin muzeme vyjadrit takto:

L := L + S. cpᵢ

S := S . pᵢ

kde pᵢ je pravdepodobnost vyskytu kodovaneho znaku a cpᵢ = Σⁱⱼ₌₁ pⱼ neboli kumulovana pst. Pocatecni nastaveni je L=0 a S=1

Dekomprese: rozdelim interval ⟨0;1) na useky odpovidajici relativnim cetnostem jednotlivych znaku. Znak intervalu, ktery obsahuje kodovy interval dam na vystup a v tomto intervalu dale hledam.

Nevyhody: je treba aritmetiky velke presnosti, behem kodovani neni vystup – oboje lze ošetřit tím, že jakmile jsou známé první bity, tak se odešlou na výstup a dál se pokračuje se zbylým intervalem, který se jakoby posune o řád níž (např. pokud vím, že je interval [0; 0,001) v bitovém kódování, tak výsledný kód bude určitě vypadat ⟨0,00???; 0,00???))

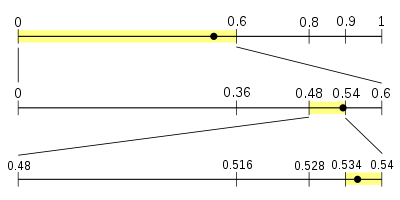
Priklad: Mame abecedu {a,b,c,d} s pravdepodobnostmi 1/2, 1/4, 1/8 a 1/8 a kodujeme "abc".

λ -> ⟨0;1)  
'a' - ⟨0;1) -> ⟨0;1/2)
'b' - ⟨0;1/2) -> ⟨1/4;3/8)
'c' - ⟨1/4;3/8)-> ⟨25/64; 26/64)

kód není prefixový ⇒ je třeba nějaký speciální znak pro odlišení konce kódu

oproti Huffmanovu kódování výhodné zejména pokud jeden znak je mnohem pravděpodobnější než ostatní

další zdroje
viz wen:Arithmetic coding Slajdy k OZD II (od slajdu 47) Dokumenty k DIS (myslím, že v posledním kroku příkladu je chyba)

Slovníkové metody

Kompresni algoritmy vytvareji pri sve praci slovnik, ktery pouzivaji ke kodovani vstupu. Vsechny metody jsou adaptivni, pri cteni kodu vytvari slovnik a zaroven taky generuji vysledny kod. Jsou kodovany "fraze" (shluky znaku nebo slova), cislovany ve slovniku od nuly.

Existuji dve zakladni kategorie:

1. organizujici slova prirozeneho jazyka (BSTW)
2. organizujici retezce (LZ*)

LZ algoritmy

Zážitky ze zkoušek

Komprese PNG a GIF (2012, Grafika, Zara) - Nejhorsi otazku sem si nechal na konec...tuhle sem absolutne nemel pripravenou, navic ji zkousel Zara Snazil sem se co nejdyl mluvit o obecnych metodach komprese obrazu ( RLE, Huffman, LZ77, LZW, Aritmeticke kodovani, Transformace obrazu ) ...to me ale Zara brzo zarazil ze to moc nesouvisi s tim na co se me ptaji at zacnu byt konretnejsi Tak sem otocil papir a tam sem mel par strohych poznamek o PNG a GIF formatech Kdyz sem to zacal komentovat tak me Zara prerusil at je spis vzajemne porovnam kdyz o nich mluvim. Co konkretne ho zajimalo: oba bezeztratove, LZ77 vs LZW, ze oba pouzivaji progresivni metodu zobrazeni, Proc muze mit PNG lepsi kompresni pomer nez GIF kdyz GIF pouziva modernejsi LZW oproti LZ77 ( odpoved ze LZ77 muze byt lepsi nez LZW na nekterych vstupech protoze je to uplne neco jinyho se mu moc nelibila...spravna odpoved je podle Zary ze tam je lepsi prediktor) No casto sem tady tipoval, hodne sem toho nevedel, parkrat me Zara poucil jak ze to vlastne je...celkem bida, ale mel sem pocit ze k vyhazovu sem mel jeste furt nejakou rezervu

LZW - Posíláme jen odkaz do slovníku (na začátku je v něm abeceda)

Komprese: pocatecnimi frazemi jsou jednotlive znaky. V kazdem kroku se najde nejdelsi fraze ve slovniku shodna se vstupem a jeji kod se zapise. Nova fraze vznika pridanim dalsiho znaku na konec akt. pouzite fraze.

pr. vstup ababababa

• poc. tabulka:

	fraze   a   b
	cislo   0   1

• chod alg.

kod   | slovník:
      | 0 a
      | 1 b
a   0 | 2 ab
b   1 | 3 ba
ab  2 | 4 aba
aba 4 | 5 abab
ba  3

Dekomprese: zacina se tak jako u komprese se slovnikem, ve kterem jsou pouze znaky. Nova fraze se tvori z predchozi plus prvniho pismena aktualni (je mozne, aby "nova" fraze sla hned na vystup - jeji zacatek znam - je z predchozi a posledni pismeno bude shodne s prvnim.

• Komprese i dekomprese vytvori stejny slovnik, používá se v GIF

LZ77 - Okénka (posíláme 3 údaje)

• na jeho zakladu jsou postaveny komprimacni programy soucasnosti(zip, arj,...)
• metoda typu sliding window - posunuju vstupem okenko, pomoci ktereho i koduju. Delim ho na dve casti hledaci (az 7 znaku a vyhledove az 7 znaku). Zprava je kodovana trojicemi <a, l, c> a je posun od aktualni pozice zpet, l je delka jiz kodovane casti ktera se znovu pouzije a c je novy znak. Kazda trojice tak zakoduje nejmene jeden a nejvice 7 znaku.
• proč zrovna 7 – vejde se to tak akorát do 3 bitů a je to rychlé
• pr. EMA MELE MASO se zakoduje <0,0,E>, <0,0,M>, <0,0,A>, <0,0,MEZERA>, <3,1,E>, <0,0,L>, <2,1,MEZERA>, <5,1,A>, <0,0,S>, <0,0,O>,
• pužívá se v PNG

Dalsi algoritmy - existuje spousta variant LZ algoritmu (LZ78 – starší obdoba LZW, LZJ – variace na LZW, kde je omezena délka kódovaných řetězců,...)

další zdroje
Slajdy k OZD II (od slajdu 56) (LZ77, LZSS, LZ78, LZW a další)

Komprese bitových map

Identifier	HasInternet	Bitmaps
		Y	N
1	Yes	1	0
2	No	0	1
3	No	0	1
4	Unspecified	0	0
5	Yes	1	0

Bitmapy se používají jako indexy pro atributy s malými doménami (napr.: muž/žena, low/medium/high,...)

• velikost bitmapy se rovná počtu záznamů * velikost domény ⇒ rostou lineárně s databází
• dotazování se dělá pomocí bitových logických boolovských operací

Tato část je neúplná a potřebuje rozšířit. projít podle OZD1H

Komprese

Uvažujeme bitovou mapu, resp. její j-tý sloupec (i-tá pozice říká, že záznam i odpovídá určité j-té hodnotě, nebo např. že dokument i obsahuje term j)

Uvažujeme předpoklad, že existence bitu 1 nebo 0 je nezávislá (pravděpodobnost p, že je tam 0, (1-p), že je tam 1). Z bitového řetězce lze spočítat pravděpodobnost p.

Rozdělíme bitový řetězec na bloky délky k a pro všechny možné bloky vzhledem k umístění jedniček (2^k) vypočítáme jejich pravděpodobnost. Potom pomocí Huffmanova kódování přiřadíme jednotlivým blokům kódy, kterými zakódujeme bitový řetězec. Čím větší p a k, tím větší zisk komprese, ale při velkém k (> 10) exponenicálně narůstá slovník, což nemusí být v praxi použitelné.

Druhou možností je nekódovat bloky pevné délky, ale běhy nul, zakončené jedničkou – tj. 1, 01, 001, 0001, atd. až do pevně stanovené velikosti m (tj poslední blok bude m nul). Spočítáme pravděpodobnosti pro běhy s jedničkou: (p^j)(1-p) – j je počet nul, zbylá pravděpodobnost do 1 (100%) bude odpovídat běhu ze samých nul. A opět Huffmanovým kódováním přiřadím kódy. V tomto případě slovník roste s k pouze lineárně, ale je zase hodně závislý na pravděpodobnosti, že se na vyskytuje 0 (když se blíží k 1, pak je to velice výhodné, jinak zisk komprese klesá)

• pomocí Huffmanova kódování
  • kódováním posloupností pevné délky
  • kódování běhů (posloupnost nul ukončených jedničkou apod.)

Slajdy k OZD II (od slajdu 92)

Řídké matice

řídká matice obsahuje z velké většiny nuly (např. vektorový index - cca 90% nul), lze reprezentovat:

• naivně ve tvaru matice (příliš veliké a neefektivní) ( $ \vec{d} $ = [w₁, w₂, ... , w_k] )
• seznamem indexů, kde se nachází nenulová hodnota ( $ \vec{d} $ = [j₁:w_j1, j₂: w_j2, ... , j_k: w_jk] )
  • kontrukce posuny - matici rozdělit na řádky, vhodně posuneme řádky (zaznamenáme), složíme řádky (sečteme), zaznamenáme do kterého řádku políčko patří
  • viz: OZD II

Burrowsova-Wheelerova transformace
Vstup	Všechny rotace	Seřazení rotací	Výstup
^BANANA@	^BANANA@ @^BANANA A@^BANAN NA@^BANA ANA@^BAN NANA@^BA ANANA@^B BANANA@^	ANANA@^B ANA@^BAN A@^BANAN BANANA@^ NANA@^BA NA@^BANA ^BANANA@ @^BANANA	BNN^AA@A

Burrows-Wheelerova transformace (BWT) - Matice, permutace

Pomocný algoritmus pro změnu pořadí symbolů (permutaci), tak aby se dobře komprimoval (často vyskytující se symboly dá k sobě).

• používá se v bzip2

tranformace

• Ze vstupního řetězce (zakončeného symbolem EOF) vytvoří všechny jeho možné rotace.
• Tyto se dále klasicky seřadí.
• Ze seřazeného pole rotací původního řetězce se do výstupního zapíše postupně od počátku poslední symbol z každé rotace.

komprese - move-front jako BSTW akorát že inicializujeme slovník abecedou

BSTW

• metoda nenavazujici na LZ
• na zacatku prazdny slovnik, ukladaji se do nej cela slova, vzdy na zacatek. Za kazde slovo je poslan jeho index ve slovniku nebo cislo o jedna vyssi nez je pocet slov ve slovniku spolu s novym slovem. Po kazdem "pouziti" slova ze slovniku se to slovo presune na zacatek slovniku.
• Pr. kazdy sofsemista musi kazdy den bdit cely den
  • zakoduje se na : 1 kazdy 2 sofsemista 3 musi 3 (<--- ted uz znamena kazdy) 4 den 5 bdit 6 cely 3 (=den)

další zdroje
http://cs.wikipedia.org/wiki/Burrowsova-Wheelerova_transformace