TIN065 Prednáška 01
| Prednášky z Vyčísliteľnosti II |
| Obsah |
|---|
Na vyčísliteľnosti I sme mali 1-prevoditeľnosť: $ A\leq_1 B $ znamená, že existuje prostá ORF funkcia f, pre ktorú platí, že $ a \in A \Leftrightarrow f(a) \in B $. Okrem tejto prevoditeľnosti existuje množstvo ďalších - napríklad známa m-prevoditeľnosť, ktorá sa od 1-prevoditeľnosti líši tým, že nepožaduje, aby funkcia f bola prostá ($ \leq_m $), potom "truth table" prevoditeľnosť ($ \leq_{tt} $), "weak truth table" prevoditeľnosť ($ \leq_{wtt} $) a pre nás najzaujímavejšia turingovská prevoditeľnosť ($ \leq_{T} $). Prevoditeľnosť slúži na to, aby sme vedeli zistiť, či nejaký prvok je prvkom množiny A na základe toho, že vieme o nejakých prípadne iných prvkoch zistiť, či sú prvkami množiny B.
Truth table reducibility
$ A \leq_{tt} B $ znamená, že existuje ORF, ktorá každému $ x \in A $ priradí n-árnu boolovskú funkciu $ \alpha $ a tiež n-ticu bodov $ y_1, y_2, ..., y_n $ takých, že $ C_A(x) = true \Leftrightarrow x \in A \Leftrightarrow \alpha(C_B(y_1),C_B(y_2), \cdots, C_B(y_n)) = true $, kde $ C_A $ je charakteristická funkcia $ A $ a $ C_B $ je charakteristická funkcia $ B $. (Spomínaná ORF teda priradí každému $ x $ kód funkcie $ \alpha $ a hodnoty ypsilónov).
Priradenie funkcie $ \alpha $ ako aj premenných $ y_i $ je závislé na $ x $, takže pre rôzne $ x $ môžu byť rôzne $ \alpha $ aj $ y $. Pekné na funkcii $ \alpha $ je, že je definovaná všade a to nezávisle na množine $ B $, pretože to je boolovská funkcia. A boolovská funkcia sa dá zapísať pravdivostnou tabuľkou - odtiaľ názov "truth table" redukcia (poznámka: boolovských funkcií na $ n $ premenných je $ 2^{2^n} $). Príklad množín, ktoré sú na seba prevoditeľné, je $ \overline{K} $ a $ K $. K prvku $ x $ priradíme prvok $ x $ (ten istý) a $ \alpha $ bude negácia (poznámka: 1-previesť sa nám ale $ \overline{K} $ na $ K $ nepodarí). K tomuto môžeme vymyslieť nejaké obmedzenia, či už na $ n $ (takže sa spýtame na najviac $ n $ prvkov), prípadne na tvar funkcie $ \alpha $. Tým sa teraz nebudeme zaoberať. Tiež prevoditeľnosťou "weak truth table" sa budeme zaoberať až časom.
T-prevoditeľnosť
Čo nás bude zaujímať viac, je T-prevoditeľnosť. Budeme potrebovať orákulum - hypotetické zariadenie, ktoré odpovedá na otázky "Je $ y $ prvkom $ B $?". Prípadne si môžeme predstaviť, že máme orákulovu pásku, na ktorej je zapísaná charakteristická funkcia množiny B.
Neformálne: $ A \leq_T B $ ak existuje program, ktorý počíta charakteristickú funkciu množiny $ A $, pričom sa občas môže spýtať, či nejaké $ y $, ktoré počas svojej práce vypočíta, je prvkom množiny $ B $.
Keďže hovoríme o programe, zišiel by sa programovací jazyk. Prvá možnosť je použiť $ B $-ČRF. B-čiastočne rekurzívne funkcie sú také, ku ktorým okrem už známych základných funkcií (nula, nasledovník, projekcia) existuje aj ďalšia - a to práve charakteristická funkcia množiny $ B $, teda $ C_B $. Tá slúži na zistenie, či nejaký prvok je prvkom množiny $ B $. Takže B-ČRF sú rozdielne pre každé $ B $. Inak povedané: $ B $ je vlastne množinová premenná. Operátory ostávajú rovnaké ako pri obyčajných ČRF.
Definícia pre Pascal-like jazyk (nazvaný tiež aj B-pascal) je, že pridáme k programu funkciu is_in_B(x:integer):boolean, ktorá vráti $ true $ ak $ x $ je prvkom $ B $ a $ false $ ak $ x $ nie je prvkom $ B $. Táto funkcia si svoj výsledok zisťuje "iným spôsobom" - pýta sa, či už užívateľa alebo orákula.
Pre Turingov stroj si zasa môžeme zaviesť "orákulovu pásku", ktorú stroju pridáme (ako ďalšiu pásku), na ktorej bude mať $ C_B $ (takže napríklad na tejto páske na pozícii $ i $ bude $ 0 $, ak $ i \notin B $ a $ 1 $ ak $ i \in B $).
Chcelo by to ukázať, že všetky tieto možnosti zavedenia sú ekvivalentné.
To, že B-ČRF môžeme reprezentovať Turingovým strojom s orákulom alebo B-Pascalom je viac menej vidieť. Ukáže sa to rovnako ako pri obyčajných ČRF - sú vybudované induktívne. Opačným smerom použijeme mierne všeobecnejší postup.
Výpočtový strom
Predstavme si program P so vstupmi B (množina) a x (číslo): P(B, x). To, ako náš program počíta sa dá nakresliť do výpočtového stromu.
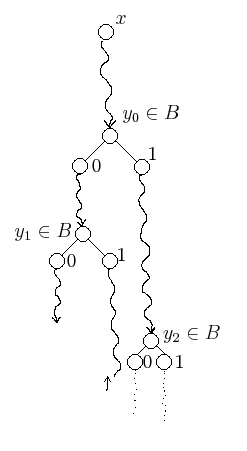
Tento strom zachytáva všetky možné scenáre behu programu pre ľubovoľný vstup $ x $ a ľubovoľnú množinu $ B $. Program dostane na vstupe $ x $ a množinu $ B $. Výpočet potom prebieha podobne ako výpočet bežného programu definovaného klasickou ČRF. Rozdiel je však v tom, že naviac je povolená operácia otázky. To znamená, že sa behom výpočtu je možné spýtať, či je nejaké $ y_i $ prvkom množiny $ B $. Podľa toho, aká bude odpoveď, sa je možné vo výpočte rozhodovať a následne sa vydať po ľavej či pravej vetve stromu. Týchto otázok je povolený neobmedzený počet. Výpočet môže dopadnúť rôzne. Buď skončí (na obrázku úplne ľavá vetva) alebo sa "zacyklí" (druhá vetva zľava). To, čo je pre nás dôležité je, že každý konečný výpočet sa skončí po konečnom počte krokov.
Kľúčové miesto
Množina konečných vetiev výpočtového stromu je rekurzívne spočítateľná. Nahliadne sa to tak, že prehľadávaním do šírky môžeme prejsť celý strom a tak efektívne vygenerovať všetky jeho konečné vetvy.
Tiež si môžeme vymyslieť aj rekurzívne spočítateľnú množinu $ W $, ktorá obsahuje štvorice $ <x, y, u, v> $, kde $ x $ je vstup programu, $ y $ je jeho výstup a $ u $ a $ v $ sú indexy konečných množín, ktoré vyrobíme tak, že keď ideme po vetve v strome od $ x $ k $ y $ (beží nám program), tak pri rozhodovaní sa, či $ y_i $ je prvkom množiny $ B $ uložíme $ y_i $ do množiny s indexom $ u $ ak $ y_i $ je prvkom množiny $ B $ a ak $ y_i $ nie je prvkom množiny $ B $, tak $ y_i $ uložíme do množiny s indexom $ v $. Indexy $ u $ a $ v $ na začiatku reprezentujú kód prázdnej množiny a postupne sa menia tak, že do odpovedajúcich množín pridávame práve rozhodované $ y_i $ podľa príslušnosti do $ B $. Ak v strome na obrázku pôjdeme stále vľavo, tak $ D_u $ (množina s indexom $ u $) bude prázdna a $ D_v $ bude obsahovať $ y_0 $ a $ y_1 $.
Potom platí: $ P(B, x) = y $ práve vtedy, keď $ (\exists u, v)(<x, y, u, v> \in W \and D_u \subset B \and D_v \subset \overline{B}) $.
A ešte sa na prednáške zopakovali definície, čo je to binárny reťazec (string) - konečná postupnosť núl a jedničiek. A tiež čo to znamená, že $ \sigma $ je začiatkom (prefixom) $ \tau $ (normálne to značíme $ \sigma $ \preceq $ \tau $, ale na tejto Wiki z technických dôvodov $ \sigma \leq \tau $). A ešte sme si povedali, že $ B $ a $ C_B $ stotožníme a že teda môžeme mať aj "prefix" množiny. A tiež, že množiny môžeme viac menej namapovať na reálne čísla medzi nulou a jednotkou. Problémy sú s číslami ako $ 0.1 $ a $ 0,01111111... $, ktoré sú rovnaké, ale predstavovali by inú množinu. A teda množín, s ktorými budeme pracovať, je nespočítateľne veľa.