Komplexní reprezentace polychromatických polí
Státnice - Fyzika NMgr: Seznam okruhů#4. Vlnová optika
- Monochromatická vlna: E(t)~exp(i(k∙r-ωt)) + c.c.. FT dá součet dvou δ-distribucí, jednu pro ω/2 a druhou pro -ω/2
- Polychromatická: E(t)=∑E0iexp(i(ki∙r-ωit)) + c.c. => FT dá součet více δ-distribucí
- Spojité spektrum: E(ω) = ∫RE(t) exp(-iωt) dt
Věnujme se nyní spojitému spektru: E(t) ∈ R => E(ω) = E*(-ω). Tímto se lze zbavit nefyzikálních záporných frekvencí (viz Němcova vlnová optika. Já u sebe ten sešit nyní nemám, takže si nejsem tak úplně jist, jak to je). Udělám poupravenou IFT a zavedu komplexní analytický signál: U(t) := ∫R+2E(ω) exp(iωt) dω.
K čemu tento komplexní analytický signál je dobrý?
- Zavedu koherenční funkci G(τ) := <U*(t) U(t+τ)>. Pozor: toto je souborová střední hodnota. Časová je limT→∞ 1/T ∫-T/2T/2 U*(t) U(t+τ) dt. Platí ergodický teorém: souborová střední hodnota je shodná s časovou, pokud máme stacionární vlnění.
Protože je G(0) = intentita světla, je vhodné ji normovat: g(τ) := G(τ) / G(0) = G(τ) / <U*(t) U(t)>. Pozn: G i g jsou komplexní. |g| ∈ <0;1>.
Lze zavést i prostorovou koherenci G(r1, r2, τ) := <U*(r1, t) U(r2, t+τ)> a g(r1, r2, τ) := G(r1, r2, τ) / .... Namísto tří teček se bere "střední intenzita v místech r1a r2", přesněji jejich geometrický průměr: g(r1, r2, τ) := G(r1, r2, τ) / √I(r1)I(r2). Připomenutí: I(r1) = G(r1, τ = 0). Pozn: G i g splňují vlnovou rovnici
Užití
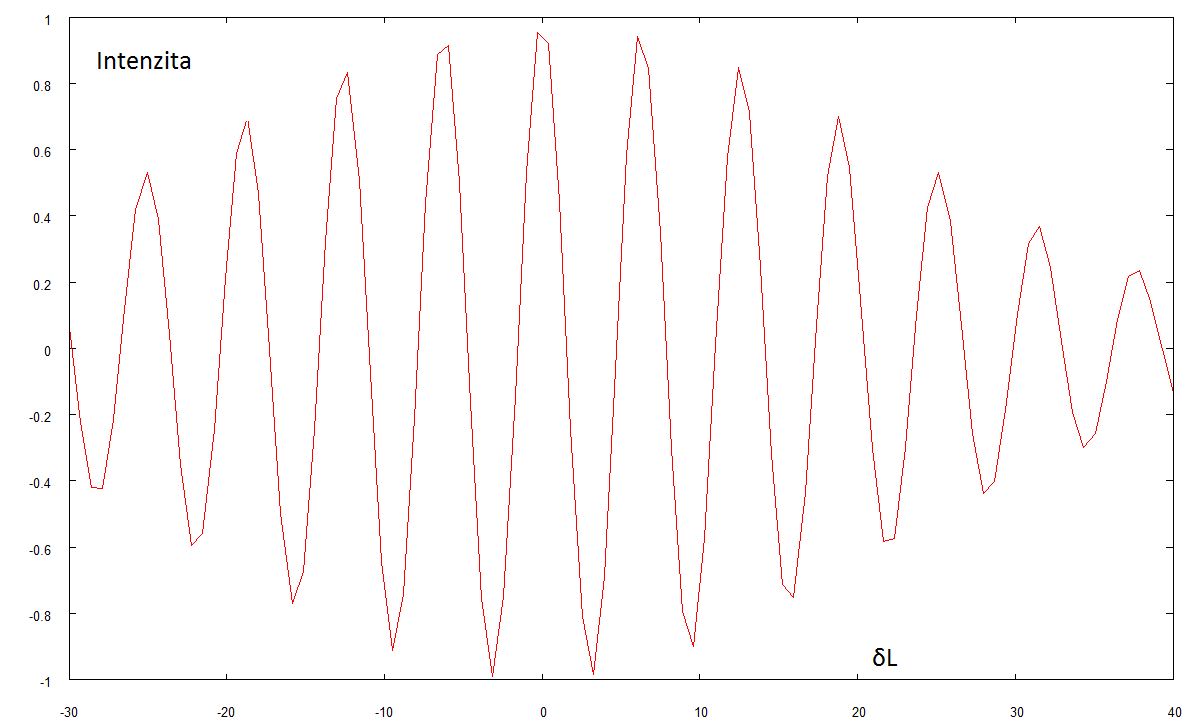
V Michelsonově inteferometru: chci viditelnost proužků V > 1/2. Intenzita světla dopadajícího do detektoru je (po chvilce počítání) dána jako I(x) = I0 + 2|g| cos(4π/λ |L1-L2|), kde I0 je intenzita vstupujícího světla, λ je vlnová délka použitého světla; L1 a L2 jsou délky jednotlivých ramen.
Od naměřené intenzity již byla odečtena intenzita vstupujícího světla (I0). Amplituda kmitů ~|g|, frekvence pak cos(4π/λ |L1-L2|). Ještě připomenu, že pro Lorentzovku i Gaussovku je τ~1/Δν, cτ = |L1-L2|