Formální základy databázové technologie/Relace
| Zážitky ze zkoušek |
|---|
|
Relační kalkul a relační algebra jsou prostředky relačního modelu dat pro manipulaci s daty
Obsah
Relační kalkuly (7×🎓)
| Zážitky ze zkoušek |
|---|
|
- neprocedurální jazyky
- relačně úplné, mohou obsahovat nebezpečná pravidla (⇒ silnější než RA)
- vychází z predikátové logiky 1. řádu (při dotazování) relační algebra ne
n-ticový relační kalkul (NRK)
| př(NRK): spojení (představení * kina):
|
|---|
|
| př(NRK): film, který dávají ve všech kinech, kde něco dávají (P $ = $ PŘEDSTAVENÍ)
|
|---|
|
- pracuje s daty na úrovni n-tic (prvků relace/řádků)
- Termy - n-ticové proměnné, jejich komponenty a konstanty
- Predikáty - jména relací a binární porovnávací predikáty θ (>, <, >=, <=, <>, =)
- Atomické formule R(x), x.A θ y.B, x.C θ 'konstanta', (θ je bin. porov. Predikát), R(t1,....tn) (R predikát, ti je term)
- Atomické formule NRK jsou formule NRK a formule složené z formuli pomocí &, ∨, ¬, ⇒, ⇔ jsou také NRK fle
- Kvantifikátory: ∃, ∀
doménový relační kalkul (DRK)
| př(DRK): spojení (P$ = $představení * k$ = $kina)
|
|---|
|
- Místo n-tic používá doménové proměnné (tj. atributy = sloupce), místo R.u se používá R(A:x, B:y,...), atribut:typ
- Termy - jednoduché proměnné, konstanty
- Atomické formule R(A1:T1, A2:T2, ...) - stejné jako u NRK
| další zdroje |
|---|
|
|
Relační algebry (3×🎓)
| Zážitky ze zkoušek |
|---|
|
| př.: herci z filmů v kině Mír
|
|---|
|
| př.: kdy je v RA mozne: $ \small(E_1 \times E_2)(selekce) = $ $ \small E_1(selekce) \times E_2 $ ?
|
|---|
|
je neprocedurální jazyk vysoké úrovně pro práci s relacemi v relačním datovém modelu
- 💡 neprocedurální, nicméně struktura výrazu navádí na pořadí a způsob vyhodnocení
- 💡 nemá nebezpečné výrazy
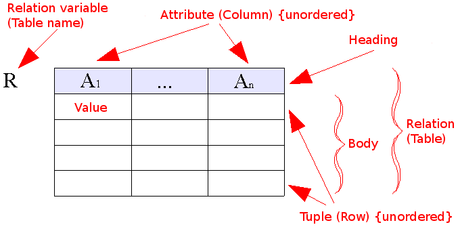
- Relace - má schema (atributy + domény, na pořadí atributů nezáleží ), obsahuje množinu n-tic (duplicity jsou eliminovány)
- Operace - vytvoří z vstupní relace/í výsledek jako novou relaci
- Minimálni množina 6 operací (tvoří rel.algebru AR):
- výběr () (select): - vrací relaci jejíž hodnoty atributů splňují danou podmínku, která může obsahovat jména atributů, konstanty, operátory prorovnávání a logické spojky
- projekce [] (project) - vrací relaci obsahující vybrané sloupce (duplicity jsou eliminovány)
- sjednocení $ \cup $ (union) - vstupní relace musí mít shodnou aritu (stejný počet atributů) a domény atributů musí být stejného typu (duplicity jsou eliminovány)
- množinový rozdíl $ \setminus $ (set difference) - musí platit stejné předpoklady jako u sjednocení
- kartézský součin $ \times $ (Cartesian product) - předpokládá se, že atributy vstupních relací jsou disjunktní (v opačném případě musí být provedeno přejmenování), v praxi mnohdy neproveditelné kvůli vysoké režii
- přejmenování $ ρ $ (rename)
- další odvozené operace
- Průnik $ \cup $ - dá se vyjádřit: $ R_1 \cap R_2 = (R_1 \cup R_2 \setminus (R_1 \setminus R_2))\setminus (R_2 \setminus R_1) $
- Přirozené spojení $ * $ (Natural join) - lze cca vyjádřit pomocí kartézského součinu, selekce a projekce: $ R * S = \left(\left(R \times S\right)\left(Rx = Sx\right)\right)[A \cup B] $
- Spojení přes výraz (normální je přes atributy) = inner join (zobecnění vnitřního spojení)
- Polospojení R <* S. Spojení s projekcí na schema relace, které je menší tj. R
- Levé/Pravé vnější spojení - ve spojení jsou zachovány všechny n-tice z levé/pravé/obou relací, pokud řádky vyhovují podmínkám spojení (v SQL jsou doplněné null, RA toto neumožňuje, jelikož je relačně úplná)
- 💡 Rozdíly mezi Joiny
- Dělení (÷) : Dělíme všechny představení Filmy(režisér=čáp).[jmeno_f]. Vrátí to ntici odpovídajícím všechem kinům, kde všechny filmy režíroval čáp (defakto to vydělí všechny stejný kina čápem a pokud je to jedna tak to vypíše)
- lze vyjádřit pomocí projekce, rozdílu a kartézského součinu: $ R \div S = R[A\setminus B] \setminus ((R[A\setminus B] \times S)\setminus R)[A\setminus B] $
- Dotazovací jazyk Relační algebry - jeden dotaz lze zapsat mnoha způsoby, toho se vyžívá v alg. optimalizaci dotazu
- Jednoduchý dotaz - lze vyjádřit pouze pomocí selekce, projekce a spojení (až 80%) - nejvíc optimalizovány
- Relační úplnost - pokud lze prostředky jazyka lze vyjádřit min.množinou operací $ A_{R} \{(), [ ], \cup, \setminus, \times, rename \} $
- Pozitivní relační algebra $ A_{RP} \{(), [ ], \cup, \times, rename \} $ - je fragment RA vzniklý odstraněním množinového rozdílu
- 💡odpovídá nerekurzivnímu DATALOGu (bez negace)
- Konstantní relace (relace co se nemění po dobu života DB) - např Číselník
| Příklad(srovnání RA, DRK, NRK) |
|---|
|
definujeme rel.schémata: FILM(JMENO_FILMU, JMENO_HERCE) HEREC(JMENO_HERCE, ROK_NAROZENI) Dotaz: Ve kterých filmech hráli všichni herci? RA: $ \small FILM \div HEREC[JMENO\_HERCE] $ NRK:$ ~ \small\{f.JMENO\_FILMU \;|\; \forall herec(HEREC(herec) \Rightarrow f(FILM(f) \wedge\; f.JMENO\_HERCE = herec.JMENO\_HERCE \;\wedge f.JMENO\_FILMU = film.JMENO\_FILMU))\} $ DRK: $ \small\{(f) | FILM(f)\wedge \forall h (HEREC(h) \Rightarrow FILM(f, h))\} $ |
| další zdroje |
|---|
|
|
Bezpečné výrazy (2×🎓)
| Zážitky ze zkoušek |
|---|
|
| bezpečné fle
|
|---|
|
volne proměnné - nejsou v zadnem kvantif. (např R(x)), vázané - jsou v nejakem kvantifikátoru (např: ∃xR(x))
Definujeme: výrazy dotazu $ \{x_1,...,x_k | A(x_1,...,x_k )\} $, $ A $ je formule DRK, databáze $ R* $, dom je doména pro $ R $, aktuální doména formule $ A $ $ adom(A) $ je množina hodnot z relací v $ A $ a konstant v $ A $.
Problém RK jsou nekonečné domény, které je potřeba omezit (aktuální doménou - adom), aby nedocházelo k nežádoucím jevům:
- Nekonečná odpověď v případě nekonečné $ dom $ (např. $ \{ x,y | x=y \} $ )
- situace, kdy TRUE ohodnocení volných proměnných není v DB (např. $ \{ x | ¬Employee(Name: x)\} $ )
- nekonečný výpočet (impl. vyhodnoceni kvantifikace na nekonečné $ dom $) (např. $ \{ x | ∀y R(x,...,y) \} $ kde y má nekon.doménu )
řešením jsou doménově nezávislé (definitní, určité) dotazy $ DRK^{ind} $
- tj.: nejsou definitní pokud pod ruznymi $ dom $ davaji ruzne vysledky
- bezpečná formule ⇒ je také doménově nezávislá (opačně to neplatí, dom.nezávislé jsou nadmnožinou bezpečných)
| další info |
|---|
|
další sémantiky (stejně silné), které uvedené problémy řeší:
$ DRK^{out}≅DRK^{lim}≅DRK^{ind} $ |
zjistit, zda je DRK výraz dom.nezávislý je nerozhodnutelný problém (∄program co zjisti jestli je dom.nezávislý) a tedy $ DRK^{ind} $ není rek.spočetný jazyk
máme ale jednoduchá syntaktická pravidla (třídu) která nám určují bezpečné formule (jsou podmnožinou dom.nezávislých):
Bezpečné formule DRK
| př: bezpečná pravidla DRK: |
|---|
|
| př: nebezpečná pravidla NRK
|
|---|
|
- nemají ∀
- ( $ ∀x~ φ(x) $ můžeme nahradit $ ¬∃x (¬φ(x)) $ )
- každá disjunkce $ \varphi_1 \or \varphi_2 \or ... $obsahuje stejné volné proměnné
- ( $ \varphi_1 \Rightarrow \varphi_2 $ tranformujeme na $ ¬\varphi_1\or\varphi_2 $ )
- každá konjunkce (maximální), $ φ \equiv φ_1∧...∧φ_r $má všechny volné proměnné omezené, tj. platí pro ni alespoň 1 z podmínek:
- (a) proměnná je volná v $ \varphi_i $co není negace ani binární porovnání
- (b) ∃$ \varphi_i\equiv x=a $, kde $ a $ je konstanta nebo omezená proměnná
- ¬ smí být pouze v konjunkcích z bodu 3
| další zdroje |
|---|
|
Bezpečné (safe) formule NRK
| syntaktická pravidla pro bezpečné výrazy v NRK (nebylo na přednášce) |
|---|
|
| př: nebezpečná pravidla Datalog
|
|---|
|
z přednášky:
z media:Datalog-unsafe_rules.PNG:
(ve všech připadech nekonečnost X splni pravidlo i když je R konečná relace) |
Bezpečné pravidla v Datalogu
- Omezená proměnná x v Datalogu je taková, která se vyskytuje v těle literálu L a pro jehož tělo platí:
- L je dán pravým predikátem, nebo
- pravý predikát - jméno zákl.db relace nebo jméno virtuální relace (prakticky EDB nebo levá strana IDB pravidla)
- L je x = a nebo a = x , kde a je konstanta nebo omezená proměnná
- L je dán pravým predikátem, nebo
Pravidlo je bezpečné pokud jsou ∀proměnné omezené.
Datalog má povolená pouze bezpečná pravidla a dále platí, že v hlavách jsou pouze jména virtuálních relací
- 💡 (ktere nejsou v EDB), tzn odvozováním nevytvářím další základní data
Ekvivalence dotazovacích jazyků
- NRK omezený na bezpečné výrazy je ekvivalentní $ A_{R} $ (relační algebře)
- Z toho plyne, že kalkulové jazyky lze realizovat pomocí $ A_{R} $, která je relativně dost silná (ale nemá na logiku 1. řádu - Datalog)
- DRK omezený na bezpečné výrazy je ekvivalentní $ A_{R} $
💡 DRK s doménově nezávislými výrazy je silnější než $ A_{R} $
- NRK omezený na bezpečné výrazy je ekvivalentní DRK omezenému na bezpečné výrazy
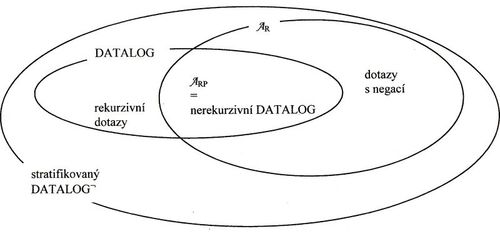
- Datalog je silnější než $ A_{RP} $ (pozitivní RA)
- Tranzitivní uzávěr (rekurze)
- V datalogu nelze vyjádřit rozdíl, proto není silnější než obyč RA
- Stratifikovaný Datalog¬ je silnější než $ A_{R} $
- tranzitivní uzávěr (rekurze)
- rozdíl lze vyjádřit pomocí negace
💡 Stratifikovaný nerekurzivní Datalog¬ je ekvivaletní $ A_{R} $
Relační úplnost (2×🎓)
| Zážitky ze zkoušek |
|---|
|
relačně úplný jazyk - má prostředky přímo realizovat všechny operace $ A_R $ ( tj. "minimalne tak silny jako RA" )
Relačně úplný je:
- NRK, DRK (s bezpecnymi vyrazy jsou ekvivalentní $ A_{R} $)
- SQL (silnější, protože má navíc agregační fce, aritmetiku, null...)
💡 Datalog¬ (Stratifikovaný nerekurzivní Datalog¬ je ekvivaletní $ A_{R} $)
| další zdroje |
|---|
|
Věta o tranzitivním uzávěru relace (2×🎓)
| Zážitky ze zkoušek |
|---|
|
Binární relace R je tranzitivní, jestliže ∀abc: (a,b)∈R ∧ (b,c)∈R ⇒ (a,c)∈R.
Tranzitivní uzávěr Rₛ⁺ relace R, je nejmenší tranzitivní relace obsahující R.
- v praxi užitečný – např. hledání spojení s přestupy v dopravě, nebo hledání nejkratší cesty v grafu, apod.
Věta (TC nemůže být vyjádřen v RA ): Pro schéma binární relace R v AR neexistuje výraz, který ∀ relaci R počítá její tranzitivní uzávěr R⁺.
Pozn: 💡 Nestačí ani rozšíření o aritmetické výrazy, agregační fce a ano/ne dotazy, částečné řešení poskytuje Datalog
| Lemma E(Rₛ): |
|---|
|
lze se na to dívat tak, že:
|
Dk (sporem, nechť takové E existuje (je konečné), pak dokážu zvýšit d natolik, že aₘaₘ₊d ∉ E(Rₛ) nebo aₘ₊daₘ ∈ E(Rₛ) a nemělo by být)
- uvažujme binární relaci Rₛ = { aᵢaⱼ | 1 ≤ i < s } ⇒ jejím tranzitivním uzávěrem je Rₛ⁺ = {aᵢaⱼ: i < j}
- ukážeme, že ∄ výraz E(Rₛ) = Rₛ⁺, ∀s
- Lemma: každý RA výraz E můžeme pro dost.velké s vyjádřit jako: E(Rₛ) ≅ { b₁,...,bₖ | Γ(b₁,...,bₖ) }, kde Γ je v DNF
- bᵢ = aⱼ , bᵢ ≠ aⱼ ,
- bᵢ = bⱼ + c nebo bᵢ ≠ bⱼ + c, kde c je (ne nutně kladná) konstanta,
- Dk: indukcí dle počtu operátorů v E
- sporem, nechť takové E existuje, pak můžeme d zvýšit natolik že:
- díky konečnému počtu atomických formulí v Γ: aₘaₘ₊d ∉ E(Rₛ) nebo
- pomocí ≠: aₘ₊daₘ ∈ E(Rₛ) (💡 obojí je spor se definicí TC)
- Tedy: Pro jakýkoliv výraz E vždy existuje s pro něž E(Rₛ) ≠ Rₛ⁺
| Dk (detailně z přednášky s poznámkami - NEvyžaduje se ke zkoušce) |
|---|
|
| další zdroje |
|---|
V češtině u Prof. Pokorného na slajdech. A pokud to někdo náhodou stále nechápe, tak jako já, tak doporučuji materiály z jedné nizozemské univerzity, kde je dopodrobna rozebrán jak důkaz lemmatu, tak hlavního teorému: Lemma1 MainTheorem
|