Formální základy databázové technologie/Datalog

Z ωικι.matfyz.cz
Přejít na: navigace, hledání
Zážitky ze zkoušek  
  • FZDT - Datalog s negací (Pokorný?) - Profesor si přípravu nepřečte pořádně, na škodu studentovi. Očekával jsem, že je hodný, nevyžaduje moc (např. kdybych si vytáhl větu o tr. uzávěru, nechtěl by důkaz), tak jsem se ani neobhajoval; nijak jsem se nechtěl hádat u státnic. Měl jsem popsané asi dvě stránky. Jednou z prvních otázek bylo: "A jak vypadá ten Datalog?" Zas a znovu, jako se stalo jiným, i já jsem spletl termíny term/proměnná/predikát. To, že má člověk praxi v prologu/datalogu, ještě nestačí k tomu, aby správně vysvětlil syntaxi. Dá se říct, že v Datalogu P(x) :- A(x), B(x) je něco jako A(x) & B(x) ⇒ P(x) v logice 1. řádu. Doporučuji psát obecně, ne hned příklady. Profesor si dá záležet na detailech (např. u stratifikace se jednotlivé vrstvy píší jako P1, P2, ..., Pn, tedy čárky místo sjednocení, protože sjednocení by znamenalo, že nám nezáleží na pořadí). Ale kvůli takovým detailům zas nevyhazuje.
  • FZDT - Sémantika Datalogu pomocí NPB (Pokorný) - Posledná otázka, čas už tlačil - Pokorný musel za 45 min. odísť, tak sme sa dali do rozpracovanej otázky. V podstate príjemný rozhovor, na papieri som mal to, čo som si pamätal zo skrípt, akurát mi to veľmi nedávalo dokopy zmysel Skúšajúci bol ale vynikajúci, pýtal sa návodne, prípadne to doplnil. Nič detailné, ani nevyžadoval formalizmy. Ja som zodpovedal čo je to min. pevný bod, ako sa vyhodnocuje, ako sa vyhodnocujú datalog. programy, ako vyzerá EDB, IDB.
  • FZDT - Sémantika Datalogu pomocí NPB (Pokorny) - Takhle by se podle me melo u statnic zkouset. S prihlednutim k tomu, ze je clovek zkousen nejen z ty jedny otazky, ale i ctyrech dalsich. Pritom docela proklepnout, zjistit, co clovek umi, neumi a pustit. Zadnej stres.
  • DMJ - Stratifikovany Datalog s negaci (Pokorny) - Popsal jsem co je stratifikace. Program je stratifikovatelny, kdyz neexistuje v zavislostnim grafu cyklus s negativni hranou. Kdyz je program stratifikovatelny, tak ma MPB (minimalni pevny bod). Vyhodnoceni - pravidla se rozdeli do vrstev a postupne se od prvni vrstvy program vyhodnocuje algoritmem pro Datalog bez negace, tj. naivnim ci semi-naivnim pristupem.


Deduktivní databáze

př. EDB:
F(Oldřich, Pavel)
F(Oldřich, Jaroslav)
F(Jaroslav, Veronika)
př. IDB:
M(x):- F(x,y)
S(y,w) :- F(x,y), F(x,w)
B(x,y) :- S(x,y),M(x)
př. dotazy:
D1: Má Pavel bratra?
D2: Najdi všechny (x,y), kde x je bratrem y
D3: Najdi všechny (x,y), kde x je sourozencem y

je db systém, který dokáže provádět dedukce (např. odvodit další fakta) založené na faktech a pravidlech uložených v (deduktivní) db

Deduktivní db se skládá z:

  • Extenzionální db (EDB) (uložené tabulky) - tvořené fakty
    • fakta - tvrzení, atomické fle obsahující pouze konstanty (statická data, základní informace) - tj. základní literály
      • termy - proměnné nebo konstanty
  • Intenzionální db (IDB) (virtuální relace ≈ "pohledy" z SQL) - množina pravidel: hlava :- tělo
    • pravidla (v IDB) - jsou Hornovy klausule L₀ :- L₁,…,Lₙ (návod jak odvodit data, která nejsou explicitně uložena)
      • literály Lᵢ - jsou atomické formule (nebo negace a.f.) ve tvaru P(t₁,..,tₖ) , kde P je predikátový symbol a tᵢ je proměnná nebo konstanta
      • L₀ hlava pravidla, L₁,…,Lₙ tělo pravidla
      • 💡 tvrzení i literály jsou Hornovy klauzule
    • dotazy - výraz jehož výsledkem jsou nalezená a odvozená data
  • Integritní omezení (IO)
    • tvrzení vymezující korektní DB (na konceptuální a db úrovni)
    • př: název_k jednoznačně identifikuje řádky tabulky Kina
  • jsou výsledkem snahy kombinovat logické programování s relačními db za účelem vytvořit systém, který podporuje mocný formalismus (s vyjadřovacími schopnostmi logických prog. jazyků) a je stále rychlý a schopný pracovat s velmi rozsáhlými objemy dat.
  • mají větší vyjadřovací schopnosti než relační db, ale menší než logické programovací jazyky
další zdroje  


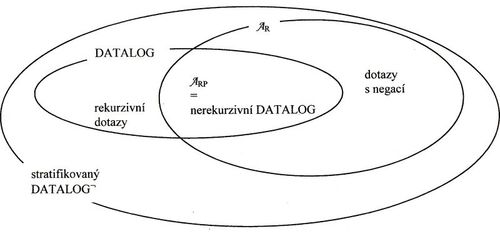
Datalog, 3 sémantiky a jejich ekvivalence.

jazyk používaný v deduktivních db je Datalog - (data)logický program je množinou tvrzení a pravidel

💡 vychází z PROLOGu (Datalog je podmnožinou PROLOGu) a využívá vyhodnocovací algoritmy umožňující efektivnější implementaci (operace relační algebry)
př: nebezpečná pravidla Datalog

z přednášky:

  • GREATER(x,y) :- x > y (není bezpečné)
  • FRIEND(x,y) :- M(x) (není bezpečné)
  • S1(y,w) :- F(x,y), F(x,w), y ≠ w (je bezpečné, ≠ se bere jako =)

z media:Datalog-unsafe_rules.PNG:

  • s(X) :- r(Y) (není bezpečné)
  • s(X) :- r(Y) AND NOT r(X) (není bezpečné)
  • s(X) :- r(Y) AND X < Y (není bezpečné)

(ve všech připadech nekonečnost X splni pravidlo i když je R konečná relace)

Bezpečné pravidla v Datalogu

  • Omezená proměnná x v Datalogu je taková, která se vyskytuje v těle literálu L a pro jehož tělo platí:
    • L je dán pravým predikátem, nebo
      • pravý predikát - jméno zákl.db relace nebo jméno virtuální relace (prakticky EDB nebo levá strana IDB pravidla)
    • L je x = a nebo a = x , kde a je konstanta nebo omezená proměnná

Pravidlo je bezpečné pokud jsou ∀proměnné omezené.

Datalog má povolená pouze bezpečná pravidla a dále platí, že v hlavách jsou pouze jména virtuálních relací

💡 (ktere nejsou v EDB), tzn odvozováním nevytvářím další základní data

Sémantiku logických programů je možné vybudovat minimálně třemi různými způsoby:

logicko-odvozovací přístup (Proof-Theoretic Approach)

  • Metoda: interpretace pravidel jako axiomů použitelných k důkazu, tj. provádíme substituce v těle pravidel a odvozujeme nová tvrzení z hlavy pravidel. V případě DATALOGu tak lze získat právě všechna odvoditelná tvrzení.

logicko-modelový přístup (Model-Theoretic Semantics)

Predstavme si to jako model v logice (analogicke pro logicko-odvozovaci pristup, kde je to take stejne jako v logice - take se z "axiomu" odvozuji vsechna tvrzeni).
  • Metoda: za predikátové symboly dosadíme relace tak, aby na nich byla splněna pravidla.

Příklady z přednášky:

Uvažujme logický program LP 

IDB: P(x) :- Q(x) 
     Q(x) :- R(x)

tj. Q a P označují virtuální relace.

  • Nechť:
R(1) Q(1) P(1) 
Q(2) P(2)         M₁ 
P(3)
Pak relace P*, Q*, R* tvoří model M₁ logického programu LP.
  • Nechť: R(1) (a ostatní tvrzení mají hodnotu FALSE).
Pak relace P*, Q*, R* netvoří model pogického programu LP.
  • Nechť:
R(1) Q(1) P(1) M₂
Pak relace P*, Q*, R* tvoří model M₂ logického programu LP.
  • Nechť EDB: R(1), tj. relační DB je dána jako R* ={(1)}.
Pak M₁ i M₂ jsou s danou databází konzistentní.
  • M₂ tvoří dokonce minimální model, tj. změníme-li v něm cokoliv, porušíme konzistenci.
  • M₁ netvoří minimální model.

💡 při obou sémantikách obdržíme stejný výsledek.

Nevýhody obou přístupů: neefektivní algoritmy v případě, že EDB je dána databázovými relacemi.

příklad MPB: 
%EDB: 
muž(Honza) 
%IDB: 
nudný(x)   :- ¬zábavný(x), muž(x)
zábavný(x) :- ¬nudný(x), muž(x)

pak instance databáze 

I1: {nudný = {Honza}, zábavný = Ø}
I2: {nudný = Ø, zábavný = {Honza}}

jsou dva MPB

(💡 IDB obsahuje neg.cyklus)

pomocí pevného bodu zobrazení (Fixpoint Semantics)

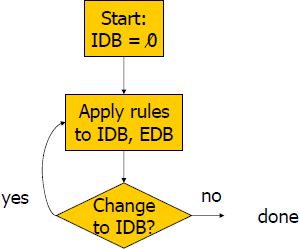
  • Metoda: vyhodnocovací algoritmus + relační db stroj

Nejmenší pevný bod (NPB) rovnice $ R = f(R) $(kde R je bin.schéma relace) je relace $ R^* $ taková, že platí:

  • $ R^* = f(R^*) $ (pevný bod)
  • $ S^* = f(S^*) ⇒R^*⊆ S^* $ (minimalita)

Minimální pevný bod (MPB) pro program je takový pevný bod R*, že neexistuje žádný další pevný bod, který je vlastní podmnožinou R*.

Z toho plyne:

  • ∃ nejmensi pevny bod (NPB), pak je jediným MPB.
  • Existuje-li více MPB, pak jsou navzájem neporovnatelné a NPB neexistuje.
další zdroje  


Datalog s negací, stratifikace.

vyjadřovací síla relačních dotazovacích jazyků
Zážitky ze zkoušek  
  • Datalog s negací (Pokorny) - Profesor si přípravu nepřečte pořádně, na škodu studentovi. Očekával jsem, že je hodný, nevyžaduje moc (např. kdybych si vytáhl větu o tr. uzávěru, nechtěl by důkaz), tak jsem se ani neobhajoval; nijak jsem se nechtěl hádat u státnic. Měl jsem popsané asi dvě stránky. Jednou z prvních otázek bylo: "A jak vypadá ten Datalog?" Zas a znovu, jako se stalo jiným, i já jsem spletl termíny term/proměnná/predikát. To, že má člověk praxi v prologu/datalogu, ještě nestačí k tomu, aby správně vysvětlil syntaxi. Dá se říct, že v Datalogu P(x) :- A(x), B(x) je něco jako $ A(x) \& B(x) \Rightarrow P(x) $ v logice 1. řádu. Doporučuji psát obecně, ne hned příklady. Profesor si dá záležet na detailech (např. u stratifikace se jednotlivé vrstvy píší jako P1, P2, ..., Pn, tedy čárky místo sjednocení, protože sjednocení by znamenalo, že nám nezáleží na pořadí). Ale kvůli takovým detailům zas nevyhazuje.
  • Datalog s negaci (Pokorny) - Co to je ten datalog s negaci, kde se muze negace vyskytovat. (Otazka.. a co kdyby byla negace v hlave pravidla?) Vylozil jsem kde je problem (vic minimalnich modelu), zadefinoval stratifikaci, algoritmus na vypocet datalogickeho programu s negaci, porovnal (bez dk) s Ar.
  • DMJ - Stratifikovany Datalog s negaci (Pokorny) - Popsal jsem co je stratifikace. Program je stratifikovatelny, kdyz neexistuje v zavislostnim grafu cyklus s negativni hranou. Kdyz je program stratifikovatelny, tak ma MPB (minimalni pevny bod). Vyhodnoceni - pravidla se rozdeli do vrstev a postupne se od prvni vrstvy program vyhodnocuje algoritmem pro Datalog bez negace, tj. naivnim ci semi-naivnim pristupem.


$ A_{RP} \{(), [ ], \cup, \times, rename \} $ (pozitivní RA)

Datalog¬

  • Datalog je silnější než $ A_{RP} $, ale existují dotazy v $ A_R $, které v Datalogu nelze vytvořit,
např.:"kteří překladatelé nepřekládají do angličtiny": PŘEKLÁDÁ[JMÉNO] – (KVALIFIKACE(JAZYK=‘ANGL’)[JMÉNO])
  • k vyjádření takovýchto dotazů (obsahujících v relační algebře rozdíl) potřebuje Datalog negaci – je označován Datalog s negací, ovšem způsoby vyhodnocení programů v tomto jazyce obecně nevedou k jednoznačně definovaným virtuálním relacím – proto je identifikována podmnožina Datalogu s negací, která tuto jednoznačnost zajišťuje – tzv. stratifikovaný Datalog (viz dále)

stratifikace

závislostní graf logického programu P: uzly - predikáty z $ R $ a IDB, hrany - $ (U,V) $ je hrana, existuje-li pravidlo $ V :- … U ... $
Graf na obrázku je pro IDB: 
M(x):- F(x,y)
S(y,w) :- F(x,y), F(x,w)
B(x,y) :- S(x,y),M(x)
  • jedná se o rozvrstvení pravidel do vrstev tak, aby byla zajištěna jednoznačnost vyhodnocování programů
  • definujeme pojem definice virtuální relace S, což je množina všech pravidel, kde se S vyskytuje v hlavě
  • Program $ P $ je stratifikovatelný, jestliže existuje disjunktní dělení $ P = P_1 ∪ P_2 .... ∪ P_n $ takové, že plati:
    • vyskytuje-li se predikátový symbol $ S $ pozitivně (je-li obsažen v pozitivním literálu v těle pravidla) v nějakém pravidle $ P_i $, pak je jeho definice obsažena v $ \bigcup_{1 ≤ k ≤ i}P_k $
      • 💡 tj. jeho definice může být ve stejné nebo nižší vrstvě
    • vyskytuje-li se predikátový symbol $ S $ negativně (je-li obsažen v negativním literálu v těle pravidla) v nějakém pravidle $ P_i $, pak je jeho definice obsažena v $ \bigcup_{1 ≤ k < i}P_k $
      • 💡 tj. jeho definice musí být pouze v nižší vrstvě
  • Dělění $ P_1,…, P_n $ se nazývá stratifikace $ P $, každé $ P_i $ je stratum (stratifikace se píše s čárkami pže záleží na pořadí).
  • zjišťování, zda je program stratifikovatelný (a nalezení konkrétního dělení) se provádí pomocí závislostních grafů s ohodnocenými hranami (poz/neg podle výskytu pravidla), jestliže se v grafu vyskytuje cyklus s negativní hranou, není program stratifikovatelný
  • když je program stratifikovatelný ⇒ má MPB

Příklady z přednášky:

  • Program
 P(x) :- ¬ Q(x)       (1)
 R(1)                 (2)
 Q(x) :- Q(x), ¬ R(x) (3)
je stratifikovatelný. Stratifikace:
Stratum 0: (2) R
Stratum 1: (3) Q = Ø
Stratum 2: (1) P = { 1 }
  • Program 
P(x) :- ¬ Q(x)
Q(x) :- ¬ P(x)
není stratifikovatelný.
  • Program pro EDB: METRO(linka, stanice, nasledujici stanice)
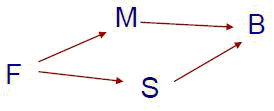
 A(x,x):-METRO(u,x,y)               (1)
 A(x,y):-A(x,z),METRO(u,z,y)        (2)
 B(x,z):-A(x,y),A(z,y),x!=z         (3)
 O1(y):-A(y,Skalka),y!=Krizikova    (4)
 O2(z):-B(z,Krizikova)              (5)
je stratifikovatelný, stratifikace: {(1)} ∪ {(2)} ∪ {(3)} ∪ {(4)} ∪ {(5)}
  • Stratifikovatelný program má obecně více stratifikací. Ty jsou ekvivalentní, tj. vyhodnocení vede ke stejnému MPB
takze at provedu jakoukoliv stratifikaci daneho programu, ziskam MPB, ale nemusi to byt NPB. Viz priklad, kde existuje vice MPB:
%EDB
dil(trojkolka, kolo, 3).
dil(trojkolka, rám, 1).
dil(rám, sedadlo, 1).
dil(rám, pedál, 2).
dil(kolo, ráfek, 1).
dil(kolo, pneumatika, 1).
dil(pneumatika, ventilek, 1).
dil(pneumatika, duse, 1).

%IDB
velky(P) :- dil(P,S,Q), Q > 2.
maly(P) :- dil(P,S,Q), not velky(P).
Stratifikace, a pak výsledný MPB
Stratum 0: Díl
Stratum 1: Velký = {trojkolka}
Stratum 2: Malý = {rám, kolo, pneumatika}
Ale: Relace {Malý = {trojkolka, rám, kolo, duše}, Velký = Ø } tvoří další MPB tohoto programu, ačkoliv není výsledkem stratifikovaného vyhodnocení (💡 v Datalogu není zaručeno pořadí vykonávání operací).

Tvrzení: Nerekurzivní programy DATALOG¬u vyjadřují právě ty dotazy, které jsou vyjádřitelné v $ A_R $.

předpoklad uzavřeného světa
(možná už není ve státnicích)  
* předpoklad uzavřeného světa (CWA) je metapravidlo k odvozování negativní informace
    • jestliže tvrzení R(a1,...,an) není odvoditelné z pravidel (bez použití negace), pak platí not R(a1,...,an) (neboli co není známo, není pravda)
  • předpoklady pro použití CWA
    • různé konstanty neoznačují tentýž objekt
    • doména je uzavřená (konstanty z EDB+IDB) – neexistují relevantní konstanty mimo EDB a IDB
  • Datalog s negací nelze vybudovat na základě CWA
    • program s jediným pravidlem: NUDNÝ(EMIL) :- NOT ZAJÍMAVÝ(EMIL)
    • bylo by odvozeno NOT ZAJÍMAVÝ(EMIL) a NOT NUDNÝ(EMIL), což je ale v rozporu s uvedeným pravidlem – na druhou stranu stratifikace to řeší přirozeně (vezme se prázdná EDB, ZAJÍMAVÝ pak bude mít prázdnou množinu – jelikož nelze odvodit žádný prvek jako ZAJÍMAVÝ a následně se odvozuje NUDNÝ a tam bude {EMIL})
  • příklad z SQL (které používá CWA):
    • SELECT count(*) FROM employees WHERE secondname != „Iljič“
    • spočítej, kolik zaměstnanců má druhé jméno jiné než Iljič – problém nastává u zaměstnanců, kteří mají secondname = NULL, v takovém případě je podmínka ve WHERE vyhodnocena jako UNKNOWN a dle CWA následně jako FALSE, tedy zaměstnanci bez uvedeného druhého jména se do výsledku nezapočtou
další zdroje  
př. rektifikace:

P(a,x,y) :- R(x,y)

P(x,y,x) :- R(y,x)

zavedeme u,v,w , substituce:

P(u,v,w) :- R(x,y), u = a, v = x, w = y

P(u,v,w) :- R(y,x), u = x, v = y, w = x

⇒ P(u,v,w) :- R(v,w), u = a,

P(u,v,w) :- R(v,u), w = u

Algoritmy vyhodnocení dotazů v Datalogu a Datalogu s negací

Obecne pred vyhodnocenim programu se provadi rektifikace - hlavy se stejnym predikatem maji po řadě stejne pojmenovane promenne.

💡 Lemma: rektifikace zachovává bezpečnost a je ekvivaletní původnímu výrazu

Nerekurzivní program

př. algoritmu pro nerekurzivní program:

C(x,y) :- F(x1,x), F(x2,y), S’(x1,x2)

  1. POM(X1,X,X2,Y) = F(X1,X) * F(X2,Y) * S’(X1,X2)
  2. C(X,Y) = POM[X,Y]
  3. S’(Y,W) = (F(X,Y) * F(X,W)) (Y ≠ W)[Y,W]

Jedna se o nerekurzivní program, tedy graf je acyklický. Z toho plyne existence topologického uspořádání. Podle tohoto uspořádání zpracovávám virtuální relace.

  1. pravou stranu převeď na spojení a selekci
  2. proveď na výsledek projekci
  3. předchozí dvě pravidla proveď pro všechna pravidla se stejnou hlavou a výsledek sjednoť

💡 tj. v grafu začnu od uzlu ve kterém končí cesty a znej postupuji zpet k dalsim uzlum a je podle nej vyhodnocuji


Rekurzivní program

Naivní algoritmus
v kazdem kroku algoritmu pracujeme s CELOU vyslednou mnozinou (v kazdem kroku se zbytecne znovu generuji jiz vygenerovane hodnoty). Cyklus konci, kdyz uz nove vysledky nepribyly

Naive-datalog.jpg

zdroj

Polonaivní algoritumus
vylepseni o to, ze se v kazdem kroku pracuje jen s nove vygenerovanou mnozinou
Metoda: 1-krát se použije funkce eval a na diference increval
(analogie s top down dyn.programováním?)

Datalog¬

Mejme priklad: 

zajimavy(X) :- ¬nudny(X), muz(X).
nudny(X) :- ¬zajimavy(X), muz(X).

Extenzionalni tabulka muz obsahuje jeden zaznam 'Honza'. Pak dostavame dva minimalni pevne body (v Datalogu neni zaruceno poradi vykonavani pravidel):

  1. {zajimavy={Honza}, nudny=Ø}
  2. {nudny={Honza}, zajimavy=Ø}

Tento problem neexistence nejmensiho pevneho bodu (i neexistence nejmensiho modelu pro logicko-modelovy přístup + neexistence odvozeni pro logicko-odvozovaci přístup) resi stratifikace (viz definice).

Stratifikovaný DATALOG¬

  • Předpoklady: pravidla jsou bezpečná, rektifikovaná.
  • použije se alg. vyhodnocení Datalogu bez negace, akorát místo případné ¬Q se použije: $ adom^n – Q $
💡 $ adom $ - aktuální doména programu, tj. sjednocení všech konstant z EDB a IDB, $ n $ je počet atributů v Q
další zdroje  
Citováno z „http://wiki.matfyz.cz/index.php?title=Formální_základy_databázové_technologie/Datalog&oldid=35952“