2. Kinematika a dynamika tuhého tělesa
Obsah
Úvod[editovat | editovat zdroj]
Tuhé těleso - nedeformovatelná soustava hmotných bodů, které mají vůči sobě pevné vzdálenosti.
Tuhé těleso má $ 6 $ stupňů volnosti - $ 3 $ rotační a $ 3 $ translační.
Popis rotace:
Zavedeme 2 ortonormální báze: referenční (pevná v prostoru) $ (\vec e_1,\vec e_2,\vec e_3) $ a korotující (pevně spojená s tělesem) $ (\vec e^*_1,\vec e^*_2,\vec e^*_3) $.
Natočení tělesa je pak popsáno ortogonální maticí $ A $:
- $ \vec e^*_i = A_{ik} \vec e_k \, . $
Matice $ A $ je závislá na čase, splňuje relace ortogonality.
Vzpomeňte si na názorný příklad doc. Podolského: kolotoč s koníčkem a slepičkou a opodál stojící Hanka.
Zavedení vektoru úhlové rychlosti[editovat | editovat zdroj]
Uvažujme libovolný časově závislý vektor $ \vec w(t) $,
$ \vec w(t) = w_i(t)\vec e_i = w^*_i(t)\vec e^*_i(t) $,
přičemž $ \vec e^*_i(t) = A_{ik}(t)\vec e_k $.
Pak $ (\frac {d\vec w}{dt})_{prostor} = $
- $ \frac{dw_i}{dt}\vec e_i $ (nahlíženo Hankou)
- $ \frac{dw^*_i}{dt}\vec e^*_i + w^*_i \frac{d\vec e^*_i}{dt} = \frac{dw^*_i}{dt}\vec e^*_i + w_i\frac{dA_{ik}}{dt}A_{jk}\vec e^*_j. $ (nahlíženo slepičkou)
Přeznačíme index i na l a j na i a dostaneme, že
$ \frac{dA_{lk}}{dt}A_{ik} = \Omega^*_{li}. $
Úhlová rychlost $ \Omega $ je antisymetrická (má 3 nezávislé složky a lze s ní asociovat duální pseudovektor).
$ \Omega = \frac{dA}{dt}A^T $
Bez ohledu na zvolenou bázi platí vztah
$ (\frac{d\vec w}{dt})_{prostor(Hanka)} =(\frac{d\vec w}{dt})_{teleso(kolotoc)} + \vec \Omega \times \vec w $
Eulerovy úhly[editovat | editovat zdroj]
Libovolné otočení kolem bodu (těžiště) lze získat 3 po sobě jdoucími otočeními kolem nějaké osy. Zavádíme tzv. Eulerovy úhly. Vezmeme dvě báze: referenční $ \vec x_1,\vec x_2,\vec x_3 $ a korotující $ \vec x^*_1,\vec x^*_2,\vec x^*_3 $. Jejich vzájemná poloha je určena těmito úhly:
- precesní úhel $ \ \phi $ z $ <0,2\pi> $ - nula odpovídá ose $ \vec x_1 $, úhel leží v rovině $ \{\vec x_1,\vec x_2\} $, kladná orientace ve směru osy $ \vec x_2 $; měříme úhel, který svírá osa $ \vec x_1 $ s přímkou $ \vec n $, která vznikne protnutím roviny $ \{\vec x_1,\vec x_2 \} $ a roviny $ \{\vec x^*_1,\vec x^*_2 \} $
- nutační úhel $ \ \theta $ z $ <0,\pi> $ - nula odpovídá ose $ \vec x_3 $, kladná orientace směrem k rovině $ \{\vec x_1,\vec x_2 \} $, měníme úhel mezi osou $ \vec x_3 $ a $ \vec x^*_3 $
- rotační úhel $ \ \psi $ z $ <0,2\pi> $ - nula je v rovině $ \{\vec x_1,\vec x_2\} $, kladná orientace směrem k ose $ \vec x_3 $, měníme úhel mezi přímkou $ \vec n $ a osou $ \vec x^*_1 $.
Jedná se tedy o 3 otočení a vzájemná poloha pevné a korotující báze je pak určena součinem matic těchto otočení.
Eulerovy kinematické rovnice[editovat | editovat zdroj]
Pomocí Eulerových úhlů můžeme vyjádřit vektor úhlové rychlosti, výsledek se nazývá Eulerovy kinetické rovnice.
$ \Omega_x = \dot \phi \sin\theta \sin\psi + \dot \theta \cos\psi \, , $
$ \Omega_y = \dot \phi \sin\theta \cos\psi - \dot \theta \sin\psi \, , $
$ \Omega_z = \dot \phi \cos\theta + \dot \psi \, . $
Tenzor setrvačnosti[editovat | editovat zdroj]
Tenzor setrvačnosti je symetrický tenzor 2. řádu (bilineární funkce nezávisí na pořadí vektorů), lze tedy diagonalizovat. Hlavní osy tenzoru setrvačnosti dostaneme, když budeme v bázi vlastních vektorů.
Přes vektory[editovat | editovat zdroj]
Vyjdeme z celkového momentu hybnosti $ \vec L $ tuhého tělesa
$ \vec L = \sum_{a} \vec r^a \times \vec p^a = \sum_{a} m^a \vec r^a \times \vec v^a $,
kde sčítáme přes všechny hmotné body tuhého tělesa.
$ \vec L = \sum_{a} m^a \vec r^a \times (\vec \Omega \times \vec r^a) $
Zvolme libovolný vektor $ \vec \xi $ a udělejme průmět pomocí skalárního součinu
$ \vec L \cdot \vec \xi = \sum_{a} m^a \vec r^a \times (\vec \Omega \times \vec r^a) \cdot \vec \xi $.
Můžeme udělat cyklickou záměnu a dostaneme
$ \vec L \cdot \vec \xi = \sum_{a} m^a (\vec \xi \times \vec r^a ) \cdot (\vec \Omega \times \vec r^a ) = I (\vec \xi, \vec \Omega) $.
Přes složky[editovat | editovat zdroj]
Uvažujme těleso s rotační energií
$ T_{rot}=\frac{1}{2}\sum_{a} m_a \dot{\vec{r}}_a ^2 = \frac{1}{2}\sum_{a} m_a \left( \vec{\Omega} \times \vec{r}_a \right)^2 $. $ \qquad \left(\star\right) $
Dále užijeme
$ \left( \vec \Omega \times \vec r_a \right)^2 = \vec \Omega^2 (\vec r_a)^2 - \left( \vec \Omega \cdot \vec r_a \right)^2 $ ... platí, protože třeba $ \sin ^2 = 1 - \cos ^2 $.
Rozepíšeme složky vektorů $ \vec \Omega = \Omega_i \vec e_i $ a $ (\vec r_a)_i = (\vec r_a)_i \vec e_i. $
Potom je
$ \left( \vec \Omega \cdot \vec r_a \right)^2 = \Omega_i \Omega_j (r_a)_i (r_a)_j $
a
$ \vec \Omega^2 (\vec r_a)^2 = \Omega_i \Omega_j \vec e_i \vec e_j \cdot (\vec r_a)_i (\vec r_a)_j \vec e_i \vec e_j = \Omega_i \Omega_j \delta_{ij} \cdot \left(\vec r_a \right)^2 $.
Tedy dohromady je
$ \left( \vec \Omega \times \vec r_a \right)^2 = \left[ (\vec r_a)^2 \delta_{ij} - (\vec r_a)_i (\vec r_a)_j \right]\Omega_i \Omega_j $.
Tenzorem setrvačnosti nazvěme člen z $ \left(\star\right) $
$ I_{ij} = \sum_a m_a \left[ (\vec r_a)^2 \delta_{ij} - (\vec r_a)_i (\vec r_a)_j \right] $. $ \qquad\left(\heartsuit\right) $
tak abychom kinetickou energii získali jako
$ T_{rot}=\frac{1}{2} I_{ij}\Omega_i \Omega_j $.
...Tak jest pro diskrétní body.
Pro masiv přepíšeme $ \left(\heartsuit\right) $ do řeči integrálů intuitivně $ I_{ij} = \iiint \mathrm{d} \vec r \rho(\vec r) \left[ (\vec r)^2 \delta_{ij} - r_i r_j \right] $.
Eulerovy dynamické rovnice[editovat | editovat zdroj]
Vyjdeme z 2. věty impulsové (referenční báze):
- $ \left(\frac{d\vec L}{dt}\right)_{\rm Hanka} = \left(\vec M \right)_{\rm Hanka}. $
Pak zvolíme korotující bázi hlavních os tenzoru setrvačnosti
- $ \left(\frac{d\vec L}{dt}\right)_{\rm kolotoc} + \vec \Omega \times \vec L = \vec M $
a dostaneme Eulerovy dynamické rovnice:
- $ I_1 \dot \Omega_x - (I_2 - I_3) \Omega_y \Omega_z = M_x \, , $
- $ I_2 \dot \Omega_y - (I_3 - I_1) \Omega_z \Omega_x = M_y \, , $
- $ I_3 \dot \Omega_z - (I_1 - I_2) \Omega_x \Omega_y = M_z \, . $
Zde jsme použili vztah pro moment hybnosti $ L_i = I_{ij} \Omega_j $ v korotující bázi.
Setrvačníky[editovat | editovat zdroj]
Tuhé těleso, které má pevný bod, nazýváme setrvačníkem. Pokud má těleso navíc osu souměrnosti rozložení hmotnosti (se kterou ztotožňujeme osu $ \vec e^*_3 $), platí navíc $ I_1^{}= I_2 $ a setrvačník je symetrický.
Pokud vyšetřujeme pohyb bezmomentového symetrického setrvačníku, můžeme řešit Eulerovy dynamické rovnice s momenty sil rovnými nule a s podmínkou $ I_1^{} = I_2 $. Dostaneme
$ \psi = \frac{K}{sin\theta_0} t + \psi_0 $
$ \ \theta = \theta_0 $
$ \ \phi = \Omega_0 t + \delta $
Osa souměrnosti setrvačníku se otáčí úhlovou rychlostí $ \dot \psi = \frac{K}{sin\theta_0} $ kolem konstantního směru momentu hybnosti $ \vec L $. Tento kužel pevný v prostoru, jehož osu tvoří vektor momentu hybnosti $ \vec L $ a povrch osa symetrie setrvačníku, nazýváme notačním kuželem. Při pohybu osy souměrnosti setrvačníku po notačním kuželi hovoříme o precesi. Při změně Eulerova úhlu $ \theta $ hovoříme o nutaci.
Na druhou stranu, chceme-li popsat pohyb těžkého symetrického setrvačníku (tj. tuhého tělesa otáčejícího se v tíhovém poli Země), je lepší použít Lagrangeovy rovnice 2. druhu. Lagrangián bude mít tvar ( $ \vec G $ je tíha tělesa, $ \vec r_S $ poloha hmotného středu)
$ \vec L = \frac{1}{2} (I_1 (\Omega_1^2 + \Omega_2^2) + I_3\Omega_3^2) + \vec G \cdot \vec r_S $.
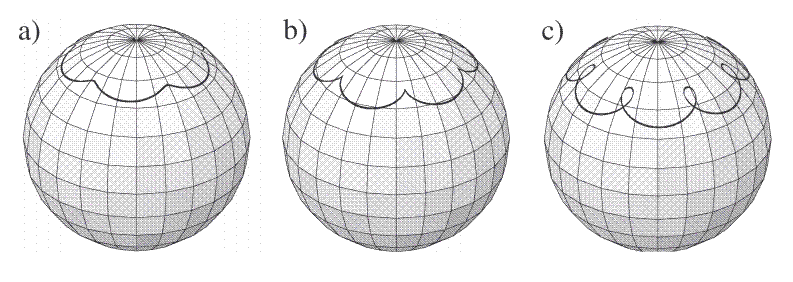
Řešení nelze obecně vyjádřit pomocí elementárních funkcí, jen ve tvaru eliptických integrálů. Lze však provést kvalitativní diskusi. Řešení můžeme dobře znázornit, když kolem bodu upevnění setrvačníků opíšeme kulovou plochu a na ní vyznačíme její průsečík s osou souměrnosti. Průsečík se vždy pohybuje po pásu na kulové ploše. Můžeme rozlišit 3 případy v závislosti na $ \dot \psi $:
- a) $ \dot \psi $ > 0 - průsečík tvoří vlnky,
- b) $ \dot \psi $ = 0 - průsečík tvoří "spojená U" (obrazec mezi vlnkou a smyčkou).
- c) $ \dot \psi $ < 0 - průsečík tvoří smyčky,
Links[editovat | editovat zdroj]
- Poznámky k přednášce doc. Podolského: Tuhé těleso