Automaty a gramatiky
| Automaty a gramatiky | ||||
|
- Bartákova stránka - odkazy, slajdy, cvičení, ...
- Zadání z Modrého - téměř všechno (uz davno neplati), co třeba vědet na zkoušku ...
- [1] - mnoho odkazu a animaci z roku 2008
Obsah
Slovníček pojmů
Kvocient
Levý kvocient
- Levý kvocient L1 podle L2
- L2 \ L1 = { v | uv ∈ L1 & u ∈ L2 }
Levá derivace
- Levá derivace L podle w
- ∂w = {w} \ L
Pravý kvocient
- Pravý kvocient L1 podle L2
- L1 / L2 = { u | uv ∈ L1 & v ∈ L2 }
Pravá derivace
- Pravá derivace L podle w
- ∂Rw = L / {w}
Kongruence
Nechť X je konečná abeceda, $ \sim $ je relace ekvivalence na X*. Potom:
- $ \sim $ je pravá kongruence, jestliže $ \forall u,v,w \in X^* $$ u \sim v \Rightarrow uw \sim vw $
Pokud dvě různá slova u,v převedou automat do stejného stavu (=jsou navzájem ekvivalentní (u ~ v)), pak musí patřit do stejné třídy rozkladu. Pokud k těmto dvěma slovům přidáme stejné slovo zprava, pak tato zřetězená slova budou opět patřit do stejné třídy rozkladu (=musí být navzájem ekvivalentní (uw ~ vw)). A toto je právě ta vlastnost definující pravou kongruenci.
Nerodova věta
Nechť L je jazyk nad konečnou abecedou X. Pak platí:
L je rozpoznatelný konečným automatem $ \Leftrightarrow $ existuje pravá kongruence konečného indexu $ \sim $ na množině X*, pro níž platí, že L je sjednocením jistých tříd rozkladu $ X^*/\sim $ .
Důležité tedy je, že pokud je jazyk regulární, pak pro něj musí existovat pravá kongruence, která (což je nejdůležitější) rozkládá všechna slova jazyka do konečně mnoha tříd.
Iterační (pumping) lemma
Pokud je jazyk L regulární, existuje číslo n > 0 tak, že každé slovo z ∈ L, pro které platí |z| ≥ n, lze zapsat ve tvaru z = uvw, kde pro slova u, v a z platí, že |uv| ≤ n, |v| > 0 a uviw ∈ L pro každé i≥0.
Je to trošku jiná formulace než používá Barták, ale je zní lépe vidět platnost pro konečné jazyky: když je jazyk konečný, tak si za n stačí vzít délku nejdelšího slova a pak to pro všechny slova delší než n (tj. žádná) platí taky.
Kleeneova věta
Jazyk je regulární, právě když je rozpoznatelný konečným automatem.
Důkaz se dá indukcí podle počtu hran v nedeterministickém automatu.
Chomského hierarchie a ti další
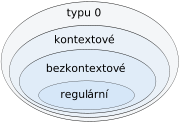
| Zařazení do Chomskeho hierarchie | Gramatiky | Jazyky | Automaty | Pravidla |
|---|---|---|---|---|
| Typu 0 | Gramatiky typu 0 | Rekurzivně spočetné jazyky | Turingův stroj | Pravidla v obecné formě (tj. u → v, kde u,v ∈ (VN∪VT)* a u obsahuje alespoň 1 neternimální symbol) |
| není | (není společný název) | Rekurzivní jazyky | Vždy zastavující Turingův stroj | |
| Typu 1 | Kontextové gramatiky | Kontextové jazyky | Lineárně omezené automaty | Pouze pravidla ve tvaru αXβ → αwβ, X ∈ VN; α,β ∈ (VN∪VT)*; w ∈ (VN∪VT)+
Jedinou výjimkou je pravidlo S → λ, potom se ale S nevyskytuje na pravé straně žádného pravidla. |
| Typu 2 | Bezkontextové gramatiky | Bezkontextové jazyky | (Nedeterministický) Zásobníkový automat | Pouze pravidla ve tvaru X → w, X ∈ VN; w ∈ (VN∪VT)* |
| není | Deterministické bezkontextové gramatiky | Deterministické bezkontextové jazyky | Deterministický zásobníkový automat | |
| Typu 3 | Regulární gramatiky | Regulární (pravé lineární) jazyky | Konečný automat | Pouze pravidla ve tvaru X → wY, X → w; X,Y ∈ VN; w ∈ VT* |
| Každá kategorie jazyků nebo gramatik je podmnožinou jazyků nebo gramatik kategorie přímo nad ní, a jakýkoli automat v každé kategorii má ekvivaletní automat v kategorii přímo nad ním. "není" znamená že nepatří do Chomskeho hierarchie. | ||||
Bezprefixový jazyk
L je bezprefixový, pokud neexistuje slovo u ∈ L takové, že rovněž uw ∈ L, w ∈ X+
Lineární jazyky
Jsou jazyky generované gramatikami s pravidly ve tvaru X->aYb, kde a,b jsou řetězce terminálů a X,Y jsou neterminály. Jsou podmnožinou bezkontextových jazyků, a to vlastní (Dyckův jazyk je bezkontextový, ale není lineární). Viz Lineární gramatiky na wikipedii
(Nedeterministický) Zásobníkový automat
Přijímání koncovým stavem
Skončí když je slovo přečteno a automat je v koncovém stavu.
Přijímání prázdným zásobníkem
Skončí když je slovo přečteno a zásobník je prázdný.
Deterministický zásobníkový automat
Říkáme, že zásobníkový automat M=(Q,X,Y,δ,q0,Z0,F), je deterministický, jestliže platí:
– ∀p∈Q, ∀a∈X∪{λ}, ∀Z∈Y |δ(p,a,Z)|≤1 v kazdem kroku si nemuzeme vybirat
– ∀p∈Q, ∀Z∈Y ( δ(p,λ,Z)≠∅ ⇒ ∀a∈X δ(p,a,Z)=∅ ) definuje ukončení vypoctu
Každý krok výpočtu je přesně určen.