| Zážitky ze zkoušek
|
- R-stromy (2012, Mlýnková) - Napsal jsem, k čemu jsou dobré, definici a štěpení uzlů dle Guttmana a Greeneové. Dále jsem se zmínil o některých variantách R stromů. Zkoušející se pak jen zeptali na pár otázek.
- R-Stromy (2010, Pokorný) - Zadefinovať, k čomu slúžia, nákres, štiepenie Gutmann, Green. Rozhovor pokračoval k MOO, MOK - aproximáciám, aké sú výhody jednotlivých prístupov - náročnosť uloženia vs. schopnosť aproximácie. Žiadne detaily, stačilo rozumieť. R+ stromy som len popísal kritériá výberu osi a distribúcie, vravel som, že to kludne na papier dopíšem, ale Pokorný to zjavne nevyžadoval.
- R-stromy (2009, Skopal) - tuhle otazku jsem tak nejak cekal :-) Bohuzel pan Skopal zkousi pro me dost neprijemnym stylem .. po prvni vete vas dokaze zaskocit nejakou treba i jednoduchou a ne spatne minenou otazkou, na kterou rychle nevite, co odpovedet a pak se do toho tak zamotate, ze zacnete placat nesmysly..on se vas snazi k necemu dokopat, ale kdyz nevite kam presne miri, da se to jen tezko odhadnout..navic z jeho vyrazu nejde vycist, jestli je to jeste v pohode nebo jste na pokraji vyhozeni :-) Nastesti jsem u pana Skopala delal predtim jednu zkousku, tak uz jsem vedel, ze takhle zkousi, ale zas tak zly to neni, jak to v prubehu zkousky vypada...navic me potesilo, ze me nerozebral hned na zacatek uplne a vcas toho nechal..
|
| štěpení uzlu R-Stromu m=3, M=8
|
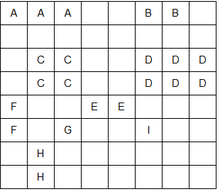
|
|
dle Guttmana:
PickSeeds: největší nevyužitá plocha B,H=44
- ∀PickNext
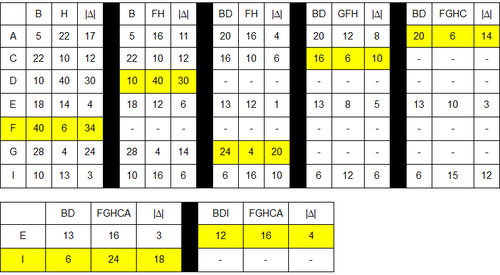
- ⇒ BDIE, FGHCA
|
dle Greene:
- Pick Axis
- PickSeeds: největší nevyužitá plocha B,H=44
- spočteme normované vnitřní vzdálenosti:
- vybereme tu s větší normovanou vzdáleností, tedy y
Distribute: setřídíme objekty podle y souřadnice a rozdělíme
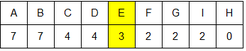
- ⇒ ABCDE, FGIH
|
Typické dotazy na prostorová data jsou:
- vyhledej bod v prostoru
- vyhledej oblast v prostoru
- vyhledej okolí oblasti (bodu)
R-stromy
💡 obdoba B-stromů pro prostorové objekty (ale hledání může jít současně více cestami)
- ∀uzel E má m až M synů (až na kořen - má aspoň 2 syny) a platí: m ≤ M/2
- E.p - identifikátor prostorového objektu (listy) nebo pointer na syna
- E.I - MBR (minimum bounding rectangle) - minimální ohraničující obdélník (MOO)
- 💡 n-dimensionální: MBB (minimum bounding box) - minimální ohraničující kostka (MOK)
- 💡 jednotlivé oblasti se mohou překrývat
- všechny cesty v R-stromu jsou stejně dlouhé (listy na stejné úrovni) ≤ logₘ n
INSERT - štěpení uzlu při jeho M+1 přeplnění (hledám co nejmenší využití prostoru)
Guttman (kvadratická verze, lin.dává horší výsledky)
- PickSeeds - vybrat dvojici prvků s největší nevyužitou plochou
- 💡 napáchaly by největší škodu, pokud bychom je dali do stejné skupiny
- ∀(zbývající uzel) PickNext - postupně k nim přiřazujeme zbylé prvky aby přírustek nev.plochy byl co nejmenší
- |přírustek k původnímu MBR 1.skupiny pomocí dalšího uzlu - přírustek pův. MBR 2.skupiny pomocí stejného uzlu|
- vybereme maximální rozdíl (💡 tj.přidání do op. skupiny by napáchalo největší škodu)
Greenová (snažíme se odstranit překrytí listů - při štěpení vyberem jednu z os)
ChooseAxis (=modifikace Guttmana)
- PickSeeds - z Guttmana
- ∀ osu a MBR(2 prvků) spočti maximální normalizovanou vzdálenost (💡 vnitřní vzdálenost vydělím hranou MBR 2 prvků v dané ose)
- → vyberu osu s největší normalizovanou vzdáleností
- Distribute - větší půlka ⌈(M+1)/2⌉ se hodí do jednoho uzlu a zbytek do druhého uzlu.
- 💡 ne vždy je nalezena vhodná osa – může vést ke špatným výsledkům
R+-stromy
- vnitřní (nelistové) MBR uzly se nepřekrývají ⇒ měně větvení dotazu ALE více dělení a větší výška než R-Stromy
- přiřazuje prostorové objekty do všech listů, do kterých zasahují (tj. odkaz na objekt duplikován)
- u uzlů není zaručena minimální zaplněnost
| štěpení uzlu R*-Stromu m=3, M=8 (jako nahoře)
|

|
ChooseSplitAxis
- seradime podle osy y a počítáme h-okraje
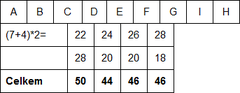
- Celkem: 184
- seradime podle osy x a počítáme h-okraje
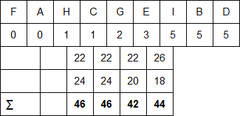
- Celkem: 182
- vybereme tu s menší hodnotou, tedy x
ChooseSplitIndex - počítáme h-překryv když jsou 2 nejmenší stejné tak i h-objem
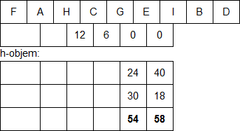
- zase vybereme nejmenší a podle nich rozdělíme
- ⇒ FAHCG, EIBD
|
R*-stromy
- více optimalizačních kritérií oproti R-stromům – minimalizují pokrytí a překrytí pomocí okraje
- rozdíl od R-Stromů: algoritmem na rozdělení přetečené stránky, bere v úvahu více trideni podle os, při přetečení provádí reinsertování, taky algoritmem na hledání listu pro insert (overlap místo nejmenšího rozšíření)
- při INSERTu se v předposlední úrovni vybírá takový list, kde když bude, tak celá ta množina bude mít nejmenší překrytí s ostatními množinami (dalšími listy), ve vyšších úrovních se vybírá uzel, který způsobí nejmenší zvětšení prostoru (jako u R-stromů)
- Split_RS - štěpení
- prvky se setřídí do 2 skupin podle osy x1 a x2
- ∀setřídění jsou vytvořeny všechny kombinace rozdělení prvků tak, aby v 1. skupině bylo aspoň (m-1)+k prvků
- ChooseSplitAxis - ∀osu se dle ní setřídí prvky a spočítá suma margin-value všech distribucí v dané ose a vybere se osa s nejmenší (margin-value sumou)
- ChooseSplitIndex - v této ose se vybere distribuce s nejmenší overlap-value, pokud se rovnají menší area-value
- area-value (h-objem) - součet obou MBR distribucí
- margin-value (h-okraj) - součet okrajů – ve 2D obvod MBR, ve 3D ohraničující plocha MBB distribucí
- overlap-value (h-překrytí) - překrytí obou MBR distribucí
- rozdělíme prvky do 2 distribucí
- Forced Reinsert
- ∀prvky nodu N sestupně setřid podle vzd. od středu MBR
- prvních p prvků odstraň z N a pak je znova insertuj
| další stromy
|
další:
- radix (r^d) stromy
- uvažujme r=2, d=2 rozděluje plochu na 4 čtverce a každý čtverec je reprezentován uzlem stromu, a rekurzivně je dále členěn. Objekt může být uložen v mnoha listech. Strom může být nevyvážený.
- vhodné pouze pokud se celé vejdou do vnitřní paměti
- organizace prostoru – číslování do šířky, adresování cestou, z-uspořádání (peanova křivka), naivní uspořádání, spirálové uspořádání, hilbertova křivka (všechny po sobě jdoucí buňky jsou sousední v prostoru) – volbu organizace je vhodné přizpůsobit datům, pro čtvercové oblasti je vhodné spirálové uspořádání, pro obdélníky je vhodné naivní uspořádání ve směru delší strany
- K-D-stromy
- binární strom – ve vnitřím uzlu je osa podle níž se prostor půlí, v listech jsou B-kostky
- Buddy-stromy
- nepokrývají (nutně) celý prostor
- vhodné pro ukládání bodů (pokud chci složitější struktury je potřeba zdvojnásobit dimenzi a ukládat zvlášť dolní a zvlášť horní mez)
- při slévání se slévají dvě stránky, ale výsledné dělení musí být opět B-dělením (lze k němu dojít pomocí půlení prostoru) – slévat lze kostky, které jsou v poloze „buddy“ – tj. ohraničující kostka sjednocení těchto kostek má s ohraničujícími kostkami ostatních kostek v uzlu prázdný průnik
- prostorové spojení
- motivace: najdi všechny lesy v daném městě – uvažujme jakoby databázi s tabulkou lesů (id_lesu, název_lesu, území) a tabulkou města (id_města, název, území), snahou je vytvořit predikát, který bude fungovat jako spojení v relačních DB – nejčastěji by měl vracet dvojice, které mají neprázdný průnik (ale lze uvažovat i jiné predikáty)
- výsledkem spojení může být buď konkrétní průnik, nebo pouze ukazatele na překrývající se objekty (tzv. Id-spojení)
- prostorové spojení pomocí hnízděných cyklů
- obdoba spojení pomocí setřízení a porovnávání jako u relačních DB není možná prostorové objekty nelze jednoznačně uspořádat do 1 dimenze, jedinou variantou jsou tak hnízděné cykly (porovnají se všechny prvky z tabulky A se všemi z tabulky B) – to je náročné a tak se pokusíme optimalizovat:
- spočítá se spojení MOO těch objektů (kandidáti na správné hity)
- pomocí kvalitnějších aproximací se provede filtrace na jisté hity, jisté chybné hity a nerozhodnuté dvojice
- nerozhodnuté dvojice se rozhodnou pomocí přesné geometrie
- prostorové spojení pomocí z-uspořádání
- vytvoří se mřížka, políčka se očíslují pomocí z-uspořádání (Peanova křivka), objekt je potom aproximován množinou z-hodnot, při porovnávání objektů lze hledat z-hodnotu jednoho objektu mezi z-hodnotami druhého objetku
- prostorové spojení pomocí R-stromů
- nechť jsou prostorové relace uloženy v R-stromech, postupným procházením stromů je možné eliminovat řadu uzlů, protože mají prázdný průnik
- zametací algoritmus
- dvě prostorové relace (uvažujme 2D, obdélník, ev. MOO), každý obdélník je definován svým levým dolním a pravým horním rohem, provedu projekci do jedné osy, najdu obdélník s nejmenší x1 (z obou relací), nechť je to obdélník S1, nyní hledám všechny obdélníky z druhé relace (R), které mají ri.x1 menší než s1.x2. Pokračuji výběrem dalšího obdélníku, ale S1 již neuvažuji (nebude mít průnik s žádným dalším obdélníkem)
|





