Automaty a gramatiky
| Automaty a gramatiky | ||||
|
- Bartákova stránka - odkazy, slajdy, cvičení, ...
- Zadání z Modrého - téměř všechno (uz davno neplati), co třeba vědet na zkoušku ...
- [1] - mnoho odkazu a animaci z roku 2008
Obsah
Slovníček pojmů[editovat | editovat zdroj]
Kvocient[editovat | editovat zdroj]
Levý kvocient[editovat | editovat zdroj]
- Levý kvocient L1 podle L2
- L2 \ L1 = { v | uv ∈ L1 & u ∈ L2 }
Levá derivace[editovat | editovat zdroj]
- Levá derivace L podle w
- ∂w = {w} \ L
Pravý kvocient[editovat | editovat zdroj]
- Pravý kvocient L1 podle L2
- L1 / L2 = { u | uv ∈ L1 & v ∈ L2 }
Pravá derivace[editovat | editovat zdroj]
- Pravá derivace L podle w
- ∂Rw = L / {w}
Kongruence[editovat | editovat zdroj]
Nechť X je konečná abeceda, $ \sim $ je relace ekvivalence na X*. Potom:
- $ \sim $ je pravá kongruence, jestliže $ \forall u,v,w \in X^* $$ u \sim v \Rightarrow uw \sim vw $
Pokud dvě různá slova u,v převedou automat do stejného stavu (=jsou navzájem ekvivalentní (u ~ v)), pak musí patřit do stejné třídy rozkladu. Pokud k těmto dvěma slovům přidáme stejné slovo zprava, pak tato zřetězená slova budou opět patřit do stejné třídy rozkladu (=musí být navzájem ekvivalentní (uw ~ vw)). A toto je právě ta vlastnost definující pravou kongruenci.
Nerodova věta[editovat | editovat zdroj]
Nechť L je jazyk nad konečnou abecedou X. Pak platí:
L je rozpoznatelný konečným automatem $ \Leftrightarrow $ existuje pravá kongruence konečného indexu $ \sim $ na množině X*, pro níž platí, že L je sjednocením jistých tříd rozkladu $ X^*/\sim $ .
Důležité tedy je, že pokud je jazyk regulární, pak pro něj musí existovat pravá kongruence, která (což je nejdůležitější) rozkládá všechna slova jazyka do konečně mnoha tříd.
Iterační (pumping) lemma[editovat | editovat zdroj]
Pokud je jazyk L regulární, existuje číslo n > 0 tak, že každé slovo z ∈ L, pro které platí |z| ≥ n, lze zapsat ve tvaru z = uvw, kde pro slova u, v a z platí, že |uv| ≤ n, |v| > 0 a uviw ∈ L pro každé i≥0.
Je to trošku jiná formulace než používá Barták, ale je zní lépe vidět platnost pro konečné jazyky: když je jazyk konečný, tak si za n stačí vzít délku nejdelšího slova a pak to pro všechny slova delší než n (tj. žádná) platí taky.
Kleeneova věta[editovat | editovat zdroj]
Jazyk je regulární, právě když je rozpoznatelný konečným automatem.
Důkaz se dá indukcí podle počtu hran v nedeterministickém automatu.
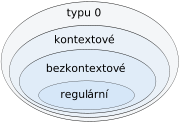
Chomského hierarchie a ti další[editovat | editovat zdroj]
| Zařazení do Chomskeho hierarchie | Gramatiky | Jazyky | Automaty | Pravidla |
|---|---|---|---|---|
| Typu 0 | Gramatiky typu 0 | Rekurzivně spočetné jazyky | Turingův stroj | Pravidla v obecné formě (tj. u → v, kde u,v ∈ (VN∪VT)* a u obsahuje alespoň 1 neternimální symbol) |
| není | (není společný název) | Rekurzivní jazyky | Vždy zastavující Turingův stroj | |
| Typu 1 | Kontextové gramatiky | Kontextové jazyky | Lineárně omezené automaty | Pouze pravidla ve tvaru αXβ → αwβ, X ∈ VN; α,β ∈ (VN∪VT)*; w ∈ (VN∪VT)+
Jedinou výjimkou je pravidlo S → λ, potom se ale S nevyskytuje na pravé straně žádného pravidla. |
| Typu 2 | Bezkontextové gramatiky | Bezkontextové jazyky | (Nedeterministický) Zásobníkový automat | Pouze pravidla ve tvaru X → w, X ∈ VN; w ∈ (VN∪VT)* |
| není | Deterministické bezkontextové gramatiky | Deterministické bezkontextové jazyky | Deterministický zásobníkový automat | |
| Typu 3 | Regulární gramatiky | Regulární (pravé lineární) jazyky | Konečný automat | Pouze pravidla ve tvaru X → wY, X → w; X,Y ∈ VN; w ∈ VT* |
| Každá kategorie jazyků nebo gramatik je podmnožinou jazyků nebo gramatik kategorie přímo nad ní, a jakýkoli automat v každé kategorii má ekvivaletní automat v kategorii přímo nad ním. "není" znamená že nepatří do Chomskeho hierarchie. | ||||
Bezprefixový jazyk[editovat | editovat zdroj]
L je bezprefixový, pokud neexistuje slovo u ∈ L takové, že rovněž uw ∈ L, w ∈ X+
Lineární jazyky[editovat | editovat zdroj]
Jsou jazyky generované gramatikami s pravidly ve tvaru X->aYb, kde a,b jsou řetězce terminálů a X,Y jsou neterminály. Jsou podmnožinou bezkontextových jazyků, a to vlastní (Dyckův jazyk je bezkontextový, ale není lineární). Viz Lineární gramatiky na wikipedii
(Nedeterministický) Zásobníkový automat[editovat | editovat zdroj]
Přijímání koncovým stavem[editovat | editovat zdroj]
Skončí když je slovo přečteno a automat je v koncovém stavu.
Přijímání prázdným zásobníkem[editovat | editovat zdroj]
Skončí když je slovo přečteno a zásobník je prázdný.
Deterministický zásobníkový automat[editovat | editovat zdroj]
Říkáme, že zásobníkový automat M=(Q,X,Y,δ,q0,Z0,F), je deterministický, jestliže platí:
– ∀p∈Q, ∀a∈X∪{λ}, ∀Z∈Y |δ(p,a,Z)|≤1 v kazdem kroku si nemuzeme vybirat
– ∀p∈Q, ∀Z∈Y ( δ(p,λ,Z)≠∅ ⇒ ∀a∈X δ(p,a,Z)=∅ ) definuje ukončení vypoctu
Každý krok výpočtu je přesně určen.