| praktické použití B-stromů:
|
- NTFS adresáře (B+)
- Oracle 11g (B+)
- MS SQL Server 2012 (B+)
- PostgreSQL 9.2 (B+)
- MySQL 5.5 (B+)
|
- Více I2 praktický pohled z OZD - důležitá otázka pro databázisty
- okruhy 14/15: B-stromy a jejich varianty
| Zážitky ze zkoušek
|
- Indexace relacnich dat (2014, Hoksza) - B-stromy a hasovani - -B B+ B* (proc se pouzivaji - velikost vnitrniho uzlu), hashování 7 druhu, viz Hoksza slajdy
- DS - B-stromy a jejich varianty (2014, Kopecký) - Popsal jsem definice, co splňují, operace, vyváženosti a jaké jsou varianty ((ne)redundantní, B+, B*). Pak chtěl pan Kopecký vědět, k čemu jsou dobré (zmínil jsem indexování) a dlouho se ptal na různé detaily (např. jak zabránit zamykání celého B-stromu při insertu pokud se ke stromu přistupuje paralelně - lze provádět dopředný split již naplněného uzlu, jaká varianta stromu je nejlepší pro indexování, které atributy v DB jsou vhodné pro indexování - záleží např. na doméně, atd.)
- DS - B-stromy a jejich varianty (2012) - tady jsem neznal úplně všechny varianty (stacily B/B+/B* jine TEORIE.PDF je neobsahuje), ale nebylo to nijak zásadní, vše hlavní a podstatné jsem věděl, takže OK.
- B-stromy (2012, Dvořák) Napsal sem definici, dukaz logaritmicke vysky ( hrde sem to nazval Veta o logaritmicke vysce Bstromy coz dvorak s usmevem okomentoval ze je to spis takove trivialni pozorovanicko :D ) Pak sem popsal insert a delete. Pak se ptal nato jestli se da insert udelat v jednom pruchodu ( tzn ne ze prvek zatridim a pak vstoupam vzhuru a provadim stepeni preplnenych uzlu...spravna odpoved je delat dopredne stepeni ( kdyz jdu dolu tak plne uzly preventivne rozstepim abych tam mel misto cimz amortizovane zlepsuju slozitost ) Potom A-sort, Redundantni B-stromy, B*-stromy ( tohle vsechno jen v rychlosti...proste chtel vedet ze vim jaka je tam myslenka )
- DS - B-stromy + jejich varianty (2010, nějaký teoretik) - Def., operace, složitosti bez žádných větších důkazů.
- DS - B-stromy a ich varianty (2009, Kopecky) - Napisal som si zakladne definicie B, B+, B* a VB stromov. Pobavili sme sa o redundantych/neredundantych stromoch. Potom o dotazoch na viacero atributov z coho sme sa dostali k hasovaniu a dotazom na ciastocnu zhodu a koncilo to iba otazkou na priestorove data. Tam stacilo povedat, ze je na to dobry R-strom. (Tiez niekde v debate padla otazka na paralelny pristup do B-stromu.) Prijemne aj ked pomerne podrobne sa snazil preverit znalosti.
- I1/I4 DS - B-stromy (2011, Koubek/Majerech) - Zhruba 2 A4, popis (a,b)-stromu, B-strom jako spec. pripad. Odvozeni log. vysky, neformalne zakl. algoritmy, jejich slozitost, varianty B+, B*, preventivni stepeni a slevani, vyuziti: v databazich, index-sekvencni soubory, A-sort. Ptali se me na to definici (dulezity, ze u korene neplati ta podminka na pocet synu) a pak to zacalo: nejdriv rozdil mezi redudantni a neredudantni verzi a jak se tam lisi delete. :( Nejak jsem nedokazal odvodit, kde je to horsi, pak zacal diskutovat Koubek s Majerechem, ze se to takhle neda poradne rict, ze ta slozitost muze byt v nejhorsim pripade stejna (log n, coz jsem rikal), chvilku se "hadali", pak po me chteli amortizovanou slozitost posloupnosti insertu a deletu - odpoved je, ze to vyjde amortizovane O(1) na operaci, ale dokazat jsem to neumel (pry nejak pres potencial, obdobne jako u Fibonaciho haldy). No a jeste se mne docela pacili, proc jsou ty B-stromy pro databaze lepsi, nez streba BVS - no protoze ja to b muzu zvolit tak, ze pak list ~ stranka na disku. Ale pak me nechali uz zit. Asi jsem uplne neoslnil, ale aby me vyhodili, na to to zas nebylo.
|
Tato část je neúplná a potřebuje rozšířit. najít další zkazky a doplnit podle nich
- umožňují při daném klíči najít záznam pomocí několika málo operací, na rozdíl od hashování ale i klíče z nějakého intervalu
- nejčastější pro indexy na externí paměti, pomocí "klastrování" odfiltrujeme nerelevantní záznamy
- setříděný vyvážený m-nární strom s definovanými omezeními větvení (díky nim je rozumně široký)
💡 inserty a delety způsobují pouze lokální změny
pravidla pro neredundatní verzi:
- kořen má ≥2 syny (pokud není list)
- ∀vnitřní uzel (mimo kořene) má od ⌈m/2⌉ do m synů
- ∀uzel má od ⌈m/2⌉-1 do m-1 (poiterů na) datových záznamů
- ∀větev má stejnou délku
- uzly vypadají takhle: p₀,(k₁,p₁,d₁),(k₂,p₂,d₂), ... ,(kₙ,pₙ,dₙ),u (p - pointery, k - klíče - řadí se podle nich, d - data/pointery na data)
- podstromy mají hodnoty klíče mezi klíči z otce
💡 v neredundatních se teoreticky dostaneme rychleji k záznamům (ve vnitřních uzlech)
redundatní - mají datové záznamy pouze v listech, takže klíče jsou redundantní ve vnitřních uzlech
- Implementace
💡 většinou 1 stránka/blok(8kb) = 1 uzel , tedy arita B-Stromu je okolo 500 a výška se drží okolo 3
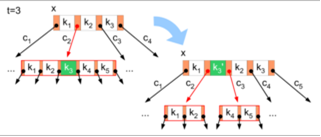
- INSERT
- najdeme list kam vložit a pokud je plný uděláme split takže každý nový list je z půlky plný
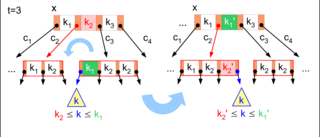
- split můžeme zvýšit počet podstromů otce ⇒ split kaskáda (💡 možná optimalizace: přetékáme do sousedů = vyvažování stránek ⇒ nenastane kaskáda)
- DELETE
- pokud je po delete uzel méně než z pulky plný mergujeme se sousedem
- merge můžeme snížit počet podstromů otce ⇒ merge kaskáda
Oba algoritmy pracují v O(log N) v nejhorším případě.
tedy data (pointry na ně) jsou pouze v listech, a listy jsou propojeny pointery (💡 nelistové vyšší úrovně mouhou být také propojeny - např. MSSQL pro intervalové zámky)
- menší vnitřní uzly ⇒ nižší výška (pže uzly mohou být větší) a tj.rychlejší hledání
- INSERT/DELETE jednodušší ⇒ jednodušší implementace (hlavně range queries)
generalizace vyvažování:
- kořen má ≥2 syny (pokud není list)
- ∀větev má stejnou délku
- ∀uzel má alespoň ⌈(2m-1)/3⌉ synů
- INSERT/DELETE
- Štěpení se odkládá, dokud nejsou sourozenci plní, potom se štěpí buď 2 do 3. Při odebírání se slévají 3 uzly do 2.
💡 detailněji zde: B-Stromy