Obsah

1 Sylabus
2 Volná částice
3 Potenciálová jáma
4 Lineární harmonický oscilátor
5 Vodíku podobný atom

Sylabus

Aplikace kvantové mechaniky Volná částice. Částice v potenciálové jámě. Tunelový jev. Lineární harmonický oscilátor. Atom vodíku.

Státní závěrečná zkouška

Volná částice

- volná -> žádné okrajové podmínky pro vlnovou funkci, nekvantovaná energie a nekvantovaný impuls

Stacionární stavy

- nejdříve vyřešit pro jednu dimensi

Cílem je vyřešit nečasovou Schrödingerovu rovnici (tedy najít tvar $\psi(x)\$ ): $-\frac{h^2}{2m}\frac{d^2\psi (x)}{dx^2} = E\psi (x)\ (17.1)$

Přepíšeme do tvaru $\left(\frac{d^2}{dx^2}+\frac{2mE}{{\hbar}^2}\right)\psi(x)=0\ (17.2)$ a označíme $\frac{2mE}{{\hbar}^2}=k^2\ (17.3)$ , kde $k\$ je vlnový vektor. Když najdeme řešení odpovídajícího charakteristického polynomu ${\lambda}^2+k^2=0\$ , tak odkud dostaneme $\lambda_{1,2}=\pm ik$

Odtud řešení Schrödingerovy rovnice (17.2) $\psi(x)=e^{\pm ikx}\ (17.4)$ .

Z definice operátoru $\hat p=-i\hbar\frac{d}{dx}$ je vidět,že impuls částice s takovou vlnovou funkcí je $p=\pm \hbar k\$ .

Vlnová funkce jde tedy psát ve tvaru $\psi(x)=e^{\frac{-px}{i\hbar}}$ .

Výsledná časová funkce se zapíše jako $\psi(x,t)=e^{\frac{Et-px}{i\hbar}}\ (17.5)$

(impuls $p\$ může nabývat kladných i záporných hodnot) a celková energie částice je její kinetická energie $E=\frac{{\hbar}^2k^2}{2m}=\frac{p^2}{2m}$

Vlnová funkce (17.5) je vlastní funkcí hamiltoniánu $\hat H\psi=\hat T\psi=-\frac{{\hbar}^2}{2m}\frac{d^2\psi}{dx^2}=\frac{p^2}{2m}\psi$ s vlastní energií $E=\frac{p^2}{2m}$ .

Tato funkce je zároveň vlastní funkcí operátoru impulsu $\hat p\psi=-i\hbar\frac{d}{dx}\psi=p\psi$ s vlastní hodnotou $p=\pm \hbar k$ .

Operátory $\hat p\ \mbox{a}\ \hat T$ spolu komutují, $[\hat T, \hat p]=0$ , takže mají stejné vlastní funkce. Jednorozměrný pohyb volné částice jde proto popsat dvěma kvantovými čísly - kinetickou energií $E=\frac{p^2}{2m}$ a impulsem $p\$ .

PS: De Broglieho vztah $p=\pm \hbar k$ nebylo třeba předpokládat, vyšel řešením Schrödingerovy rovnice.

Normování

Vlnová funkce volné částice nelze normovat na jedničku $\|\psi\|^2=1$ . Normuje se proto buď na objem nebo na Diracovu $\delta\$ -funkci.

Na konečný objem

Nejdřív zavedeme umělé kvantování s pomocí cyklické (periodické) hraniční podmínky: $\psi(x)=\psi(x+L)\$ , kde $\psi\$ je vlnová funkce a $L\$ je délka intervalu, po kterém se vlnová funkce periodicky opakuje. To vede na kvantování momentu hybnosti $p_n=\frac{2\pi\hbar n}{L}$ .

Kvůli periodicitě exponenciály stačí uvažovat $n=1..L\$ , kde $L\$ bude velké přirozené číslo. Vzhledem k periodicitě vlnové funkce lze pak zavést normování při integraci přes libovolný interval délky $L\$ , takže dostaneme vlnové funkce s kvantovanými impulsy $\psi(x)_n=\frac{1}{\sqrt{L}}e^{-\frac{p_n x}{i\hbar}}$

Všechny výpočty se pak provádějí s těmito funkcemi, na konci se provede limita $L\to\infty$ . Pro vlnovou funkci závisející na třech prostorových souřadnicích se normování provede pro každou souřadnici zvlášť.

Na $\delta\$ -funkci

Využijeme vyjádření $\delta\$ -fce ve tvaru $\delta(k)=\frac{1}{2\pi\hbar}\int_{R} e^{\frac{-ikx}{\hbar}}dx$ .

Normujeme-li prostorovou část vlnové funkce $\psi(x,t)=e^{\frac{Et-px}{i\hbar}}$ vztahem $\psi(x)_p=\frac{1}{\sqrt{2\pi\hbar}}e^{-\frac{px}{i\hbar}}$ , dostaneme skalární součin $\int_{R}\psi(x)_p^* \psi(x)_{p'} dx = \frac{1}{2\pi\hbar}\int_{R}e^{\frac{x(p-p')}{i\hbar}} dx=\delta(p-p')$ ,

Toto normování má přednost především z hlediska relací úplnosti a Diracovy symboliky.

Obecné řešení časové Schrödingerovy rovnice

Obecné řešení časové Schr. rovnice lze psát jako superposici řešení $\psi(x,t)=\frac{1}{\sqrt{2\pi\hbar}}\int_{R}c(p)e^{\frac{\frac{p^2}{2m}t-px}{i\hbar}}dp$ , kde $c(p)\$ je komplexní koeficient rozvoje do rovinných vln závislý na $p\$ . Funkce $c(p)\$ je Fourierovým obrazem funkce $\psi(x,0)\$ a lze ho určit zpětnou transformací $c(p)=\frac{1}{\sqrt{2\pi\hbar}}\int_{R}\psi(x,0)e^{\frac{px}{i\hbar}}dx.$

Ve 3D tedy $\psi(\mathbf{r},t)=\frac{1}{(2\pi\hbar)^{3/2}}\int_{R}c(\mathbf{p})e^{\frac{\frac{p^2}{2m}t-\mathbf{p}\mathbf{r}}{i\hbar}}d^3\mathbf{p}$ a

$c(\mathbf{p})=\frac{1}{(2\pi\hbar)^{3/2}}\int_{R}\psi(\mathbf{r},0)e^{\frac{\mathbf{p}\mathbf{r}}{i\hbar}}d^3\mathbf{r}.$

Potenciálová jáma

Nekonečně hluboká

1-dimensionální

V intervalu $\langle 0,a \rangle$ položíme potenciál $V(x)=0\$ , mimo tento interval ji položíme nekonečně velkou. Všude kromě intervalu $\langle 0,a \rangle$ bude tedy $\psi(x)=0\$ a pro $\langle 0,a \rangle$ řešíme stacionírní Schrödingerovu rovnici

$\frac{-{\hbar}^2}{2m}\frac{d^2\psi(x)}{dx^2}=E\psi(x)$

To vede na řešení $\psi(x)=Ae^{ikx}+Be^{-ikx}\$ (viz volná částice).

Konstanty $A,\ B$ získáme z podmínek spojitosti $\psi\$ a okrajích, tedy

$\psi(0)=0,\ \psi(a)=0$ .

Vyřešením první podmínky dostaneme $\psi(x)=N\sin(kx)\$ , kde $N=2iA\$ je komplexní konstanta, dosazením do druhé podmínky získáme $\sin(ka)=0\$ , odkud $k=\frac{\pi n}{a}$ .

Jelikož $k^2=\frac{2mE}{{\hbar}^2}$ , jsou tedy energie $E_n=\frac{{\pi}^2{\hbar}^2}{2ma^2}n^2$ a je vidět, že kvantování je důsledkem okrajových podmínek.

Vlnové funkce příslušné těmto energiím jsou $\psi(x)=Nsin(\frac{\pi n}{a}x)$

Konstantu $N\$ určíme z normovacích podmínek $\int_{0}^{a} N^2 {sin^2(\frac{\pi n x}{a})}dx=1,\ \mbox{subst.}\ y=\frac{\pi nx}{a},\ dx=\frac{a dy}{\pi n},\ \frac{aN^2}{\pi n} \int_{0}^{\pi n} {sin^2(y)} dy=1,\ \Rightarrow N=\sqrt{\frac{2}{a}}e^{i\alpha}$

$e^{i\alpha}\$ je fázový faktor ( $N\$ je komplexní číslo, takže $\alpha\$ říká, kam v komplexní rovině to $N\$ míří), obvykla volíme jako $1\$ .

Celkově jsou tedy vlnové funkce $\psi(x)=\sqrt{\frac{2}{a}}sin(\frac{\pi n}{a}x)$

a k nim příslušné energie jsou $E_n=\frac{{\pi}^2{\hbar}^2}{2ma^2}n^2$ .

Energie stacionárních stavů mají tyto vlastnosti:

Energie $E_n\$ jsou větší než nula, stav s energií $E_n\leq 0\$ není možný.

Energetické spektrum $E_n\ , n=1,\ 2,\ 3,\dots$ je diskrétní a nedegenerované.

Energie $E_n\$ jsou úměrné $n^2,\ E_n\sim n^2$ , zatímco jejich rozdíly jsou přibližně lineární v $n\$ $E_n\sim n$ a relarivní rozdíl energií klesá jako $\frac {E_{n+1}-E_n}{E_n}\sim \frac{1}{n}$ . S rostoucím $n\$ se tedy přibližujeme klasickému případu, kdy jsou energie spojité.

Vlnové funkce jsou ortonormální a tvoří bázi Hilbertova prostoru.

Počet uzlů funkcí $\psi_n(x)\$ v intervalu $\langle 0,a \rangle$ je roven $n-1\$ .

Funkce $\psi_n\$ jsou sudé, respektive liché vzhledem ke středu intervalu $\langle 0,a \rangle$ , lze vyjádřit s pomocí jejich parity $(-1)^{n-1}\$ . Vlnová funkce základního stavu $(n=1)\$ je sudá, s rostoucím $n\$ se parita střídavě mění.

Obecné řešení časové Schrödingerovy rovnice je tvaru $\psi(x,t)=\sum_{n=1}^{\infty}c_n\psi_n(x)e^{\frac{E_n t}{i\hbar}}$ .

Koeficienty $c_n\$ jsou určeny počáteční podmínkou pro $t=0\ \psi(x,0)=\sum_{n=1}^{\infty} c_n\psi_n(x)$ , odkud $c_n=\int_{0}^a\psi_n^*(x)\psi(x,0)dx$ .

Z požadavku normování funkce $\int_{R}|\psi(x,t)|^2dx=1\$ plyne

$\int_{0}^a |\psi(x,t)|^2 dx= \sum_{m,n=1}^{\infty} c_m^*c_n \int_{0}^a \psi_m^*(x) \psi_n(x) e^{\frac{(E_n-E_m)t}{i\hbar}}dx=\sum_{n=1}^{\infty} |c_n|^2=1$ .

Pravděpodobnost naměřit energii $E_n\$ ve stavu popsaném vlnovou funkcí $\psi(x,t)\$ je $p_n=|c_n|^2\$ .

3-dimensionální

3D potenciálová jáma je charakterisovaná potenciální energií $V(x,y,z)=0\$ pro $0\leq x\leq a, 0\leq y\leq b, 0\leq z\leq c$ , kde $a,\ b,\ c$ jsou rozměry jámy. Mimo jámu je opět $V\to\infty$ .

Stacionární Schrödingerova rovnice je teď $-\frac{{\hbar}^2}{2m}(\frac{{\partial}^2}{\partial x^2}+\frac{{\partial}^2}{\partial y^2}+\frac{{\partial}^2}{\partial z^2})\psi(x,y,z)=E\psi(x,y,z)$ .

Řešíme separací proměnných $\psi(x,y,z)=\psi_x(x)\psi_y(y)\psi_z(z)\$ , tedy předpokládáme, že $E=E_x+E_y+E_z\$ .

Pro každou vlnovou funkci tak dostaneme stacionární Schr. rovnici

$\frac{-{\hbar}^2}{2m}\frac{d^2\psi_x(x)}{dx^2}=E\psi_x(x),\ \frac{-{\hbar}^2}{2m}\frac{d^2\psi_y(y)}{dy^2}=E\psi_y(y),\ \frac{-{\hbar}^2}{2m}\frac{d^2\psi_z(z)}{dz^2}=E\psi_z(z)$ .

Použitím výsledků z 1D jámy dostaneme (normované) funkce $\psi_{nlm}(x,y,z)=\sqrt{\frac{8}{abc}}sin(\frac{\pi xl}{a})sin(\frac{\pi ym}{b})sin(\frac{\pi zn}{c}),\ l,m,n=1,2,3\dots$ s odpovídajícími energiemi $E_{nlm}=\frac{{\pi}^2{\hbar}^2}{2m}(\frac{l^2}{a^2}+\frac{m^2}{b^2}+\frac{n^2}{c^2})$ .

Je vidět, že např. pro $a=b=c\$ odpovídá některým energiím (vyšším než $E_{111}\$ )několik nezávislých funkcí. Pak jde o degenerovanou energii. Čím vyšší je symetrie hamiltoniánu, tím je vyšší degenerace.

Samozřejmě lze vytvořit i jinou potenciálovou jámu, než pravoúhlou krabici. Potom ale Schr. rovnice obvykle nemá analytické řešení. Řešitelná je např. jáma ve tvaru koule, kde jsou řešením sférické Besselovy funkce.

Konečně hluboká

Předpokládáme, že v jámě (pro $-\frac{a}{2}\leq \frac{a}{2}$ ) je potenciál roven $V=0\$ a mimo jámu je $V=V_0\$ .

Řešíme tedy stacionární Schr. rovnici $(-\frac{{\hbar}^2}{2m} \frac{d^2}{dx^2}+V(x))\psi(x)=E\psi(x)$ .

Tato Schr. rce má spojité energetické spektrum pro $E\geq V_0$ a diskrétní pro $E< V_0\$ .

Hledáme vlnové funkce spojité, jednoznačné, konečné, se spojitými derivacemi v bodech skoku potenciálu.

Diskrétní spektrum

Vzhledem k symetrii se můžeme zabývat řešením pouze pro $x\geq 0$ .

Řešíme tedy rovnice $(\frac{d^2}{dx^2}+k^2)\psi_{II}=0$ , kde $k^2=\frac{2mE}{{\hbar}^2}$ pro $0\geq x \geq \frac{a}{2}$ a $(\frac{d^2}{dx^2}-{\alpha}^2)\psi_{III}=0$ , kde ${\alpha}^2=\frac{2m(V_0-E)}{{\hbar}^2}$ pro $x>\frac{a}{2}$ .

Sudá řešení

Bereme řešení ve tvaru $\psi_{II}=A\cos(kx)\$ a $\psi_{III}=Be^{-\alpha x}\$ , kde $A\$ a $B\$ jsou konstanty.

Ze spojitosti vlnové funkce a její první derivace dostáváme sešívací podmínky:

$A\cos(\frac{ka}{2})=Be^{-\frac{a\alpha}{2}},\ A\sin(\frac{ka}{2})=B\frac{\alpha}{k} e^{-\frac{a\alpha}{2}}$ .

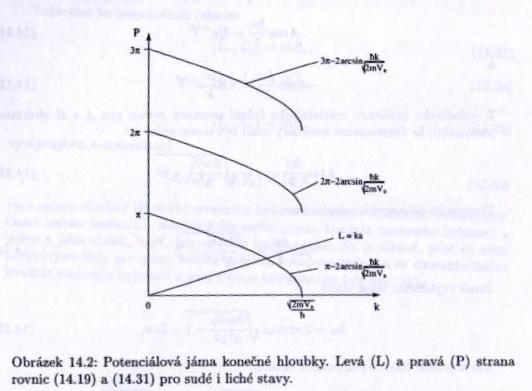
Determinant soustavy musí být 0 (aby existovalo netriviální řešení): $k \operatorname{tg}(\frac{ka}{2})=\alpha=\sqrt{\frac{2mV_0}{{\hbar}^2}-k^2}$ .

Neboli musí platit $ka=2 \operatorname{arctg}(\sqrt{\frac{2mV_0}{{\hbar}^2 k^2}-1})+2\pi n$ , kde $n\$ je celé číslo.

Využitím $\arccos(x)=\operatorname{arctg}(\frac{\sqrt{1-x^2}}{x})=\operatorname{arctg}(\sqrt{\frac{1}{x^2}-1}),\ \arcsin(x)+\arccos(x)=\frac{\pi}{2}$ , dostaneme

$2\operatorname{arctg}(\sqrt{\frac{2mV_0}{{\hbar}^2 k^2}-1}+2\pi n=2\arccos(\frac{\hbar k}{\sqrt{2mV_0}})+2\pi n=-2\arcsin(\frac{\hbar k}{\sqrt{2mV_0}})+(2n+1)\pi.$

Možné hodnoty vlnového vektoru jsou $0 \leq k \leq \frac{\sqrt{2mV_0}}{\hbar}$ a tedy energie $E=\frac{{\hbar}^2 k^2}{2m}$ jsou určeny (pro sudé vázané stavy) vztahem:

$ka=(2n+1)\pi-2\arcsin(\frac{\hbar k}{\sqrt{2mV_0}})$ .

Obrázek ukazuje grafické řešení rovnice. Je vidět, že i pro velmi úzkou a mělkou jámu existuje alespoň jedno řešení, tedy vždy existuje alespoň jeden sudý vázaný stav. S rostoucím a se přímka $L=ka\$ odchyluje od osy $x\$ ; podobně se s rostoucím $V_0\$ posunují křivky pravé strany rovnice doprava. Podle toho se pak objevují další řešení a počet vázaných stavů v diskrétním spektru energií roste. Celkový je sudých vázaných stavů konečně mnoho a aspoň jeden.

Lichá řešení

Analogicky se sudým řešením dostaneme $\psi_{II}=A\sin(kx)\$ a $\psi_{III}=Be^{-\alpha x}\$ ,

sešívací podmínky jsou $A\sin(\frac{ka}{2})=Be^{-\frac{a\alpha}{2}},\ A\cos(\frac{ka}{2})=-B\frac{\alpha}{k} e^{-\frac{a\alpha}{2}}$ ,

nulovost determinantu je určena $k \operatorname{cotg}(\frac{ka}{2})=-\alpha=-\sqrt{\frac{2mV_0}{{\hbar}^2}-k^2}$ .

Podobně tedy řešení pro liché stavy je dáno rovnicí $ka=2n\pi-2\arcsin(\frac{\hbar k}{\sqrt{2mV_0}})$ . Narozdíl od sudých stavů řešení této rovnice nemusí existovat.

Celkově je energií konečně mnoho a existuje aspoň jedna. Vlnové funkce jsou střídavě sudé a liché a jsou nenulové i mimo potenciálovou jámu.

Spojité spektrum

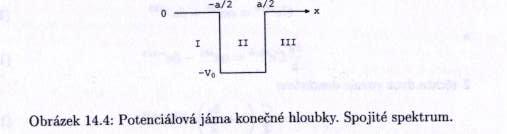
Předpokládáme, že potenciální energie částice s energií $E>0\$ je $V(x)=-V_0\$ pro $-\frac{a}{2}\leq \frac{a}{2}$ a $V(x)=0\$ jinde, přičemž $$ V_0>0 $$ .

Jak se částice pohybuje k jámě, může se od ní buď odrazit nebo oblastí jámy projít.

V oblasti I je vlnová funkce částice $\psi_I=Ae^{ik_0x}+Be^{-ik_0x}\$ , kde

$k_0=\frac{\sqrt{2mE}}{\hbar}\$ , přičemž první část vlnové funkce odpovídá dopadající částici (vlně) a druhá část odpovídá částici (vlně) odrazěné od jámy.

V oblasti II bereme tvar $\psi_{II}=\alpha e^{ikx}+\beta e^{-ikx}\$ , kde $k_0=\frac{\sqrt{2m(E+V_0)}}{\hbar}\$ .

V oblasti III je $\psi_{III}=Ce^{ik_0 x}\$ .

Pravděpodobnost průchodu částice jámou se určí z poměru hustoty toku pravděpodobnosti pro prošlou částici k hustotě toku pravděp. pro dopadající částici. Odtud koeficient odrazu je $R=|\frac{B}{A}|^2\$ a koeficient průchodu je $T=|\frac{C}{A}|^2\$ , přičemž $R+T=1\$ .

Ze sešívacích podmínek v bodě $x=a/2\$ dostaneme

$\alpha=\frac{C}{2}(1+\frac{k_0}{k})e^{i(k_0-k)b}\$ ,

$\beta=\frac{C}{2}(1-\frac{k_0}{k})e^{i(k_0+k)b}\$ .

Ze sešívacích podmínek v $x=-a/2\$ vyjádříme $A\$ a $B\$ , dosadíme $\alpha\$ , $\beta\$ a dostaneme $A,\ B$ vyjádřené pomocí $C\$ .

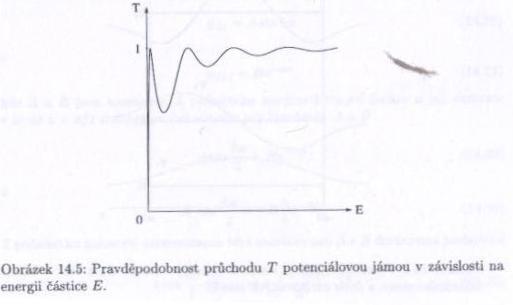
Dosazením do vztahu pro $T\$ dostaneme $T=\frac{1}{1+\frac{1}{4}(\frac{k_0}{k}-\frac{k}{k_0})^2 sin^2(ka)}$ .

Koeficient odrazu je potom $R=1-T\$ .

Pokud potenciálová jáma neexistuje ( $V_0=0\$ ), pak $k=k_0\$ a koeficient průchodu je 1. (Pro hodně mělkou jámu se blíží 1.) $T\$ v závislosti na energii částice $E\$ ukazuje obrázek.

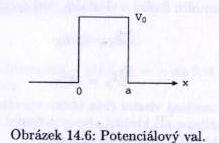
Potenciálový val

Uvažujeme pravoúhlý potenciálový val o šířce $a\$ a výšce $V_0\$ . (taková konečná jáma postavená na hlavu)

Na něj dopadá částice o energii $0<E<V_0\$ , která se s určitou pravděpodobností buď odrazí, nebo projde.

Výsledky pro val dostaneme z výsledků pro jámu záměnou $V_0 \rightarrow -V_0\$ a $k \rightarrow i\kappa\$ .

Vlnový vektor $\kappa\$ je pak $\kappa=\frac{\sqrt{2m(V_0-E)}}{\hbar}>0\$ a je reálný.

Spolu se vztahem $sin(i\kappa a)=i sinh(\kappa a)\$ máme vztah pro koeficient průchodu

$T=\frac{1}{1+\frac{1}{4}(\frac{k_0}{\kappa}+\frac{\kappa}{k_0})^2 sinh^(\kappa a)}$ ,

kde vlnový vektor $k_0=\frac{\sqrt{2mE}}{\hbar}$ odpovídá pohybu volné částice.

Pro libovolně vysoký a široký val existuje určitá pravděpodobnost, že částice projde; s rostoucí šířkou valu a rostoucím rozdílem energií $V_0-E\$ tato pravděpodobnost exponencielně klesá. Pro makroskopické objekty a valy je pravděpodobnost průchodu mizivá.

Lineární harmonický oscilátor

Kvantová mechanika žije v Hilbertově prostoru (HP). Podle toho, jakou zvolíme bázi HP, mluvíme o určité representaci (pokud za bázi zvolímě vlastní vektory operátoru $\hat x$ , mluvíme o x-representaci, pokud vlastní vektory operátoru $\hat p$ , jde o p-representaci atd.). Některé úlohy jde ale řešit i bez konkrétní representace, tedy čistě abstraktně bez volby báze HP.

Hledáme energie LHO bez konkrétní representace, takže chceme najít spektrum (množinu vlastních čísel) operátoru $\hat H$ . Hamiltonián LHO má tvar $\hat H=\frac{{\hat p}^2}{2m}+\frac{1}{2}m{\omega}^2x^2$ .

Zavedeme operátor $\hat K=\frac{1}{2}({\hat P}^2+{\hat X}^2)$ , kde $\hat X$ , $\hat P$ jsou bezrozměrné souřadnice, získané z normálních souřadnic $X=\sqrt{\frac{m\omega}{\hbar}}x, P=\frac{1}{\sqrt{\hbar m\omega}}p$ .

Pro komutátor $x,\ p$ platí $[\hat x, \hat p]=i\hbar$ a komutátor $X,\ P$ je $[\hat X, \hat P]=i$ .

V bezrozměrných souřadnicích a použitím operátoru $\hat K$ má teď hamiltonián tvar $\hat H=\hbar\omega\hat K$ .

Zavedeme kreační a anihilační operátory $\hat a=\frac{1}{\sqrt{2}}(\hat X+i\hat P), \hat a^+ = \frac{1}{\sqrt{2}}(\hat X-i\hat P)$ . S jejich pomocí lze K přepsat jako $\hat K=\hat a^+\hat a +\frac{1}{2}$ .

Využitím $\hat a^+\hat a =\hat K-\frac{1}{2}$ , $[\hat a,\hat a^+]=1$ a $\hat K|n\rangle=k_n|n\rangle$ ( $k_n\$ jsou vlastní čísla operátoru $\hat K$ , $|n\rangle$ jsou jeho vlastní vektory):

$\hat K(\hat a|n\rangle)=(\hat a^+\hat a +\frac{1}{2})\hat a|n\rangle=(\hat a\hat a^+ -\frac{1}{2})\hat a|n\rangle=\hat a\hat a^+\hat a|n\rangle-\frac{1}{2}\hat a|n\rangle=\hat a(\hat K-\frac{1}{2})|n\rangle-\frac{1}{2}\hat a|n\rangle=\hat a(\hat K-1)|n\rangle=(k_n-1)\hat a|n\rangle$

Působením operátoru $\hat a$ tedy dostaneme vyšší stav, působením operátoru $\hat a^+$ stav nižší.

Nelze však snižovat donekonečna, a redy existuje nejnižší stav, který se působením operátoru $\hat a$ již nesníží (respektive dostaneme nulový vektor).

Z vlastností skalárního součinu $\langle n|\hat a^+\hat a|n\rangle=\langle\hat a n|\hat a n\rangle\leq 0$ a tedy $\langle n|\hat K|n\rangle\leq \frac{1}{2}$ .

Tento nejnižší stav je základní, který se značí $|0\rangle$ , tedy $\hat a|n_{min}\rangle=0 = \hat a|0\rangle$ a tedy $\langle 0|\hat K|0\rangle=\frac{1}{2}$

Spektrum operátoru $\hat K$ je $k_n=(n+\frac{1}{2});\ n=1,2,\dots$ a tedy spektrum hamiltoniánu je $E_n=\hbar\omega (n+\frac{1}{2})$ .

Z definičních vztahů pro $\hat a^+,\hat a$ dostaneme tvar $\hat X,\ \hat P$ : $\hat X=\frac{a}{\sqrt{2}}(\hat a +\hat a^+),\ \hat P=\frac{a}{\sqrt{2}}(\hat a -\hat a^+)$ .

V energetické representaci (báze HP jsou vlastní vektory hamiltoniánu) mají matice $\hat a, \hat a^+$ tvar s čísly těsně nad nebo pod diagonálou, matice $\hat H$ je diagonální s vlastními čísly (energiemi) na diagonále.

Harmonický oscilátor se dá samozřejmě řešit i v souřadnicové reprezentaci. Z asymptotického chování vlnové funkce vyplývá, že $\psi(\xi)\sim e^{-\xi^2/2}\$ , kde $\xi=\sqrt{\frac{m\omega}{\hbar}}x$ . Řešení se pak hledá ve tvaru $\psi(\xi)=P(\xi) e^{-\xi^2/2}\$ , kde $P(\xi)\$ je řada ve tvaru $P(\xi)=\sum_{k=0}^{\infty}a_k\xi^k$ . Řěšením Schr. robnice vyjdou vztahy mezi koeficienty $a_k\$ a z požadavku na integrovatelnost vlnové funkce vyjde, že řada musí být konečná a kvantování energií. Vlnové funkce jsou nakonac dány pomocí Hermitových polynomů: $\psi_n=H_n(\xi)e^{-\xi^2/2}\$ , kde $H_n(\xi)=(-1)^ne^{\xi^2}\frac{d^2}{d\xi^n}e^{-\xi^2}$ . Energie vyjdou stejně jako ve Fockově reprezentaci.

Vodíku podobný atom

Při řešení atomu vodíku bychom měli počítat s hamiltoniánem pro elektron a proton. Úloha jde ale rozseparovat na polohu těžiště a relativní vzdálenosti částic. Proton je řádově tisíckrát těžší než elektron, takže počítáme se zafixovaným protonem, okolo kterého obíhá elektron (případně elektron s redukovanou hmotností).

Hamiltonián elektronu v coulombovském poli má tvar:

$\hat H=\frac{{\hat p}^2}{2m}-\frac{Ze'^2}{r}=-\frac{{\hbar}^2}{2m}\Delta-\frac{1}{4\pi\epsilon_0}\frac{Ze^2}{r}$

ve sférických souřadnicích pak $\hat H=-\frac{{\hbar}^2}{2m}[\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r})+\frac{\Delta_{\theta,\phi}}{r^2}]-\frac{1}{4\pi\epsilon_0}\frac{Ze^2}{r}$ . Jelikož hamiltonián komutuje s $\hat L^2$ i $\hat L_z$ , mají všechny tyto operátory společné vlastní funkce.

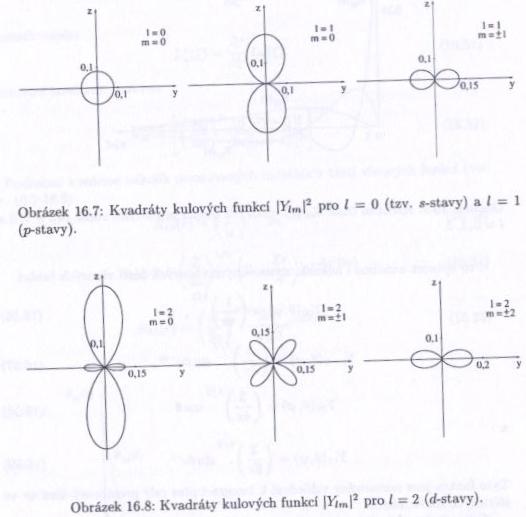
Hledáme vlnové funkce v separovaném tvaru $\psi(r,\theta,\phi)=R(r)Y_{lm}(\theta,\phi)\$ , kde $R(r)\$ je radiální část funkce a kulové funkce $Y_{lm}\$ jsou vlastní funkce operátorů $\hat L^2$ a $\hat L_z$ ,

$\hat L^2Y_{lm}={\hbar}^2l(l+1)Y_{lm},\ l=0,1,2,..$ a $\hat L_z Y_{lm}=\hbar m Y_{lm},\ m=-l,..,l$

Dosazením $\psi\$ v separovaném tvaru do nečasové Schr. rovnice a z předposledního vztahu dostaneme

$\hat H= -\frac{{\hbar}^2}{2m} [\frac{1}{r^2}\frac{d}{dr}(r^2\frac{d}{dr})-\frac {l(l+1)}{r^2}]R-\frac{1}{4\pi\epsilon_0}\frac{Ze^2}{r}R=ER$

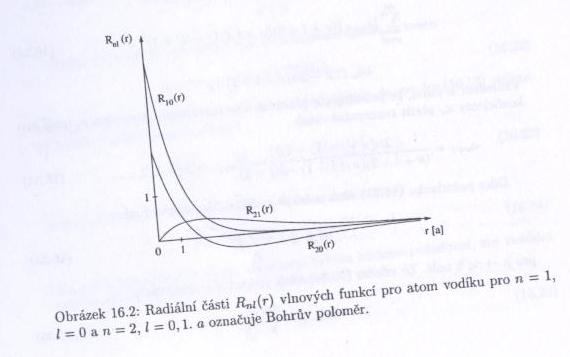
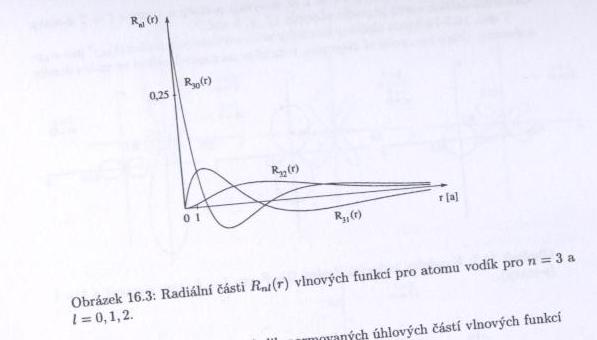
Řešením jsou tzv. Laguerrovy polynomy $R_{nl}(\xi)=N_{nl}e^{-\frac{\xi}{2}}{\xi}^l L^{2l+1}_{n+l}(\xi)$ , kde $\xi=\frac{2Z\rho}{n}=\frac{2Zr}{na}$ .

Normovací koeficient $N_{nl}={\left[\left(\frac{2Z}{na}\right)^3 \frac{(n-l-1)!}{2n[(n+l)!]^3}\right]}^{\frac{1}{2}}$ .

Ve směru $r\$ uplaňujeme okrajovou podmínku $\psi \rightarrow 0$ pro $r\rightarrow \infty$ , čímž získáme kvantování energií $E_n=-\frac{Z^2}{2n^2}\frac{e'^2}{a_0}$ , $n=1,2,\dots$ , kde $a_0=\frac{{\hbar}^2}{me'^2}$ je Bohrův poloměr (vzdálenost, ve které obíhá elektron kolem protonu v základním stavu).

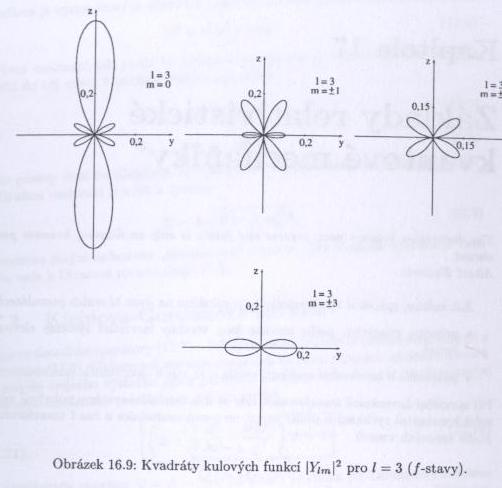
Ke každému $n\$ přísluší stavy s kvantovými čísly $l=0,1,\dots,(n-1)$ (označované písmeny $s,p,d,f,g,\dots$ ) a každý stav s daným $l\$ může navíc nabývat hodnot $m=-l,\dots,l$ . Každý stav je tedy $n^2\$ -krát degenerovaný. Všechny ostatní atomy, ve kterých působí i elektron-elektronová interakce, "náhodnou degeneraci" (nezávislost energie na $l\$ ), která je ve skutečnosti způsobena skrytou symetrií hamiltoniánu, nemají. Elektron v základním stavu atomu vodíku tedy obíhá okolo protonu ve vzdálenosti Bohrova poloměru $a_0\simeq 53 pm$ a má energii $1\$ Rydberg, tedy $13,605 eV\$ . Tvar orbitalu určuje druhá mocnina příslušné kulové funkce.

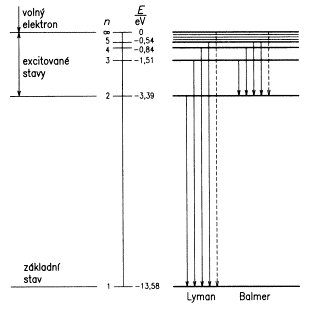
Při přechodech z excitovaných do nižších stavů může vyzářit fotony o energii $E_i-E_f \sim \frac{1}{n_f^2}-\frac{1}{n_i^2}$ . Série přechodu na základní stav $n_f=1\$ je Lymanova, na první excitovaný je Balmerova, na druhý excitovaný Pascheova, na třetí Bracketova a na čvtrý Pfundova. $n_f\$ , $n_i\$ jsou hlavní kvantová čísla.

$E_n=-\frac{\hbar R}{n^2}$ je energie dané elektronové slupky. S rostoucím $n\$ roste i energie, pro $n\rightarrow \infty$ jde $E_n\rightarrow 0$ . V tom případě je energie vazby příliš slabá na to, aby udržela elektron v obalu vodíku; elektron se pak stává volným, jeho energie přestane být kvantovaná a začne být spojitá (může nabýt libovolné hodnoty).

Stav, kdy $n = 1\$ s energií $E_1=-13,6 eV\$ je základní stav vodíku. Energii $13,6 eV\$ musíme atomu dodat, aby se ionizoval. Stavy s vyšší energií se nazývají excitované stavy a pro jejich ionizaci je potřeby nižší energie.