17. Aplikace kvantové mechaniky
Obsah
Sylabus[editovat | editovat zdroj]
Aplikace kvantové mechaniky Volná částice. Částice v potenciálové jámě. Tunelový jev. Lineární harmonický oscilátor. Atom vodíku.
Volná částice[editovat | editovat zdroj]
- volná -> žádné okrajové podmínky pro vlnovou funkci, nekvantovaná energie a nekvantovaný impuls
Stacionární stavy[editovat | editovat zdroj]
- nejdříve vyřešit pro jednu dimensi
Cílem je vyřešit nečasovou Schrödingerovu rovnici (tedy najít tvar $ \psi(x)\ $): $ -\frac{h^2}{2m}\frac{d^2\psi (x)}{dx^2} = E\psi (x)\ (17.1) $
Přepíšeme do tvaru $ \left(\frac{d^2}{dx^2}+\frac{2mE}{{\hbar}^2}\right)\psi(x)=0\ (17.2) $ a označíme $ \frac{2mE}{{\hbar}^2}=k^2\ (17.3) $, kde $ k\ $ je vlnový vektor. Když najdeme řešení odpovídajícího charakteristického polynomu $ {\lambda}^2+k^2=0\ $, tak odkud dostaneme $ \lambda_{1,2}=\pm ik $
Odtud řešení Schrödingerovy rovnice (17.2) $ \psi(x)=e^{\pm ikx}\ (17.4) $.
Z definice operátoru $ \hat p=-i\hbar\frac{d}{dx} $ je vidět,že impuls částice s takovou vlnovou funkcí je $ p=\pm \hbar k\ $.
Vlnová funkce jde tedy psát ve tvaru $ \psi(x)=e^{\frac{-px}{i\hbar}} $.
Výsledná časová funkce se zapíše jako $ \psi(x,t)=e^{\frac{Et-px}{i\hbar}}\ (17.5) $
(impuls $ p\ $ může nabývat kladných i záporných hodnot) a celková energie částice je její kinetická energie $ E=\frac{{\hbar}^2k^2}{2m}=\frac{p^2}{2m} $
Vlnová funkce (17.5) je vlastní funkcí hamiltoniánu $ \hat H\psi=\hat T\psi=-\frac{{\hbar}^2}{2m}\frac{d^2\psi}{dx^2}=\frac{p^2}{2m}\psi $ s vlastní energií
$ E=\frac{p^2}{2m} $.
Tato funkce je zároveň vlastní funkcí operátoru impulsu $ \hat p\psi=-i\hbar\frac{d}{dx}\psi=p\psi $ s vlastní hodnotou $ p=\pm \hbar k $.
Operátory $ \hat p\ \mbox{a}\ \hat T $ spolu komutují, $ [\hat T, \hat p]=0 $, takže mají stejné vlastní funkce. Jednorozměrný pohyb volné částice jde proto popsat dvěma kvantovými čísly - kinetickou energií $ E=\frac{p^2}{2m} $ a impulsem $ p\ $.
PS: De Broglieho vztah $ p=\pm \hbar k $ nebylo třeba předpokládat, vyšel řešením Schrödingerovy rovnice.
Normování[editovat | editovat zdroj]
Vlnová funkce volné částice nelze normovat na jedničku $ \|\psi\|^2=1 $. Normuje se proto buď na objem nebo na Diracovu $ \delta\ $-funkci.
Na konečný objem
Nejdřív zavedeme umělé kvantování s pomocí cyklické (periodické) hraniční podmínky: $ \psi(x)=\psi(x+L)\ $, kde $ \psi\ $ je vlnová funkce a $ L\ $ je délka intervalu, po kterém se vlnová funkce periodicky opakuje. To vede na kvantování momentu hybnosti $ p_n=\frac{2\pi\hbar n}{L} $.
Kvůli periodicitě exponenciály stačí uvažovat $ n=1..L\ $, kde $ L\ $ bude velké přirozené číslo. Vzhledem k periodicitě vlnové funkce lze pak zavést normování při integraci přes libovolný interval délky $ L\ $, takže dostaneme vlnové funkce s kvantovanými impulsy $ \psi(x)_n=\frac{1}{\sqrt{L}}e^{-\frac{p_n x}{i\hbar}} $
Všechny výpočty se pak provádějí s těmito funkcemi, na konci se provede limita $ L\to\infty $. Pro vlnovou funkci závisející na třech prostorových souřadnicích se normování provede pro každou souřadnici zvlášť.
Na $ \delta\ $-funkci
Využijeme vyjádření $ \delta\ $-fce ve tvaru $ \delta(k)=\frac{1}{2\pi\hbar}\int_{R} e^{\frac{-ikx}{\hbar}}dx $.
Normujeme-li prostorovou část vlnové funkce $ \psi(x,t)=e^{\frac{Et-px}{i\hbar}} $ vztahem $ \psi(x)_p=\frac{1}{\sqrt{2\pi\hbar}}e^{-\frac{px}{i\hbar}} $, dostaneme skalární součin $ \int_{R}\psi(x)_p^* \psi(x)_{p'} dx = \frac{1}{2\pi\hbar}\int_{R}e^{\frac{x(p-p')}{i\hbar}} dx=\delta(p-p') $,
Toto normování má přednost především z hlediska relací úplnosti a Diracovy symboliky.
Obecné řešení časové Schrödingerovy rovnice[editovat | editovat zdroj]
Obecné řešení časové Schr. rovnice lze psát jako superposici řešení $ \psi(x,t)=\frac{1}{\sqrt{2\pi\hbar}}\int_{R}c(p)e^{\frac{\frac{p^2}{2m}t-px}{i\hbar}}dp $, kde $ c(p)\ $ je komplexní koeficient rozvoje do rovinných vln závislý na $ p\ $. Funkce $ c(p)\ $ je Fourierovým obrazem funkce $ \psi(x,0)\ $ a lze ho určit zpětnou transformací $ c(p)=\frac{1}{\sqrt{2\pi\hbar}}\int_{R}\psi(x,0)e^{\frac{px}{i\hbar}}dx. $
Ve 3D tedy $ \psi(\mathbf{r},t)=\frac{1}{(2\pi\hbar)^{3/2}}\int_{R}c(\mathbf{p})e^{\frac{\frac{p^2}{2m}t-\mathbf{p}\mathbf{r}}{i\hbar}}d^3\mathbf{p} $ a
$ c(\mathbf{p})=\frac{1}{(2\pi\hbar)^{3/2}}\int_{R}\psi(\mathbf{r},0)e^{\frac{\mathbf{p}\mathbf{r}}{i\hbar}}d^3\mathbf{r}. $
Potenciálová jáma[editovat | editovat zdroj]
Nekonečně hluboká[editovat | editovat zdroj]
1-dimensionální[editovat | editovat zdroj]
V intervalu $ \langle 0,a \rangle $ položíme potenciál $ V(x)=0\ $, mimo tento interval ji položíme nekonečně velkou. Všude kromě intervalu $ \langle 0,a \rangle $ bude tedy $ \psi(x)=0\ $ a pro $ \langle 0,a \rangle $ řešíme stacionírní Schrödingerovu rovnici
$ \frac{-{\hbar}^2}{2m}\frac{d^2\psi(x)}{dx^2}=E\psi(x) $
To vede na řešení $ \psi(x)=Ae^{ikx}+Be^{-ikx}\ $ (viz volná částice).
Konstanty $ A,\ B $ získáme z podmínek spojitosti $ \psi\ $ a okrajích, tedy
$ \psi(0)=0,\ \psi(a)=0 $.
Vyřešením první podmínky dostaneme $ \psi(x)=N\sin(kx)\ $, kde $ N=2iA\ $ je komplexní konstanta, dosazením do druhé podmínky získáme $ \sin(ka)=0\ $, odkud $ k=\frac{\pi n}{a} $.
Jelikož $ k^2=\frac{2mE}{{\hbar}^2} $, jsou tedy energie $ E_n=\frac{{\pi}^2{\hbar}^2}{2ma^2}n^2 $ a je vidět, že kvantování je důsledkem okrajových podmínek.
Vlnové funkce příslušné těmto energiím jsou $ \psi(x)=Nsin(\frac{\pi n}{a}x) $
Konstantu $ N\ $ určíme z normovacích podmínek $ \int_{0}^{a} N^2 {sin^2(\frac{\pi n x}{a})}dx=1,\ \mbox{subst.}\ y=\frac{\pi nx}{a},\ dx=\frac{a dy}{\pi n},\ \frac{aN^2}{\pi n} \int_{0}^{\pi n} {sin^2(y)} dy=1,\ \Rightarrow N=\sqrt{\frac{2}{a}}e^{i\alpha} $
$ e^{i\alpha}\ $ je fázový faktor ($ N\ $ je komplexní číslo, takže $ \alpha\ $ říká, kam v komplexní rovině to $ N\ $ míří), obvykla volíme jako $ 1\ $.
Celkově jsou tedy vlnové funkce $ \psi(x)=\sqrt{\frac{2}{a}}sin(\frac{\pi n}{a}x) $
a k nim příslušné energie jsou $ E_n=\frac{{\pi}^2{\hbar}^2}{2ma^2}n^2 $.
Energie stacionárních stavů mají tyto vlastnosti:
- Energie $ E_n\ $ jsou větší než nula, stav s energií $ E_n\leq 0\ $ není možný.
- Energetické spektrum $ E_n\ , n=1,\ 2,\ 3,\dots $ je diskrétní a nedegenerované.
- Energie $ E_n\ $ jsou úměrné $ n^2,\ E_n\sim n^2 $, zatímco jejich rozdíly jsou přibližně lineární v $ n\ $ $ E_n\sim n $ a relarivní rozdíl energií klesá jako $ \frac {E_{n+1}-E_n}{E_n}\sim \frac{1}{n} $. S rostoucím $ n\ $ se tedy přibližujeme klasickému případu, kdy jsou energie spojité.
- Vlnové funkce jsou ortonormální a tvoří bázi Hilbertova prostoru.
- Počet uzlů funkcí $ \psi_n(x)\ $ v intervalu $ \langle 0,a \rangle $ je roven $ n-1\ $.
- Funkce $ \psi_n\ $ jsou sudé, respektive liché vzhledem ke středu intervalu $ \langle 0,a \rangle $, lze vyjádřit s pomocí jejich parity $ (-1)^{n-1}\ $. Vlnová funkce základního stavu $ (n=1)\ $ je sudá, s rostoucím $ n\ $ se parita střídavě mění.
Obecné řešení časové Schrödingerovy rovnice je tvaru $ \psi(x,t)=\sum_{n=1}^{\infty}c_n\psi_n(x)e^{\frac{E_n t}{i\hbar}} $.
Koeficienty $ c_n\ $ jsou určeny počáteční podmínkou pro $ t=0\ \psi(x,0)=\sum_{n=1}^{\infty} c_n\psi_n(x) $, odkud $ c_n=\int_{0}^a\psi_n^*(x)\psi(x,0)dx $.
Z požadavku normování funkce $ \int_{R}|\psi(x,t)|^2dx=1\ $ plyne
$ \int_{0}^a |\psi(x,t)|^2 dx= \sum_{m,n=1}^{\infty} c_m^*c_n \int_{0}^a \psi_m^*(x) \psi_n(x) e^{\frac{(E_n-E_m)t}{i\hbar}}dx=\sum_{n=1}^{\infty} |c_n|^2=1 $.
Pravděpodobnost naměřit energii $ E_n\ $ ve stavu popsaném vlnovou funkcí $ \psi(x,t)\ $ je $ p_n=|c_n|^2\ $.
3-dimensionální[editovat | editovat zdroj]
3D potenciálová jáma je charakterisovaná potenciální energií $ V(x,y,z)=0\ $ pro $ 0\leq x\leq a, 0\leq y\leq b, 0\leq z\leq c $, kde $ a,\ b,\ c $ jsou rozměry jámy. Mimo jámu je opět $ V\to\infty $.
Stacionární Schrödingerova rovnice je teď $ -\frac{{\hbar}^2}{2m}(\frac{{\partial}^2}{\partial x^2}+\frac{{\partial}^2}{\partial y^2}+\frac{{\partial}^2}{\partial z^2})\psi(x,y,z)=E\psi(x,y,z) $.
Řešíme separací proměnných $ \psi(x,y,z)=\psi_x(x)\psi_y(y)\psi_z(z)\ $, tedy předpokládáme, že $ E=E_x+E_y+E_z\ $.
Pro každou vlnovou funkci tak dostaneme stacionární Schr. rovnici
$ \frac{-{\hbar}^2}{2m}\frac{d^2\psi_x(x)}{dx^2}=E\psi_x(x),\ \frac{-{\hbar}^2}{2m}\frac{d^2\psi_y(y)}{dy^2}=E\psi_y(y),\ \frac{-{\hbar}^2}{2m}\frac{d^2\psi_z(z)}{dz^2}=E\psi_z(z) $.
Použitím výsledků z 1D jámy dostaneme (normované) funkce $ \psi_{nlm}(x,y,z)=\sqrt{\frac{8}{abc}}sin(\frac{\pi xl}{a})sin(\frac{\pi ym}{b})sin(\frac{\pi zn}{c}),\ l,m,n=1,2,3\dots $ s odpovídajícími energiemi $ E_{nlm}=\frac{{\pi}^2{\hbar}^2}{2m}(\frac{l^2}{a^2}+\frac{m^2}{b^2}+\frac{n^2}{c^2}) $.
Je vidět, že např. pro $ a=b=c\ $ odpovídá některým energiím (vyšším než $ E_{111}\ $)několik nezávislých funkcí. Pak jde o degenerovanou energii. Čím vyšší je symetrie hamiltoniánu, tím je vyšší degenerace.
Samozřejmě lze vytvořit i jinou potenciálovou jámu, než pravoúhlou krabici. Potom ale Schr. rovnice obvykle nemá analytické řešení. Řešitelná je např. jáma ve tvaru koule, kde jsou řešením sférické Besselovy funkce.
Konečně hluboká[editovat | editovat zdroj]
Předpokládáme, že v jámě (pro $ -\frac{a}{2}\leq \frac{a}{2} $) je potenciál roven $ V=0\ $ a mimo jámu je $ V=V_0\ $.
Řešíme tedy stacionární Schr. rovnici $ (-\frac{{\hbar}^2}{2m} \frac{d^2}{dx^2}+V(x))\psi(x)=E\psi(x) $.
Tato Schr. rce má spojité energetické spektrum pro $ E\geq V_0 $ a diskrétní pro $ E< V_0\ $.
Hledáme vlnové funkce spojité, jednoznačné, konečné, se spojitými derivacemi v bodech skoku potenciálu.
Diskrétní spektrum[editovat | editovat zdroj]
Vzhledem k symetrii se můžeme zabývat řešením pouze pro $ x\geq 0 $.
Řešíme tedy rovnice $ (\frac{d^2}{dx^2}+k^2)\psi_{II}=0 $, kde $ k^2=\frac{2mE}{{\hbar}^2} $ pro $ 0\geq x \geq \frac{a}{2} $ a $ (\frac{d^2}{dx^2}-{\alpha}^2)\psi_{III}=0 $, kde $ {\alpha}^2=\frac{2m(V_0-E)}{{\hbar}^2} $pro $ x>\frac{a}{2} $.
Sudá řešení
Bereme řešení ve tvaru $ \psi_{II}=A\cos(kx)\ $ a $ \psi_{III}=Be^{-\alpha x}\ $, kde $ A\ $ a $ B\ $ jsou konstanty.
Ze spojitosti vlnové funkce a její první derivace dostáváme sešívací podmínky:
$ A\cos(\frac{ka}{2})=Be^{-\frac{a\alpha}{2}},\ A\sin(\frac{ka}{2})=B\frac{\alpha}{k} e^{-\frac{a\alpha}{2}} $.
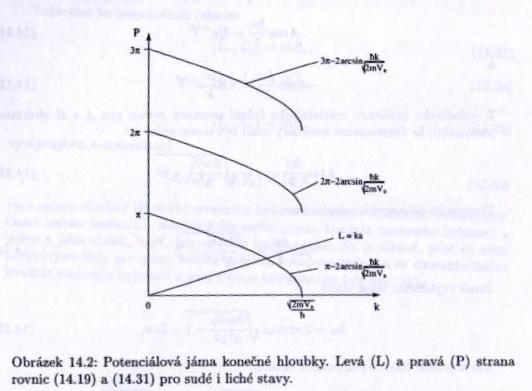
Determinant soustavy musí být 0 (aby existovalo netriviální řešení): $ k \operatorname{tg}(\frac{ka}{2})=\alpha=\sqrt{\frac{2mV_0}{{\hbar}^2}-k^2} $.
Neboli musí platit $ ka=2 \operatorname{arctg}(\sqrt{\frac{2mV_0}{{\hbar}^2 k^2}-1})+2\pi n $, kde $ n\ $ je celé číslo.
Využitím $ \arccos(x)=\operatorname{arctg}(\frac{\sqrt{1-x^2}}{x})=\operatorname{arctg}(\sqrt{\frac{1}{x^2}-1}),\ \arcsin(x)+\arccos(x)=\frac{\pi}{2} $, dostaneme
$ 2\operatorname{arctg}(\sqrt{\frac{2mV_0}{{\hbar}^2 k^2}-1}+2\pi n=2\arccos(\frac{\hbar k}{\sqrt{2mV_0}})+2\pi n=-2\arcsin(\frac{\hbar k}{\sqrt{2mV_0}})+(2n+1)\pi. $
Možné hodnoty vlnového vektoru jsou $ 0 \leq k \leq \frac{\sqrt{2mV_0}}{\hbar} $ a tedy energie $ E=\frac{{\hbar}^2 k^2}{2m} $ jsou určeny (pro sudé vázané stavy) vztahem:
$ ka=(2n+1)\pi-2\arcsin(\frac{\hbar k}{\sqrt{2mV_0}}) $.
Obrázek ukazuje grafické řešení rovnice. Je vidět, že i pro velmi úzkou a mělkou jámu existuje alespoň jedno řešení, tedy vždy existuje alespoň jeden sudý vázaný stav. S rostoucím a se přímka $ L=ka\ $ odchyluje od osy $ x\ $; podobně se s rostoucím $ V_0\ $ posunují křivky pravé strany rovnice doprava. Podle toho se pak objevují další řešení a počet vázaných stavů v diskrétním spektru energií roste. Celkový je sudých vázaných stavů konečně mnoho a aspoň jeden.
Lichá řešení
Analogicky se sudým řešením dostaneme $ \psi_{II}=A\sin(kx)\ $ a $ \psi_{III}=Be^{-\alpha x}\ $,
sešívací podmínky jsou $ A\sin(\frac{ka}{2})=Be^{-\frac{a\alpha}{2}},\ A\cos(\frac{ka}{2})=-B\frac{\alpha}{k} e^{-\frac{a\alpha}{2}} $,
nulovost determinantu je určena $ k \operatorname{cotg}(\frac{ka}{2})=-\alpha=-\sqrt{\frac{2mV_0}{{\hbar}^2}-k^2} $.
Podobně tedy řešení pro liché stavy je dáno rovnicí $ ka=2n\pi-2\arcsin(\frac{\hbar k}{\sqrt{2mV_0}}) $. Narozdíl od sudých stavů řešení této rovnice nemusí existovat.
Celkově je energií konečně mnoho a existuje aspoň jedna. Vlnové funkce jsou střídavě sudé a liché a jsou nenulové i mimo potenciálovou jámu.
Spojité spektrum[editovat | editovat zdroj]
Předpokládáme, že potenciální energie částice s energií $ E>0\ $ je $ V(x)=-V_0\ $ pro $ -\frac{a}{2}\leq \frac{a}{2} $ a $ V(x)=0\ $ jinde, přičemž $ V_0>0 $.
Jak se částice pohybuje k jámě, může se od ní buď odrazit nebo oblastí jámy projít.
V oblasti I je vlnová funkce částice $ \psi_I=Ae^{ik_0x}+Be^{-ik_0x}\ $, kde
$ k_0=\frac{\sqrt{2mE}}{\hbar}\ $, přičemž první část vlnové funkce odpovídá dopadající částici (vlně) a druhá část odpovídá částici (vlně) odrazěné od jámy.
V oblasti II bereme tvar $ \psi_{II}=\alpha e^{ikx}+\beta e^{-ikx}\ $, kde $ k_0=\frac{\sqrt{2m(E+V_0)}}{\hbar}\ $.
V oblasti III je $ \psi_{III}=Ce^{ik_0 x}\ $.
Pravděpodobnost průchodu částice jámou se určí z poměru hustoty toku pravděpodobnosti pro prošlou částici k hustotě toku pravděp. pro dopadající částici. Odtud koeficient odrazu je $ R=|\frac{B}{A}|^2\ $ a koeficient průchodu je $ T=|\frac{C}{A}|^2\ $, přičemž $ R+T=1\ $.
Ze sešívacích podmínek v bodě $ x=a/2\ $ dostaneme
$ \alpha=\frac{C}{2}(1+\frac{k_0}{k})e^{i(k_0-k)b}\ $,
$ \beta=\frac{C}{2}(1-\frac{k_0}{k})e^{i(k_0+k)b}\ $.
Ze sešívacích podmínek v $ x=-a/2\ $ vyjádříme $ A\ $ a $ B\ $, dosadíme $ \alpha\ $, $ \beta\ $ a dostaneme $ A,\ B $ vyjádřené pomocí $ C\ $.
Dosazením do vztahu pro $ T\ $ dostaneme $ T=\frac{1}{1+\frac{1}{4}(\frac{k_0}{k}-\frac{k}{k_0})^2 sin^2(ka)} $.
Koeficient odrazu je potom $ R=1-T\ $.
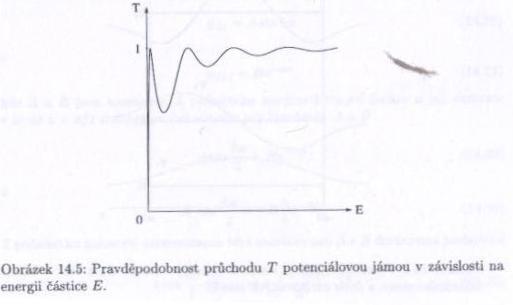
Pokud potenciálová jáma neexistuje ($ V_0=0\ $), pak $ k=k_0\ $ a koeficient průchodu je 1. (Pro hodně mělkou jámu se blíží 1.) $ T\ $ v závislosti na energii částice $ E\ $ ukazuje obrázek.
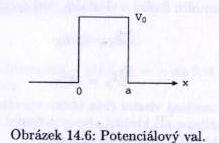
Potenciálový val[editovat | editovat zdroj]
Uvažujeme pravoúhlý potenciálový val o šířce $ a\ $ a výšce $ V_0\ $. (taková konečná jáma postavená na hlavu)
Na něj dopadá částice o energii $ 0<E<V_0\ $, která se s určitou pravděpodobností buď odrazí, nebo projde.
Výsledky pro val dostaneme z výsledků pro jámu záměnou $ V_0 \rightarrow -V_0\ $ a $ k \rightarrow i\kappa\ $.
Vlnový vektor $ \kappa\ $ je pak $ \kappa=\frac{\sqrt{2m(V_0-E)}}{\hbar}>0\ $ a je reálný.
Spolu se vztahem $ sin(i\kappa a)=i sinh(\kappa a)\ $ máme vztah pro koeficient průchodu
$ T=\frac{1}{1+\frac{1}{4}(\frac{k_0}{\kappa}+\frac{\kappa}{k_0})^2 sinh^(\kappa a)} $,
kde vlnový vektor $ k_0=\frac{\sqrt{2mE}}{\hbar} $ odpovídá pohybu volné částice.
Pro libovolně vysoký a široký val existuje určitá pravděpodobnost, že částice projde; s rostoucí šířkou valu a rostoucím rozdílem energií $ V_0-E\ $ tato pravděpodobnost exponencielně klesá. Pro makroskopické objekty a valy je pravděpodobnost průchodu mizivá.
Lineární harmonický oscilátor[editovat | editovat zdroj]
Kvantová mechanika žije v Hilbertově prostoru (HP). Podle toho, jakou zvolíme bázi HP, mluvíme o určité representaci (pokud za bázi zvolímě vlastní vektory operátoru $ \hat x $, mluvíme o x-representaci, pokud vlastní vektory operátoru $ \hat p $, jde o p-representaci atd.). Některé úlohy jde ale řešit i bez konkrétní representace, tedy čistě abstraktně bez volby báze HP.
Hledáme energie LHO bez konkrétní representace, takže chceme najít spektrum (množinu vlastních čísel) operátoru $ \hat H $. Hamiltonián LHO má tvar $ \hat H=\frac{{\hat p}^2}{2m}+\frac{1}{2}m{\omega}^2x^2 $.
Zavedeme operátor $ \hat K=\frac{1}{2}({\hat P}^2+{\hat X}^2) $, kde $ \hat X $, $ \hat P $ jsou bezrozměrné souřadnice, získané z normálních souřadnic $ X=\sqrt{\frac{m\omega}{\hbar}}x, P=\frac{1}{\sqrt{\hbar m\omega}}p $.
Pro komutátor $ x,\ p $ platí $ [\hat x, \hat p]=i\hbar $ a komutátor $ X,\ P $ je $ [\hat X, \hat P]=i $.
V bezrozměrných souřadnicích a použitím operátoru $ \hat K $ má teď hamiltonián tvar $ \hat H=\hbar\omega\hat K $.
Zavedeme kreační a anihilační operátory $ \hat a=\frac{1}{\sqrt{2}}(\hat X+i\hat P), \hat a^+ = \frac{1}{\sqrt{2}}(\hat X-i\hat P) $. S jejich pomocí lze K přepsat jako $ \hat K=\hat a^+\hat a +\frac{1}{2} $.
Využitím $ \hat a^+\hat a =\hat K-\frac{1}{2} $, $ [\hat a,\hat a^+]=1 $ a $ \hat K|n\rangle=k_n|n\rangle $ ($ k_n\ $ jsou vlastní čísla operátoru $ \hat K $, $ |n\rangle $ jsou jeho vlastní vektory):
$ \hat K(\hat a|n\rangle)=(\hat a^+\hat a +\frac{1}{2})\hat a|n\rangle=(\hat a\hat a^+ -\frac{1}{2})\hat a|n\rangle=\hat a\hat a^+\hat a|n\rangle-\frac{1}{2}\hat a|n\rangle=\hat a(\hat K-\frac{1}{2})|n\rangle-\frac{1}{2}\hat a|n\rangle=\hat a(\hat K-1)|n\rangle=(k_n-1)\hat a|n\rangle $
Působením operátoru $ \hat a $ tedy dostaneme vyšší stav, působením operátoru $ \hat a^+ $ stav nižší.
Nelze však snižovat donekonečna, a redy existuje nejnižší stav, který se působením operátoru $ \hat a $ již nesníží (respektive dostaneme nulový vektor).
Z vlastností skalárního součinu $ \langle n|\hat a^+\hat a|n\rangle=\langle\hat a n|\hat a n\rangle\leq 0 $ a tedy $ \langle n|\hat K|n\rangle\leq \frac{1}{2} $.
Tento nejnižší stav je základní, který se značí $ |0\rangle $, tedy $ \hat a|n_{min}\rangle=0 = \hat a|0\rangle $ a tedy $ \langle 0|\hat K|0\rangle=\frac{1}{2} $
Spektrum operátoru $ \hat K $ je $ k_n=(n+\frac{1}{2});\ n=1,2,\dots $ a tedy spektrum hamiltoniánu je $ E_n=\hbar\omega (n+\frac{1}{2}) $.
Z definičních vztahů pro $ \hat a^+,\hat a $ dostaneme tvar $ \hat X,\ \hat P $: $ \hat X=\frac{a}{\sqrt{2}}(\hat a +\hat a^+),\ \hat P=\frac{a}{\sqrt{2}}(\hat a -\hat a^+) $.
V energetické representaci (báze HP jsou vlastní vektory hamiltoniánu) mají matice $ \hat a, \hat a^+ $ tvar s čísly těsně nad nebo pod diagonálou, matice $ \hat H $ je diagonální s vlastními čísly (energiemi) na diagonále.
Harmonický oscilátor se dá samozřejmě řešit i v souřadnicové reprezentaci. Z asymptotického chování vlnové funkce vyplývá, že $ \psi(\xi)\sim e^{-\xi^2/2}\ $, kde $ \xi=\sqrt{\frac{m\omega}{\hbar}}x $. Řešení se pak hledá ve tvaru $ \psi(\xi)=P(\xi) e^{-\xi^2/2}\ $, kde $ P(\xi)\ $ je řada ve tvaru $ P(\xi)=\sum_{k=0}^{\infty}a_k\xi^k $. Řěšením Schr. robnice vyjdou vztahy mezi koeficienty $ a_k\ $ a z požadavku na integrovatelnost vlnové funkce vyjde, že řada musí být konečná a kvantování energií. Vlnové funkce jsou nakonac dány pomocí Hermitových polynomů: $ \psi_n=H_n(\xi)e^{-\xi^2/2}\ $, kde $ H_n(\xi)=(-1)^ne^{\xi^2}\frac{d^2}{d\xi^n}e^{-\xi^2} $. Energie vyjdou stejně jako ve Fockově reprezentaci.
Vodíku podobný atom[editovat | editovat zdroj]
Při řešení atomu vodíku bychom měli počítat s hamiltoniánem pro elektron a proton. Úloha jde ale rozseparovat na polohu těžiště a relativní vzdálenosti částic. Proton je řádově tisíckrát těžší než elektron, takže počítáme se zafixovaným protonem, okolo kterého obíhá elektron (případně elektron s redukovanou hmotností).
Hamiltonián elektronu v coulombovském poli má tvar:
$ \hat H=\frac{{\hat p}^2}{2m}-\frac{Ze'^2}{r}=-\frac{{\hbar}^2}{2m}\Delta-\frac{1}{4\pi\epsilon_0}\frac{Ze^2}{r} $
ve sférických souřadnicích pak $ \hat H=-\frac{{\hbar}^2}{2m}[\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial}{\partial r})+\frac{\Delta_{\theta,\phi}}{r^2}]-\frac{1}{4\pi\epsilon_0}\frac{Ze^2}{r} $. Jelikož hamiltonián komutuje s $ \hat L^2 $ i $ \hat L_z $, mají všechny tyto operátory společné vlastní funkce.
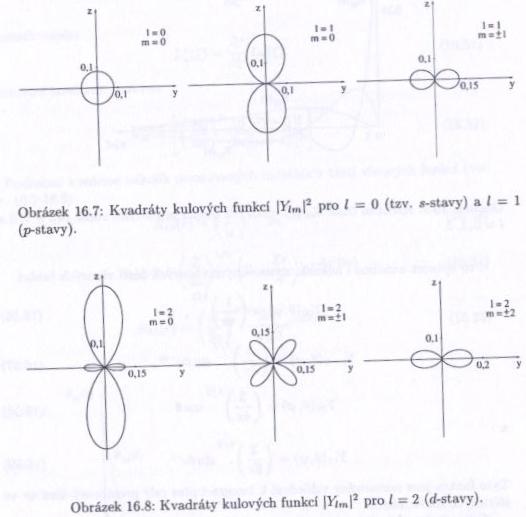
Hledáme vlnové funkce v separovaném tvaru $ \psi(r,\theta,\phi)=R(r)Y_{lm}(\theta,\phi)\ $, kde $ R(r)\ $ je radiální část funkce a kulové funkce $ Y_{lm}\ $ jsou vlastní funkce operátorů $ \hat L^2 $ a $ \hat L_z $,
$ \hat L^2Y_{lm}={\hbar}^2l(l+1)Y_{lm},\ l=0,1,2,.. $ a $ \hat L_z Y_{lm}=\hbar m Y_{lm},\ m=-l,..,l $
Dosazením $ \psi\ $ v separovaném tvaru do nečasové Schr. rovnice a z předposledního vztahu dostaneme
$ \hat H= -\frac{{\hbar}^2}{2m} [\frac{1}{r^2}\frac{d}{dr}(r^2\frac{d}{dr})-\frac {l(l+1)}{r^2}]R-\frac{1}{4\pi\epsilon_0}\frac{Ze^2}{r}R=ER $
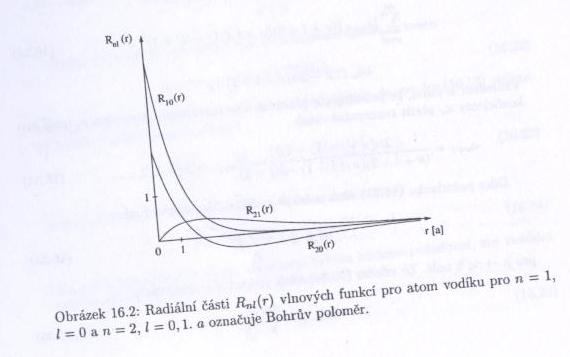
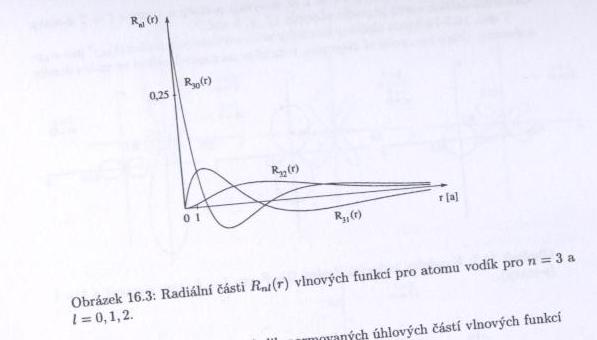
Řešením jsou tzv. Laguerrovy polynomy $ R_{nl}(\xi)=N_{nl}e^{-\frac{\xi}{2}}{\xi}^l L^{2l+1}_{n+l}(\xi) $, kde $ \xi=\frac{2Z\rho}{n}=\frac{2Zr}{na} $.
Normovací koeficient $ N_{nl}={\left[\left(\frac{2Z}{na}\right)^3 \frac{(n-l-1)!}{2n[(n+l)!]^3}\right]}^{\frac{1}{2}} $.
Ve směru $ r\ $ uplaňujeme okrajovou podmínku $ \psi \rightarrow 0 $ pro $ r\rightarrow \infty $, čímž získáme kvantování energií $ E_n=-\frac{Z^2}{2n^2}\frac{e'^2}{a_0} $, $ n=1,2,\dots $, kde $ a_0=\frac{{\hbar}^2}{me'^2} $ je Bohrův poloměr (vzdálenost, ve které obíhá elektron kolem protonu v základním stavu).
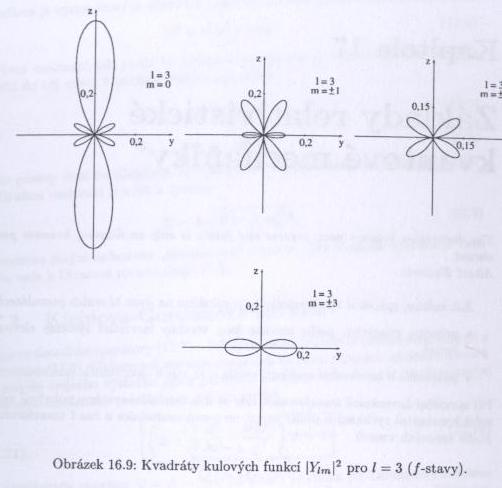
Ke každému $ n\ $ přísluší stavy s kvantovými čísly $ l=0,1,\dots,(n-1) $ (označované písmeny $ s,p,d,f,g,\dots $) a každý stav s daným $ l\ $ může navíc nabývat hodnot $ m=-l,\dots,l $. Každý stav je tedy $ n^2\ $-krát degenerovaný. Všechny ostatní atomy, ve kterých působí i elektron-elektronová interakce, "náhodnou degeneraci" (nezávislost energie na $ l\ $), která je ve skutečnosti způsobena skrytou symetrií hamiltoniánu, nemají. Elektron v základním stavu atomu vodíku tedy obíhá okolo protonu ve vzdálenosti Bohrova poloměru $ a_0\simeq 53 pm $ a má energii $ 1\ $ Rydberg, tedy $ 13,605 eV\ $. Tvar orbitalu určuje druhá mocnina příslušné kulové funkce.
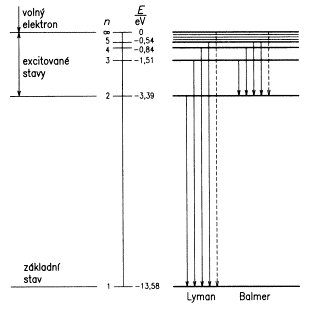
Při přechodech z excitovaných do nižších stavů může vyzářit fotony o energii $ E_i-E_f \sim \frac{1}{n_f^2}-\frac{1}{n_i^2} $. Série přechodu na základní stav $ n_f=1\ $ je Lymanova, na první excitovaný je Balmerova, na druhý excitovaný Pascheova, na třetí Bracketova a na čvtrý Pfundova. $ n_f\ $, $ n_i\ $ jsou hlavní kvantová čísla.
$ E_n=-\frac{\hbar R}{n^2} $ je energie dané elektronové slupky. S rostoucím $ n\ $ roste i energie, pro $ n\rightarrow \infty $ jde $ E_n\rightarrow 0 $. V tom případě je energie vazby příliš slabá na to, aby udržela elektron v obalu vodíku; elektron se pak stává volným, jeho energie přestane být kvantovaná a začne být spojitá (může nabýt libovolné hodnoty).
Stav, kdy $ n = 1\ $ s energií $ E_1=-13,6 eV\ $ je základní stav vodíku. Energii $ 13,6 eV\ $ musíme atomu dodat, aby se ionizoval. Stavy s vyšší energií se nazývají excitované stavy a pro jejich ionizaci je potřeby nižší energie.