Adaptivní agenti a evolucní algoritmy
Obsah
- 1 Rozsah látky
- 2 Materiály
- 3 Architektura autonomního agenta
- 4 Metody pro řízení agentů, řídící architektury
- 4.1 Řídící architektury podle Wooldridge
- 4.2 Symbolické a konekcionistické reaktivní plánování
- 4.3 Srovnání s plánovacími technikami
- 5 Problém hledání cesty; navigační pravidla, reprezentace terénu
- 6 Komunikace a znalosti v multiagentních systémech, ontologie, problém omezené racionality, Kripkeho sémantika možných světu.
- 7 Etologické motivace, modely populační dynamiky.
- 8 Metody pro učení agentů; zpětnovazební učení, základní formy učení zvířat
- 9 Umělá evoluce; genetické algoritmy
- 10 Reprezentační schémata, hypotéza o stavebních blocích.
- 11 Genetické a evoluční programování
- 12 Pravděpodobnostní modely jednoduchého genetického algoritmu.
- 13 Koevoluce, otevrená evoluce.
- 14 Aplikace evolučních algoritmů
Rozsah látky[editovat | editovat zdroj]
Oficiální seznam otázek ([1] léto 2011):
- Architektura autonomního agenta; percepce, mechanismus výběru akcí, paměť; psychologické inspirace. Metody pro řízení agentů; řídící architektury podle Wooldridge, symbolické a konekcionistické reaktivní plánování, hybridní přístupy (Belief Desire Intention, Soar), srovnání s plánovacími technikami. Problém hledání cesty; navigační pravidla, reprezentace terénu. Komunikace a znalosti v multiagentních systémech, ontologie, problém omezené racionality, Kripkeho sémantika možných světů. Etologické motivace, modely populační dynamiky. Metody pro učení agentů; zpětnovazební učení, základní formy učení zvířat.
- Umělá evoluce; genetické algoritmy, genetické a evoluční programování. Základní přístupy a pojmy: populace, fitness, rekombinace, genetické operátory; dynamická vs. statická selekce, mechanismus rulety, turnaje, elitismus. Reprezentační schémata, hypotéza o stavebních blocích. Pravděpodobnostní modely jednoduchého genetického algoritmu. Koevoluce, otevřená evoluce. Aplikace evolučních algoritmů (výběr akcí, evoluce expertních systému, konečných automatu, adaptace evolučních pravidel, neuroevoluce, řešení kombinatorických úloh).
Materiály[editovat | editovat zdroj]
Materiály pro učení v současné době (2011) představují trochu problém. Slajdy z předmětu Umělé bytosti představují osnovu učiva, pro kvalitní naučení však nejsou dostatečné. :( Níže je uveden seznam možných zdrojů - slajdy z přednášek, doporučená literatura, ostatní.
Slajdy
- slajdy z předmětu Umělé bytosti - odkaz
- slajdy na Evoluční algoritmy 1 a 2 od Romana Nerudy
- vybrané kapitoly z přednášek Umělá inteligence 1 a 2 - agenti, úvod do plánování, zpětnovazební účení
- slajdy na Znalosti v multiagentových systémech - první dvě lekce (k nalezení na http://ktiml.mff.cuni.cz/index.php?select=teaching§ion=sources&lang=czech)
Knihy
Níže uvedený seznam je převzat z oficiální stránky obsahující seznam literatury, ze které se lze naučit na státnicový okruh Adaptivní agenti a evoluční algoritmy [2]. Zvýrazněny jsou knihy skutečně dostupné v naší knihovně (z kterých jsem osobně čerpal při učení).
- Michael Wooldridge: An Introduction to MultiAgent Systems. Willey (2002) 1st ed. (nebo 2nd ed. v rozsahu 1st ed.) - Pozn.: silně doporučuji, velice dobrý zdroj!!!
- Gerhard Weiss (editor): Multiagent Systems: A Modern Approach to Distributed Artificial Intelligence. - Pozn.: velmi dobrý úvod
- Richard S. Sutton and Andrew G. Barto: Reinforcement Learning: An Introduction, MIT Press, Cambridge, MA (1998) kap. 1-7
- Hanna Kokko: Modelling For Field Biologists: and Other Interesting People. Cambridge University Press (2007) (kap. 1, 2, 7, 8)
- Leah Edelstein-Keshet: Mathematical Models in Biology. SIAM (2005) (kap. 4.1, 4.2, 6.1-6.3)
- David J. Sweatt: Mechanisms of memory, Elsevier Academic Press, 2003 kap. 1
- Melanie Mitchell: An Introduction to Genetic Algorithms, MIT Press, 1996 (kap. 1-4)
- David E. Goldberg: Genetic Algorithms in Search, Optimization and Machine Learning. (kap. 1-4)
- Alternativní ke GA: Zbigniew Michalewicz: Genetic Algorithms + Data Structures = Evolution Programs (základy kap 1, 4; teorie kap 2-3; pokročilé a aplikace kap 8, 10, 12, 13)
- Alternativní ke GA: John H. Holland: Adaptation in Natural and Artificial Systems (základy: kap 1-2; teorie: kap 4-5)
- Steve Rabin (ed.): AI Game Programming Wisdom I, Charles River Media, 2002 (k. 4.3)
- Steve Rabin (ed.): AI Game Programming Wisdom IV, Charles River Media, 2008 (k. 2.2, 2.3, 2.5, 2.6)
Ostatní
- Donald L. DeAngelis and Wolf M. Mooij: INDIVIDUAL-BASEDMODELING OF ECOLOGICAL AND EVOLUTIONARY PROCESSES. In: Annu. Rev. Ecol. Evol. Syst. 2005. 36:147–68
- Text k virtuálním lidem - dizertační práce dr. Broma (kap. 1, 3, 4.1 - 4.5, 7)
- SOAR homepage (tutorial, dokumentace)
- Craig W. Reynolds - Not Bumping Into Things (něco k steeringu a obstacle avoidance)
- [3] - Něco k motion planning, hledání cest, atd.
Architektura autonomního agenta[editovat | editovat zdroj]
Základní definice[editovat | editovat zdroj]
Neexistuje bohužel všeobecně přijímaná definice toho, co to je (inteligentní) agent. Zajímavým zdrojem v této otázce budiž článek Is it an Agent, or just a Program?: A Taxonomy for Autonomous Agents. Nicméně existuje určité vymezení, na kterém se autoři schodují:
Inteligentní agent[editovat | editovat zdroj]
- Jedná se o entitu existující v nějakém prostředí (ať už skutečném, nebo virtuálním), které je agent schopen vnímat pomocí senzorů a ovlivňovat pomocí efektorů, přitom musí být agent schopen autonomně vybrat akci, kterou následně provede, a to tak, aby pokud možno dosáhnul zadaných cílů a dostatečne a adekvátně reagoval na případné změny v okolním světě.
Důležitá je autonomie (tzn. autíčko na dálkové ovládání ani obecně objekt v nějakém programu definici nesplní), působení v rámci nějakého světa, reaktivita (schopnost reagovat na změny) a proaktivita (nestačí pouze reflexivní chování, agent vykazuje nějaké složitější chování vedoucí k určitému cíli, je schopen sám se ujmout iniciativy).
Existují i další, příbuzné pojmy:
Avatar[editovat | editovat zdroj]
Virtuální bytost řízená člověkem
Virtuální člověk[editovat | editovat zdroj]
- Virtuální člověk je počítačový model performativní, behaviorální stránky určitého člověka. Jeho nutnou součástí je virtuální tělo. Tělo je součástí virtuálního světa, které je modelem přirozeného lidského prostředí. Tento svět je většinou dynamický, nedeterministický a pouze částečně pozorovatelný. Tělo je většinou zobrazeno graficky. Virtuální člověk vykonává sekvence akcí. Akcí se obvykle rozumí takový proces, jenž může provádět člověk, jenž trvá řádově několik desítek milisekund až prvních jednotek sekund a který většinou interpretujeme jako uzavřený celek. Akce nemodelují lidské mentální, ani fysiologické procesy.
- Virtuální člověk je komplexní. To znamená zaprvé, že umí vykonávat větší počet úkolů, z nichž některé jsou konfliktní, minimálně dva. Za druhé, že jeho tělo modeluje celé lidské tělo.
Rozdíl oproti inteligentnímu agentu spočívá v tom, že u virtuálního člověka není vyžadována autonomie. Tedy ač je často žádoucí, aby virtuální lidé navenek vykazovali určitou míru autonomie (např. ve virtuálních simulacích), ve skutečnosti mohou být všichni řízeni nějakou centrální jednotkou. Na druhou stranu agent nemusí mít podobu a tělo člověka.
Animat[editovat | editovat zdroj]
- Syntetická bytost žijící ve virtuálním prostředí, má tělo, které podléhá pravidlům (např. fyzikální model) platným v daném světě a pomocí kterého animat může se světem interagovat.
Jedná se o širší pojem, než je virtuální člověk; může jít o model v zásadě jakéhokoli živočicha. Častou jsou animati konstruováni za účelem pochopení fungování živých organismů, ověřováním ekologických a etologických hypotéz, nikoli za účelem prosté imitace; narozdíl od virtuálních lidí. (Neformálně řečeno Virtuální lidé jsou věrohodní „zvenku“, animati „zevnitř“ )
Bot[editovat | editovat zdroj]
- Bot je počítačem řízená umělá bytost, která simuluje postavu hráče v počítačová hře (obvykle se jedná o akční typ hry FPS). Boti mají tělo, podléhající zákonitostem virtuálního světa, a využívají předprogramované prostředky umělé inteligence vhodné pro daný typ hry, mapu a pravidla hry (Deathmatch, CTF).
Boty lze v zásadě chápat jako podtyp virtuálních lidí, ovšem s tím, že tyto herní postavy mají často podobu robotů či zvířat s antropomorfními rysy (což většinou nemývá vliv na mechanismus jejich řízení).
Prostředí[editovat | editovat zdroj]
- plná / částečná pozorovatelnost
- statické / dynamické
- deterministické / nedeterministické
- diskrétní / spojité
- jedno- / multi-agentní
- realtime / step-based
- epizodické / neepizodické
Abstraktní architektura agenta[editovat | editovat zdroj]
Agent přijímá vjemy a jeho chování je plně určeno posloupností všech vjemů, které kdy přijal. Formálně lze psát:
- S = {s1, s2, ... } je množina všech možných stavů prostředí
- A = {a1, a2, ... } je množina všech akcí, které může agent provést
- agent je reprezentován funkcí action: S* → A (neboli na základě posloupnosti stavů světa vybere akci)
- (nedeterministické) chování prostředí lze modelovat funkcí env: S x A → P(S)
Prostředí ale typicky není plně pozorovatelné, agent vnímá svět pomocí senzorů. Je potřeba přidat funkci mapující svět na množinu perceptů P a upravit funkci action:
- see: S → P
- action: P* → A
Toto je abstraktní matematický model agenta, pro skutečnou konstrukci agenta však nepoužitelný (není k dispozici nekonečný prostor pro zachycení všech možných posloupností vjemů).
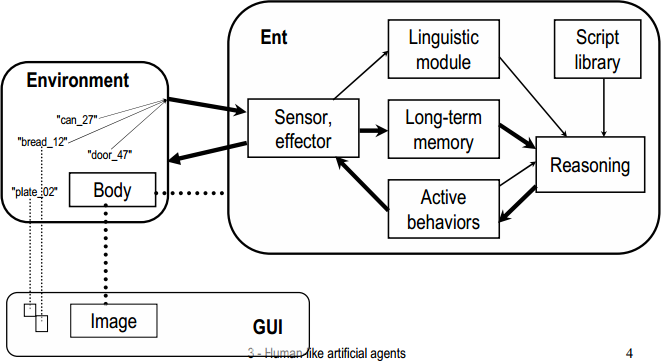
Percepce a paměť[editovat | editovat zdroj]
viz slajdy č. 8 (Representation) k Umělým bytostem
- reprezentace logickými fakty + RETE algoritmus ([4])
- afordance, smart objects
- objekty samy nabízí činnosti, jaké s nimi lze dělat, případně napovídají další akce potřebné pro komplexnější aktivity
- problémy: otevírání konzervy otvírákem, tanec v páru, objekty musí nabízet různé akce různým agentům
- role-passing - pro různé činnosti mám specializované role svázané s daným objektem v prostředí
- deiktická reprezentace - v paměti agenta uchovávám jen objekty, které se týkají činnosti, kterou děláma a to formou ukazatele pojmenovaného podle role, jakou objekty mají v dané činnosti (http://www.cse.iitm.ac.in/~ravi/papers/Vimal_IJCAI_07.pdf)
Vysvětlení pojmů:
- affordance: “The affordances of the environment are what it offers the animal, what it provides or furnishes, either for good or ill.” Affordances are resources that the environment offers any animal that has the capabilities to perceive and use them. (https://edisk.fandm.edu/tony.chemero/papers/adaptivebehavior07.pdf)
Paměť[editovat | editovat zdroj]
stručný výtah z Mechanisms of memory
Paměť člověka
- Deklarativní (explicitní) - fakta, události
- Nedeklarativní (implicitní)
- procedurální paměť (rutina, návyky)
- priming
- klasické (asociativní, Pavlovské) podmiňování
- neasociativní učení
Struktura paměti (jiné dělení) - dělení dle učení, paměti (storage) a vyvolání vzpomínky (recall), vše vědomé nebo podvědomé (conscious, unconscious)
- podvědomé učení, podvědomá paměť
- vědomé vyvolání
- trace conditioning (podobné jako Pavlovské podminování, ale mezi stimuly (zvoneček a jídlo) je časová mezera, využívá jiné okruhy v mozku než PP, specielně hippocampus)
- operant conditioning (jako PP, ale je vyžadována motorická reakce místo reflexu)
- paměť na chutě
- podmíněná averze k chutím (jednou sním v dětství zkažené maso a můžu být celý život vegetarián, protože mi maso nikdy nebude chutnat)
- kontextově podmíněný strach
- podvědomé vyvolání
- neasociativní učení - habituace, senzitizace, dishabituace
- asociativní učení - Pavlovské podmiňování, podmíněné mrkání, podnětově podmíněný strach
- motorické učení
- vědomé vyvolání
- vědomé učení, podvědomá paměť, vědomé vyvolání
- deklarativní učení
- prostorové učení
- vědomé asociativní učení
- pracovní paměť - vědomé učení, paměť i vyvolávání
- vizuálně-prostorový buffer
- epizodický buffer
- fonologická smyčka
Metody pro řízení agentů, řídící architektury[editovat | editovat zdroj]
- řídící architektury podle Wooldridge (deliberativní-založené na odvozování; reaktivní-behaviorální; hybridní)
- symbolické a konekcionistické reaktivní plánování
- hybridní přístupy (Belief Desire Intention, Soar)
- srovnání s plánovacími technikami: klasické plánovací techniky těžko použitelné, potřebují svět deterministický, statický a plně pozorovatelný, autonomní agent se povětšinou pohybuje ve složitějším světě
Řídící architektury podle Wooldridge[editovat | editovat zdroj]
Čistě reaktivní agent[editovat | editovat zdroj]
Vyznačují se jednoduchou přechodovou funkcí $ action: S \rightarrow A $, tzn. akce závisí pouze na aktuálních vjemech (agent nemá paměť).
Agent se stavem[editovat | editovat zdroj]
Akce je určená aktuálním stavem: $ action: I \rightarrow A $, stav se mění na základě vjemů $ see: S \rightarrow P $ a předchozího stavu: $ next: I \times P \rightarrow I $
Deductive reasoning[editovat | editovat zdroj]
Agent jako dokazovač (deliberate agents)[editovat | editovat zdroj]
Stavy agenta = databáze faktů. Akce jsou kódovány jako predikáty $ Do(A) $, kde $ A \in actions $. Chování agenta je realizován odvozovacími pravidly tvaru implikace. Rozhodování pak má podobu dokazování. Vybere se akce, pro kterou je dokazatelné $ Do(A) $. Když taková neexistuje, vybere se taková, pro kterou není dokazatelné $ \neg Do(A) $
Practical reasoning[editovat | editovat zdroj]
Skládá se ze dvou částí:
- deliberation - rozhodování, čeho chci dosáhnout.
- means-ends reasoning - plánování, jak toho dosáhnout.
Postavené na trojici beliefs - desires - intentions
Beliefs - domněný stav světa.
Intentions - stav mysli vyjadřující záměr něčeho dosáhnout. Řídí means-ends reasoning, přetrvávají (typicky dokud nejsou naplněné nebo se zásadně nezmění podmínky tak, že není racionální se jich nadále držet), omezují následující deliberation (na možnosti konzistentní se záměry), mají vliv na budoucí beliefs (věřím, že intentions naplním a podle toho se změní svět).
Desires (options) - budoucí možnosti agenta.
Abstract interpreter[editovat | editovat zdroj]
do // generate new possibilities options ← option-generator ( events, B, D, I ) // select the best opportunities to perform selected-options ← deliberate( options, B, D, I ) // adopt a selected opportunity as a subintention, or execute its actions I ← I ∪ selected-options[non-atomic] execute( selected-options[atomic] ) get-new-external-events( ) drop-successful-goals( B, D, I ) drop-impossible-goals( B, D, I ) until quit
Reactive reasoning[editovat | editovat zdroj]
Agent neplánuje nic dopředu, reaguje pouze na vnitřní stav a nový vjem. Inteligence je simulována pomocí přímé interakce se světem.
If-then pravidla[editovat | editovat zdroj]
- simple reactive planning - if-then pravidla s prioritou, co pravidlo, to konkrétní akce
- simple hierarchical planning - pod každým pravidlem může být akce nebo sada subpravidel (např. top-level goals, subgoals, tasks, atomic actions)
Konečné automaty[editovat | editovat zdroj]
"Rozšířená if-then pravidla", eliminuji spaghetti návrh
- finite-state machine - konečný automat, ke každému stavu je asociovaný kód a přechodová funkce. Agent vykonává akce podle kódu v aktivním stavu.
- hierarchical FSM - konečný automat s přechodovou funkcí mezi stavy. Ve stavu je buď kód nebo další konečný automat.
- probabilistic FSM - FSM, přechodová funkce může obsahovat pravděpodobnost přechodu (za daných podmínek)
Subsumpční architektura[editovat | editovat zdroj]
Hybrid reasoning[editovat | editovat zdroj]
Kombinují reaktivitu s plánováním, případně dalšími elementy
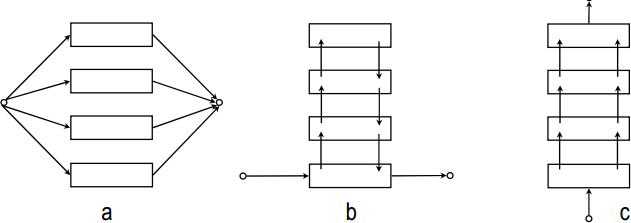
Vrstevnaté architektury[editovat | editovat zdroj]
- horizontální (a) - všechny vrstvy se rozhodují samostatně a dávají návrhy akcí. Jednoduché, ale může vést k nekoherentnímu chování. Je třeba mediátor, který vybírá, která vrstva má zrovna kontrolu. Mediátor je centralizovaný prvek, který může představovat bottlenect systému.
- vertikální - vrstvy si předávají nabízené akce, méně flexibilní, náchylnější k chybným rozhodnutím v jednotlivých vrstvách
- jednoprůchodové (c)
- dvouprůchodové (b)
BDI architektura[editovat | editovat zdroj]
BDI architektura je založená na practical reasoning, ale vyznačuje se jistými specifiky:
- means-ends se obvykle nevykonává, místo toho jsou k jednotlivým intentions předpočítané plány v podobě uložených struktur
- používá intentional stack - krom intentions přijatých na základě deliberation přijímám i subintentions jejich plánů
Pozn: https://www.aaai.org/Papers/ICMAS/1995/ICMAS95-042.pdf - paper, který doporučoval Neruda.
SOAR[editovat | editovat zdroj]
Algoritmus[editovat | editovat zdroj]
- Input phase - inputs are stored in the working memory
- Proposing phase - various if-then rules propose what to do next
- if-then pravidla matchují pouze pracovní paměť, v které jsou uložené všechny informace (struktura viz slajdy "Soar intro").
- používá RETE algoritumus
- střílející pravidla vytváří dočasné struktury v paměti a nabízí operátory.
- Decision phase - just one proposal is chosen
- výběr mezi nabízenými možnostmi
- může nastat impass (žádné pravidlo nestřílí, více neporovnatelných pravidel, nelze aplikovat operátor), řešení: nový stav (jak přesně to funguje? Spustím nějaké klasické plánování?) + zapamatuji si řešení v dlouhodobé paměti
- Applying phase - new internal symbols or motor symbols are created by an if-then rule
- vybrané pravidlo vytvoří trvalou strukturu v paměti
- obvykle jen kopíruje akci vybraného operátoru do output-link
- Output phase - motor symbols are interpreted and the state of the environment is changed
Central cognitive system[editovat | editovat zdroj]
The architecture involves
- a programming language
- a working memory (symbols -"variables")
- a long-term memory (if-then rules)
- a learning
Symbolické a konekcionistické reaktivní plánování[editovat | editovat zdroj]
Obrázky ze slajdů Cyrila Broma (zveřejněno s jeho svolením)
Symbolické plánování[editovat | editovat zdroj]
Konekcionistické plánování[editovat | editovat zdroj]
Srovnání s plánovacími technikami[editovat | editovat zdroj]
Jde o:
- algoritmy hledání cesty (A* apod)
- plánovací techniky využívající dokazování v predikátové logice
- plánování v prostoru stavů/plánů
(viz slajdy z UI 1)
Klasické plánování má tyto problémy:
- není any-time - časté přeplánovávání v dynamickém světě vede k problémům
- vyžaduje plně pozorovatelný svět
[editovat | editovat zdroj]
Pokud máme agenta, který se má pohybovat v nějakém prostředí, je třeba řešit problém navigace. Různá řešení závisí na tom, jaké informace máme k dispozici:
- Známe mapu prostředí?
- Známe svou pozici na mapě?
- Známe pozici cíle/směr k cíli?
[editovat | editovat zdroj]
Pokud neznáme mapu prostředí, musíme se řídit podle jednoduchých navigačních pravidel. Příkladem jsou Bug algoritmy, které předpokládají, že agent zná pouze směr k cíli a dovede v každém okamžiku zjistit, jak je od cíle daleko.
- Bug1 - označí si hitpoint a leavepoint pokud narazí na překážku. Musí ji objet celou.
- Bug2 - označí si hitpoint a objíždí, dokud nenarazí na průsečík s přímkou k cíli, který je blíž než hitpoint.
Vizualizace algoritmů: https://www.youtube.com/watch?v=YVuxvHQiLb0 Slajdy s obrazky priklady a protiprikladu: http://www.cs.cmu.edu/~motionplanning/lecture/Chap2-Bug-Alg_howie.pdf
Reprezentace terénu[editovat | editovat zdroj]
Vytvoření mapy navigačních bodů nebo oblastí. Poté se problém převede na hledání cesty v grafu. Přístupy:
- graf viditelnosti
- Voronoi diagramy
- lichoběžníková dekompozice
Podrobneji: http://robotika.cz/guide/exactplan/cs
[editovat | editovat zdroj]
Máme tedy nějakou hru s mapou terénu. Chceme použít A* algoritmus pro pohyb agenta mapou. Jednou možností je, že autoři hry do mapy ručně dají waypointy, což jsou body na mapě, kam bot může jít. Navigaci pak uděláme tak, že ze současné pozice bota (nemusí být na žádném waypointu) hledáme spojnici k nejbližšímu waypointu (těch waypointu může být opravdu hodně na mapě, pokud jich tam není dost, tak se může stát, že se bot prostě zasekne o něco, když se k waypointu snaží dostat) a pak spustíme A* algoritmus, tak jak ho známe z UI.
Waypointy jdou nahradit navigation mashem (navmash zkráceně), což je technika, která rozdělí mapu na konvexní polygony. V konvexním polygonu vede z libovolného bodu do libovolného jiného bodu cesta, která je přímkou. Použitím navmashů se typicky sníží čas, který potřebuje A* na nalezení cesty, protože se zmenší počet uzlů, se kterými A* musí počítat.
Pozn: http://udn.epicgames.com/Three/NavigationMeshReference.html - Rozdíl mezi waypoints a navigation mashes na obrázku.
Materiály[editovat | editovat zdroj]
- http://artemis.ms.mff.cuni.cz/main/download/hagents/H-likeAgents4_Bajer060410.pdf - slajdy, které používá Brom
- http://harablog.files.wordpress.com/2009/06/beyondastar.pdf - Zřejmě zdroj předchozích slajdů. Velmi pěkně zpracované.
Poznámka[editovat | editovat zdroj]
Určitě si nastudujte steering a obstacle avoidance. Patří sem i A*, LPA*, "rozdlaždicování" terénu (od dlaždic, šestiúhelníků, jejich hierarchických variant až po obecné polygony), waypointy atd. (experimentálně ověřeno, že na zkoušku je to dobré vědět :-) )
Komunikace a znalosti v multiagentních systémech, ontologie, problém omezené racionality, Kripkeho sémantika možných světu.[editovat | editovat zdroj]
- http://ssdi.di.fct.unl.pt/mas/0910/slides/7.pdf - tyto slajdy vypadaji jako vytah z Wooldridge, kde je komunikace popsana pekne
- KIF (Knowledge Interchange Format)
- KQML
- Ontologie velmi označuje terminologii. Agenti spolu komunikují pomocí zpráv (například pomocí KQML) a ve zprávách se právě uvádí jako jedna z hlaviček zpráv právě ontologie, takže když se agenti baví například o rozměrech součástek pro auto, tak vědí, co který pojem přesně znamená a budou vědět, že oba agenti pracují se stejnými fyzikálními jednotkami.
Kripkeho model možných světů[editovat | editovat zdroj]
viz Wooldridge - 12. kapitola (Logic for Multiagent Systems) + http://ktiml.mff.cuni.cz/teaching/files/materials/A1_1.pdf
Problém omezené racionality[editovat | editovat zdroj]
Každý agent, který se má racionálně rozhodovat v komplexním prostředí podléhá následujícím omezením:
- v daném okamžiku disponuje pouze omezenou informací o světě (např. vidí jenom na omezenou vzdálenost)
- má pouze omezené prostředky ke zpracování informací (např. RAM,CPU)
- musí se rozhodovat v omezeném čase (pokud jde o real-time agenta)
V konečném důsledku je pro takového agenta nemožné se rozhodovat racionálně (tzn. volit vždy optimální akce). Musí se tedy spolehnout na heuristiky a omezenou znalost prostředí.
Etologické motivace, modely populační dynamiky.[editovat | editovat zdroj]
Modely populační dynamiky[editovat | editovat zdroj]
Zdroje:
- http://nrich.maths.org/7252
- (Cyrilovy slajdy) http://artemis.ms.mff.cuni.cz/main/download/hagents/10_3a_H-likeAgentsEtologie_100318.pdf
Analytické modely[editovat | editovat zdroj]
Analytické modely představují nástroj matematické biologie ke zkoumání vývoje populací nejrůznějších živých organismů. Sestavují se na základě empirických dat (z pozorování). Analytický model je zpravidla tvořen diferenciálními rovnicemi, které popisují chování systému. Jejich nevýhodou je, že bývají příliš obecné.
Příklad: jednoduchá rovnice pro jednu populaci ($ t $ - čas, $ b $ - birth rate, $ d $ - death rate):
$ N(t+\Delta t) = N(t) + b*N(t)*\Delta t - d*N(t)*\Delta t $
Existují složitější modely, které lépe modelují konkrétní prostředí a pomáhají zodpovědět otázky jako např. Za jak dlouho dojde k vyhubení chráněného živočicha XY?
Existují také modely pro chování více populací (model predátor-kořist, hostitel-parazit apod.).
Simulační modely[editovat | editovat zdroj]
Simulační modely jsou založeny na umělých agentech zvaných animati, kteří jsou plausibilní - chovají se realisticky. Hlavní nevýhodou simulačních modelů je vysoký počet parametrů.
Metody pro učení agentů; zpětnovazební učení, základní formy učení zvířat[editovat | editovat zdroj]
Předpokládejme agenta, který se má naučit nějakou funkci $f: Input \rightarrow Output$. Učení agentů se využívá především tam, kde nelze pokrýt všechny možné eventuality tím, že je do agenta naprogramujeme předem.
Při strojovém učení potřebujeme vědět:
- Jakou část agenta zlepšujeme? (př. rozhodovací mechanismus pro výběr akcí)
- Jakou odezvu má agent k dispozici? (př. žádnou, otagovanou trénovací množinu)
- V jaké podobě ukládáme naučená data? (př. rozhodovací strom, pravděpodobnostní rozdělení, sada pravidel)
Základní dělení metod strojového učení:
- S učitelem - máme: $ (x_1,y_1),\ldots,(x_n,y_n) $ a chceme: $ f(x_i)=y_i $
- Bez učitele - máme: $ \vec{x_1},\vec{x_2},\ldots,\vec{x_n} $ a chceme: $ P(X=\vec{x}) $
- Zpětnovazební učení - máme: $ s_0,a_1,s_1,a_2,\ldots $ kde některé stavy mohou být odměněny a chceme $ \Pi(s_i) $ - nějakou sadu pravidel co dělat ve kterém stavu abychom posbírali co nejvíc odměn.
Učení s učitelem (supervised learning).[editovat | editovat zdroj]
Je metoda, při které se používá následující schéma:
- Vezmeme data (množina dvojic (vstup,výstup) - $ \lbrace(x_1,y_1),(x_2,y_2),\ldots,(x_n,y_n)\rbrace $) a rozdělíme je na
dvě disjunktní množiny: trénovací ($ T $) a testovací ($ E $). Pro hledanou funkci $ f $ platí: $ \forall i:\ f(x_i)=y_i $
- Použijeme nějaký učící algoritmus, pro nalezení hypotézy $ h $, která aproximuje trénovací data.
O hypotéze řekneme, že je konzistentní s množinou trénovacích dat $ T $, pokud platí:
$ \forall (x_i,y_i)\in T:\ h(x_i)=y_i $
- kvalitu řešení (tj. nalezenou hypotézu $h$) otestujeme na množině testovacích dat $ E $. Čím menší je suma $ \Sigma_{(x_i,y_i)\in E}|h(x_i)-y_i| $ tím lepší hypotézu jsme našli.
Pokud je obor hodnot hledané funkce diskrétní, jde o klasifikaci. Je-li obor hodnot spojitý, jde o regresi.
Učení bez učitele (unsupervised learning).[editovat | editovat zdroj]
Je metoda, při které se agent snaží ze vstupních dat odvodit nějaké zákonitosti (nemá při tom k dispozici správné výstupy a tímpádem ani zpětnou vazbu). To co se agent učí je pravděpodobnostní model vstupních dat, na základě kterého potom může klasifikovat nová data. Př. Bayesovské učení, EM algoritmus
Zpětnovazební učení[editovat | editovat zdroj]
Zpětnovazební učení je metoda, při které se agent učí, jak má volit akce, aby našel optimální strategii pro dané prostředí. Jde o učení bez učitele. Agent sice dostává odezvu, ale přímo z prostředí, takže musí experimentovat, a zjišťovat, které stavy jsou dobré a které špatné. Něco jako, když hrajete hru, jejíž pravidla neznáte a po cca. 100 tazích Váš oponent řekne: "Prohráls saláte!".
Řeší se zde problém explorace vs. exploatace. Pokud agent zkouší nové akce, jejichž výsledek nezná, jde o exploraci, pokud provádí akce, o kterých ví, že mu přinášejí užitek, jde o exploataci. Problém je, že optimální strategie nemůže být ani čistě explorační ani čistě exploatační - hledá se vyvážený kompromis.
- Pasivní učení - agent má pevně danou strategii a učí se, jak jsou ohodnocené jednotlivé stavy, do kterých se dostane.
- Aktivní učení - agent se učí jaké akce má volit a zároveň jak jsou ohodnocené.
Základní formy učení zvířat[editovat | editovat zdroj]
- Habituace - úbytek reakce na opakování téhož podnětu (přitom je reakce na jiné podněty zachována - nejde tedy o únavu) - když na chování je reakce co má minimální dopad na zvíře, tak to chování vymizí (třeba zvířata co si zvyknou, že lidi nejsou predátoři)
- Senzitizace - nárůst reakce na určitý podnět (opak habituace) - když zvíře má silný zážitek, tak si s chováním asociuje tuhle emoci (ať už špatnou nebo dobrou)
- Imprinting - proces učení vázaný k určité fázi vývoje jedince, který vede k trvalým a nezvratným změnám chování (kachny a Konrad Lorenz) - první věc co právě narozené zvíře vidí si imprintuje jako matku
- Klasické podmiňování - Pavlov a jeho psi. Nepodmíněný podnět - sám vyvolává reakci, podmíněný podnět - vyvolává reakci až když je spojen s nepodmíněným podnětem. Když psi dostávají jídlo a zároveň zvoníme zvonkem, časem si asociujou, že když zvoníme zvonkem tak dostanou jídlo.
- Operantní podmiňování - Chování zvířete upevňujeme nebo oslabujeme za pomocí stimulací jako následků jeho chování. Zároveň používáme stimulus jako předchůdce chování - trigger pro chování (povel sedni). Typy následků: pozitivní a negativní posilování (reinforcement) a tresty. Pozitivní posilování chování je nejtypičtější - jednodušše odměníme zvíře když dělá to co chceme. Negativní posilování funguje tak, že v prostředí je konstantně nějaký nepříjemný vjem a když zvíře dělá to co chceme tak se vjem odstraní. Rozdíl oproti trestu je jasný, trest zvířeti dá nový negativní vjem, chování oslabuje. Pozn. Chaining - učíme sled chování, jakože psa chceme naučit, aby sedl, lehl, zatancoval a zaštěkal. Princip je ten, že psovi dáváme sérii povelů a odměňujeme ho až nakonec.
Umělá evoluce; genetické algoritmy[editovat | editovat zdroj]
- Základní přístupy a pojmy: populace, fitness, rekombinace, genetické operátory; dynamická vs. statická selekce, mechanismus rulety, turnaje, elitismus
Evoluční teorie: Jedinci přežívají v závislosti na tom, jakou šanci mají se reprodukovat.
Genetika: Genenetický kód jedince určuje jeho fenotyp (to jak se chová v prostředí). Při reprodukci jedinců probíhá rekombinace genetického kódu. Taky jsou možné malé mutace.
Umělá evoluce:
- Ve srovnání s přírodní - problém reprezentuje prostředí evoluce, potencionální řešení reprezentují jedince, kvalita řešení reprezentuje šanci jedince na reprodukci.
- Umělá evoluce prohledává prostor potencionálních řešení problému. Neprohledává ho náhodně, směr prohledávání určuje kvalita řešení. Zároveň to není hill climbing, protože si uchováváme variabilitu řešení v množině řešení - populace.
Schéma evolučního algoritmu:
- Začneme s počáteční množinou přípustných řešení - populace
- Iterujeme:
- Selekce rodičů - z populace vybereme pomocí kvality jedinců rodiče pro reprodukci
- Křížení a mutace - rekombinujeme rodiče do jejich dětí, děti navíc mutujeme.
- Selekce populace - pomocí kvality jedinců v populaci rodičů a dětí vybereme novou populaci.
- Iterujeme dokud nemáme dost dobré řešení.
Genetický algoritmus: Evoluční algoritmus co kóduje jedince pomocí jejich genu - binárně zakódovaného jedince. Navíc máme fitness funkci, určující kvalitu daného jedince (může to být analyticky, nebo i simulací).
Kódování jedince: Pokud máme jednoznačné diskrétní kódování, tak většinou není problém kódovat přímo tak, jak bychom jedince uložili v počítači. Problém nastává při ukládání integer a reálných čísel (mantisa exponent). Mutace co se strefí do exponentu případně do signifikantního bitu mají obrovský dopad na uložený parametr. Obecně si musíme dávát pozor na to, aby byly mutace upravené tak, že změny jsou 'uniformí', nebo upravit kódování tak, že se to nestane.
Např. Když optimalizujeme reálné parametry nějaké spojité funkce, tak je nebudeme ukládat binárně. Když ale budeme řešit problém Batohu, tak si jedince můžeme uložit jako vektor 1/0 kde 1 znamená, že předmět jsme dali do batohu.
Křížení:
- jednobodové, vícebodové křížení - vezmeme dva geny rozdělíme je na několik kousků podle stejných bodů a pak kousky prohodíme
- další viz. https://en.wikipedia.org/wiki/Crossover_(genetic_algorithm) a speciální podle aplikace
- křížení pro permutace - seznamy jsou permutace (seznam měst v TSP), tak na to musí být speciální operátory křížení
Mutace:
- bit flip - s pravděpodobností m bit flipnem
- gausovské - reálná čísla mutujeme přidáním čísla z náhodného rozdělení, případně přičtení celého čísla z gausiánu pro integery
- specifické pro daný problém - např když řešíme batoh, tak bychom třeba chtěli aby mutace nepřeplnila batoh, nebo aby něco vyndala z batohu a dala do něj něco jiného
Selekce:
- ruletová selekce - každý jedinec dostane políček rulety úměrné jeho fitness, pak zatočíme ruletou tolikrát kolikrát potřebujem
- turnajová selekce - náhodně volíme jedince do 'turnaje' kde vyhraje ten, co má vyšší fitness s pravděpodobností $ \phi $
- stochastic universal sampling - ruletová selekce je moc RNG, uděláme ruletu jako v selekci ale zatočíme ruletou vždy o stejný úhel - suma fitness / počet jedinců do populace. Výhoda je, že nadprůměrní jedinci mají zaručený postup, očekávaný počet reprodukcí je pro vysoké fitness mnohem předvídatelnější.
Reprezentační schémata, hypotéza o stavebních blocích.[editovat | editovat zdroj]
viz Mrazovy slajdy
Jedinec: binární řetězec {0,1}
Schéma: binární řetězec {0,1,*} - * wildcard za 0/1. Schéma je kód množiny jedinců.
- řád schématu S - o(S) - počet 0/1 v řetězci
- definující délka schématu S - d(S) - vzdálenost mezi první a poslední 0/1 (ořízneme schéma o * a co nám zbyde má délku d)
- fitness schématu S - F(S) - průměrná fitness odpovídajících jedinců v populaci (!!! důležité, není to průměr přes celou množinu schématu)
Věta o schématech (stavebních blocích): Krátká nadprůměrná (z pohledu fitness) schémata s malým řádem se v populaci během GA množí exponenciálně.
Co to znamená, schéma co je krátké má větší šanci přežít během křížení, stejně tak ty s nízkým řádem. Ty schémata co mají vysokou fitness jsou navíc vybírány do další generace.
Důkaz: Nástin - ne úplně formálně, muselo by se přesně definovat hodně věcí, co pak v praxi stejně budou jinak. Máme populaci P(t) v čase t, populace velká n, jedinec dlouhý m. Definujeme C(S,t) jako počet jedinců v P(t) co matchují na schéma S. Potřebujeme odhadnout poměr mezi C(S,t) a C(S,t+1) v závislosti na vlastnostech schématu. Počet jedinců schématu v populaci se mění během: selekce, křížení a mutace. Během selekce, počet vybraných jedinců je úměrný F(S)/F(t) kde F(t) je průměrná fitness populace. Během jednobodového křížení šance, že jedinec vypadne ze schéma je d(S)/(m-1) (pokud teda oba rodiče nejsou v S). Nakonec mutace má šanci se trefit na pevnou pozici v schématu p^o(S). Když se to pronásobí tak to vyjde že krátká, nadprůměrná, malý řád schémata se budou množit jako $ C(S,t+1)\geq C(S,t)*\lambda; \lambda\geq F(S)/F(t)*(1-p_{cross}d(S)/m)-p_{mutate}o(S)) $ což je exponenciální pro ty schémata, pro které jejich fitness vyváží to, jak pravděpodobné je že jedinci fitness nepřežijou do další generace.
Důsledky Jelikož F(S) záleží na populaci, tak se nám schémata nepropagují často tak, jak by měly. Příklad populace: {1000,0001,0110,0000}, cíl 1111, fitness počet 1, schéma 1*** a ***1 jsou průměrná ale F(1**1) je stejné jako F(0**0). Teoreticky by tedy měly obě tyto schéma zůstat v populaci stejně zastoupená.
GA aproximuje fitness mnohem víc schémat, než má jedinců. Ale ne všechny fitness jsou aproximovány dobře. Proto je potřeba výrazně větší populace, než je délka jedince (teoreticky třeba 2^m).
Genetické a evoluční programování[editovat | editovat zdroj]
Přijde mi jako dost málo obsáhlá otázka. Asi bych začal tím, že bych zadefinoval EA a možná i GA.
Jak GP tak EP jsou metody, kde evolvovaní jedinci jsou programy. Evoluční programování je EA na programech (nejtypičtější jsou konečné automaty), kde navíc neprobíhá křížení, jen mutace. Historicky jde o to, že se snažili evolucí vyvinout umělou inteligenci - tj nějaký řídící program. EP nekóduje jedince pomocí genu ale přirozeně, mohli bychom třeba evolvovat neuronové sítě, pak kódování neuronové sítě je nějaké pole hyperparametrů. Tohle se nám může hodit v případě, když třeba neumíme přesně definovat požadované výstupy, ale umíme přibližně ohodnotit program pomocí nějaké simulace.
Rozdíly mezi GA a EP:
- žádné omezení na reprezentaci jedince, můžeme mít i různě složité jedince (pak musí mutace být schopná jedince zesložitit)
- používá jen mutace a ty sledují následující pravidla: vysoké změny v chování (v následku mutace) jsou míň pravděpodobné než malé změny v chování, mutace zpomalují když se evoluce blíží k globálnímu optimu (tohle moc nevím jak toho dosáhnout, když nevíme co je optimum)
Genetické programování je jako EP, ale omezíme se na programy takového typu, že je jde dobře kódovat. Pak můžeme program zakódovat do genu a na tom pouštíme GA. Zásadní rozdíl od GA je, že jedinci nemají fixní délku, programy můžou mít různé délky. Typické kódování jedince je pomocí stromu operátorů (a*b+c ~ V=(a,b,c,*,+); E={(a,*),(b,*),(*,+),(c,+)}). Respektive jako programy v Lispu, případně různé funkcionální programy.
Příklad GP: Představme si, že potřebujeme naprogramovat automatického obchodníka s akciemi. Nějak si to formalizujeme, že obchodník má k dispozici nějakou množinu proměnných (časové řady cen akcií třeba) a musí rozhodnout jak obchodovat. Nadefinujeme si program jako nějaký lisp co z těch proměnných vrátí vektor čísel n které jsou kolik chce nakoupit/prodat akcií daného typu. Fitness takového programu můžeme spočítat na historických datech, jako kolik toho program vydělá. No pak si zadefinujeme křížení a mutace a můžeme pustit GA. Další příklady - naprogramování elektrického obvodu s danými vlastnostmi, kvantové počítače, další viz [5].
Pravděpodobnostní modely jednoduchého genetického algoritmu.[editovat | editovat zdroj]
viz slajdy typu eva09-2
- Geneticke operatory, pravdepodobnosti vyskytu a selekce jedincu a velikost jejich zastoupeni v populaci muzeme vyjadrit jako matice/vektory.
- Nekonecne populace muzeme modelovat jako dynamicky system a hledat jeho pevne body. Jake jsou vlastne nevime.
- Vyvoj konecnych populaci muzeme modelovat jako Markovovsky proces. Lze odvodit, ze bude konvergovat k chovani nekonecnych populaci.
Komentar Romana Nerudy k vyse uvedenemu:
kdybych to zkousel ja, asi bych chtel v zasade ten nadhled, co rikate, s durazem na to, jak se ty populace reprezentujou, t.j. u nekonecnych zavedeni vektoru cetnosti a pravdepodobnosti vyberu, neco o tom, jaky zobrazeni vlastne hledame, a co o nem muzeme rict, bez podrobnosti a dukazu, no a u konecnych zase porozumneni tomu, nad cim ten markovsky proces pracuje, co jsou stavy, jaky vyznam ma ta prechodova matice, ze je velika, a zase samozrejme ty konkretni slozite vzorecky ne, pamatovat se to neda a odvozuje se to nekolik desitek stranek. jeste jsem to asi nikdy nepolozil jako samostatnou otazku, vetsinou na to dojde rec v souvislosti s teorii schemat.
Koevoluce, otevrená evoluce.[editovat | editovat zdroj]
- Koevoluce - "biologické zbrojící závody", problém cyklení strategii (řešení turnaji s předchozími generacemi).
- Otevřená evoluce - příklad "Tierra" - jednoduché algoritmy, které vykonávají kód v omezené paměti; fitness počet jedinců
- Zdroj: Modelování evolučních procesů (Radek Pelánek)
Aplikace evolučních algoritmů[editovat | editovat zdroj]
- výber akcí, evoluce expertních systému, konecných automatu, adaptace evolucních pravidel, neuroevoluce, rešení kombinatorických úloh
Evoluce expertních systému (Michigan, Pittsburgh)[editovat | editovat zdroj]
Zdroje:
- slajdy Romana Nerudy k EVA2
- Introduction to Learning Classifier Systems (Dr. J. Bacardit, Dr. N. Krasnogor)