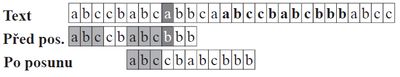Databázové modely a jazyky/DIS
Obsah
Databáze textů: modely (boolský, vektorový) (7×🎓)[editovat | editovat zdroj]
+ Vyhledávání v textech: boolské a vektorové indexy a indexace, usporádání odpovedí, signatury a jejich implementace
Přesnost a úplnost (Precission vs Recall)[editovat | editovat zdroj]
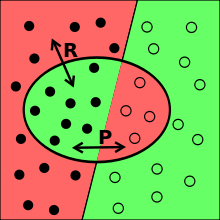
- $ P = \frac{\text{#vybraných relevantních záznamů}} {\text{#vybraných záznamů}} $
- $ R = \frac{\text{#vybraných relevantních záznamů}} {\text{#relevantních záznamů v souboru}} $
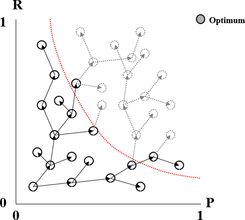
- 💡 závislost R a P je v praxi na hyperbole (zvětšující se P snižuje R a obráceně)
Boolský model DIS[editovat | editovat zdroj]
Každý dokument je popsán množinou termů, které obsahuje. Termy jsou uloženy v indexovém souboru a odtud potom probíhá vyhledávání.
Dotaz - vyraz obsahujici termy spojene logickymi spojkami ("AND", "OR", "NOT")
- Postupne doslo k nekolika rozsirenim: 1. vyhledavani viceslovnych spojeni; 2. test na metadata dokumentu (autor, rok vydani...) 3. pouziti wildcardu (?, *)
- Je mozne do dotazu zavest nove operatory (term1 sentence term2, term1 paragraph term2...).
- Proximitní omezení - operátory pro blízkost termů (věta, odstavec,...)
Nevyhody: všechny termy stejně důležité, nejde řadit vysledky dle relevance (pouze hrube: uzávorkováním OR, převodem na DNF, ...), obtizne se omezuje mnozina vysledku
Vyhody: snadna implementace (ma to uz 50 let), pouziti signatur pro rychlou eliminaci hromad dokumentu
Uspořádání odpovědi dle relevance[editovat | editovat zdroj]
- ve vektorovém modelu je to ok,
- u booleovského modelu je možné rozložit dotaz do DNF (disjunktně normální formy a ohodnotit jednotlivé výstupy podle toho, kolik je ne negovaných termů ve splňované podformuli)
- př.: kocka AND pes => (kocka AND pes) OR (kocka AND NOT pes) OR (NOT kocka AND pes).
Rozšíření booleovského modelu – lze pokládat vážené dotazy – např kocka (0,9) AND pes (0,3), dokumenty mají také ohodnocený vektor termů. Různé metody, liší se podle toho, jak je vypočítáván AND a OR, např. ve Fuzzy logice je AND minimum a OR maximum vah.
Indexování (boolský)[editovat | editovat zdroj]
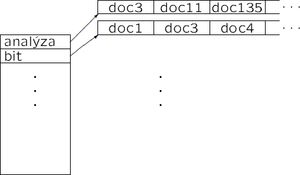
Organizace jako invertovaný seznam - pro každý term seznam dokumentů, termy jsou setřízené
- Indexy lze nad kolekcí dokumentů vytvářet dvojím způsobem. Buď je množina termů pevně daná a pro každý nový dokument se aktualizují jen indexy (řízená indexace), nebo se s každým novým dokumentem přidávají i nové termy (neřízená indexace).
- sestrojení: setridim dvojice (term, dokument) vnejsim tridenim a pak k nim sestrojim ten invertovany index
Vhodná předzpracování textu (indexu,dotazu):
- Lemmatizace - Přiřazení správného lemmatu jednotlivým slovům ( Základní tvar slova, Slovní druh, osoba, číslo, čas, vid, ... , Informace z větného rozboru - podmět,předmět, ... )
- Tezaurus - hierarchický strukturovaný slovník
- Př.: dotaz('operační systém') -> 'Windows','Linux'
- Stop-list - slovník nevýznamových slov (spojky, částice,...) ⇒ nevkládají se do indexu
- Určení termů - ručně (každý může určit jiné termy) vs automaticky (jednoznačné, ale bez porozumnění textu)
Signatury, metody implementace signatur (vrstvené kódování)[editovat | editovat zdroj]
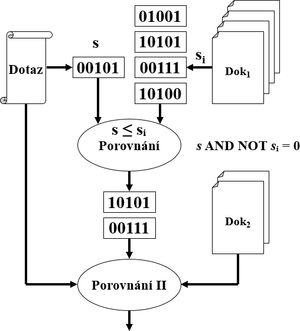
signatura dokumentu je k-bitový řetězec, který v sobě nese informaci o tom, které termy v dokumentu jsou
- pro konjunktivní dotazy nad boolským modelem (∀dokumentu se priradi signatura, dotazu taky) - 💡využívá se malá časová a prostorová složitost
- signatura dokumentu sᵢ vyhovuje signature dotazu s pokud sᵢ ≥ s (po bitech) tj. s AND NOT sᵢ = 0
- pokud nevyhovuje tak tam nejsou ∀hledane termy, pokud vyhovuje tak tam byt mohou
Přiřazení signatury slovu
- bitova mapa - signatury musi mit tolik bitu, kolik je termu.
- hashovaci fce - ktera priradi termu signaturu, jejiz bitovy zapis obsahuje prave jednu jednicku (pro 128bitove signatury tedy mame 128 moznych ruznych signatur jednotlivych termu). to se hodi pro vrstveni viz nize.
Přiřazení signatury dokumentu - je mozno 2 zpusoby (nebo jejich kombinaci):
- Vrstveni signatur - každý term má svou signaturu (vypočtenou pomocí hash funkce) dlouhou d bitů a signatura bloku = OR přes všechny signatury termů v bloku.
- 💡 Pri vrstveni vetsiho poctu signatur to ztraci na efektivite - moc jednicek (same jednicky vyhovuji kazdemu dotazu). Proto se dokumenty rozdeluji na bloky se samostatnymi signaturami. Při vhodném dělení, např. na rozhraní kapitol nebo odstavců, není ztráta informace příliš důležitá. Slova nacházející se daleko od sebe spolu obvykle nesouvisí
- Bloky se vytváří dvěma metodami: FSB (fixed size block) pro úseky s přibližně stejným počtem slov. FWB (fixed weight block) pro úseky s přibližně stejným počtem jedniček optimálně k/2 (stejne jednicek a nul).
- Řetezeni signatur - signatury se spojují do řetězce - vhodné pro strukturovaná data (autor, rok vydání, nakladatelství...)
Uložení signatur:
- Invertovany soubor - index organizovan pomoci signatur. Pro jednotlivé pozice v signaturách se udržují bitové sloupce. Pri porovnavani se signaturou dotazu se pak vezmou ty bitové sloupce, kde je v dotazu 1 a spustí se na nich bitové AND a mám bitový sloupec, kde tam, kde jsou jedničky, jsou potenciální hledané záznamy
- strom signatur - podle prefixů
| další info |
|---|
monotonni signatury - ma-li term t signaturu x, tak term tu (zretezeni termu t a termu u) ma signaturu v kazdem bitu >= signature x. Dobre pro nalezeni napr. sklonovanych slov pri zadani korene apod. Monotónní signatury lze vytvářet vrstvením signatur tzv. n-gramů (n po sobě jdoucích znaků) – např. pro trigramy by byla monotonni signatura slova „kocka“ – sig(„koc“) | sig(„ock“) | sig(„cka“)
Metody je možné různě kombinovat tak, aby výsledná struktura byla co nejefektivnější. |
| další zdroje |
|---|
|
|
Vektorový model DIS[editovat | editovat zdroj]
reprezentace dokumentu pomocí množiny VAH <0,1> termů
- mladší než boolský (asi o 20 let) a vznikl aby odstranil chyby boolského modelu - především díky možnosti ohodnotit termy jak v dotazu, tak v indexu
Dotaz - také vektor, shoda se vyhodnocuje skalarnim součinem obou vektorů (dokumentu a dotazu)
- protože dlouhé dokumenty by byly zvýhodněny (obsahují jistě více termů), provádí se normalizace vektorů, to lze provádět:
- během indexace, což nezvětšuje odezvu, je však zapotřebí občas vše znovu "přenormalizovat"
- během vyhledávání - zpomaluje odezvu, je v definici podobnostní funkce
- Lze termu priradit zapornou vahu a tim uprednostnit dokumenty, ktere jej neobsahuji.
- Ve vektorovovem modelu je snadne radit vysledky podle miry shody, pripadne orezat mnozinu vysledku nejakou minimalni hodnotou.
Indexace VDIS[editovat | editovat zdroj]
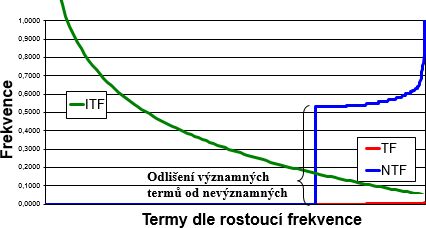
obvykle vychazi z (normalizovane) cetnosti vyskytu termu v dokumentu - čím víc, tim vyssi ma vahu
- založena na frekvenci termu (TermFrequency) v dokumentu $ TF = \frac{\text{#výskytů termu}} {\text{#∀termů v dokumentu}} $
- je potřeba vyřadit nevýznamová slova (stop list = {the, a, an, on ... })
- normalizovat frekvenci termů (kvuli malým TF)
- $ NTF_i = 0 $ pro $ TF_i < \epsilon $(💡 ignujeme termy s velmi nízkým výskytem)
- $ NTF_i = \frac{1}{2} + \frac{1}{2} * \frac{TF_i}{max_j(TF_j)} $, jinak
- NTF vzorec nám dostane hodnoty do int. {0} + ⟨1/2;1⟩
- Inverzní frekvence termu v dokumentech (důležitost termu v kolekci dokumentů, značí se IDF nebo ITF)
- $ IDF = -log\left(\frac{\text{#dok.obsahujících term}}{\text{#∀dok.}}\right) $
- 💡 vyjde IDF ∈ ⟨0 ; ∞⟩ (počítáme log₁₀ čisel mensich nez 1 ⇒ výsledek by byl záporný, proto ten minus)
- 💡 pro dotazování jsou nejvhodnější termy co se vyskytují v cca 1/2 dokumentů a nevhodná jsou slova vyskytující se ve většině dokumentů
- 💡 jde prakticky o použití vzorecku entropie tj. "obrácená hodnota" - čím je znak častější tím menší má entropii = tím méně informace nese
- def. Pokorný: $ IDF = log\left(\frac{\text{#∀dok.}}{\text{#dok.obsahujících term}}\right) + 1 $(def. Pokorný)
- 💡 Definice jsou v podstatě matematicky ekvivalentní, akorát ta od Kopeckého téměř eliminuje málo důležité termy
Váha termu i v j-tém dokumentu se urči jako $ w_{ij} = NTF_{ij} * ITF_j $
- Lze uplatnit i zpětnou vazbu, kdy uživatel označuje relevantní dotazy a DIS na to reaguje přehodnocením výpočtu.
Vyhledávání vzorku v textech (sousměrné, protisměrné)[editovat | editovat zdroj]
| #vzorků \ směr | sousměrné | protisměrné |
|---|---|---|
| 1 | KMP | BM |
| N | AC | CW |
| ∞ | KA | 2CKAS |
je vhodné znát všechny alg. ale vysvětlit stačí cca první 3
- algoritmy vyhledávání vzorku v textu se liší v závislosti na tom, zda je vzorek předzpracován či nikoliv
- trivialni algoritmus - na kazde pozici zkus porovnat cely vzorek (bez předzpracování vzorku)
- s předzpracováním vzorku – vhodné pro DIS
- pracují jako určitý typ konečného automatu
- dělí se dále dle počtu hledaných vzorků (1, N, nekonečno) a podle směru porovnávání vzorku s textem (sousměrné/protisměrné)
- 💡 text se prochází vždy zleva doprava
Hledání 1 vzorku v textu[editovat | editovat zdroj]
Knuth-Morris-Pratt algoritmus (→ sousměrný)[editovat | editovat zdroj]
- porovnavame postupne vzor a text (od nějakého offsetu)
- prvni neshoda ⇒ posun offsetu o největší postfix shodující se s prefixem (již zkontrolované části)
- pomocné pole P, které říká odkud ve vzorku je možné porovnávat, aby již porovnaná část textu odpovídala vzorku
- 💡 optimalizace trivialniho algoritmu aby se nevracel porad zpet o celou jiz zkontrolovanou cast
- možný preprocess vzoru s odkazy na prefix
- O(m + n) (délka textu + vzorku)
Boyer-Moore algoritmus (← protisměrný)[editovat | editovat zdroj]
- matchuje se od konce vzorku na začátek, vzorek se přikládá zleva doprava
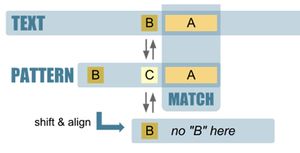
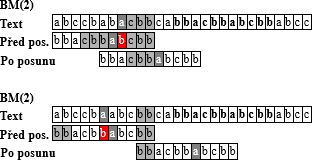
- prvni neshoda ⇒ posun vzorku doprava o SHIFT[pozice_kolize_vzorku, kolizni_znak_textu]
- varianta: Bad-Character SHIFT: když nesedí nějaká pozice, posunu vzorek doprava co nejméně tak, aby na sebe lícoval znak, který způsobil kolizi z textu a znak ve vzorku
- dané 2-rozměrné SHIFT pole
- po "kolizním" posunu vzorku začítám porovnávat znova od konce vzorku
- 💡 funguje dobře na velké abecedy
- varianta: Good-Suffix SHIFT: posun tak, aby se shodovala již kontrolovaná část (kombinace posunu BM a KMP)
- P1[kolizni_znak_textu] - poslední výskyt 'kolizni_znak_textu' ve vzorku (pro znaky co nejsou ve vzoru délka celého vzorku)
- P2[pozice_kolize_vzorku] - ∀zkontrolovanou část (postfix odkonce vzorku) je dán skok na stejný podřetězec vyskytující se dříve ve vzorku.
- délka nejmenšího posun co zarovná postfix (od j dál)
- SHIFT'= max(P1[kolizni_znak_textu],P2[pozice_kolize_vzorku])' je vybrán větší skok z P-polí
- varianta: Bad-Character SHIFT: když nesedí nějaká pozice, posunu vzorek doprava co nejméně tak, aby na sebe lícoval znak, který způsobil kolizi z textu a znak ve vzorku
- O(m*n) ale v praxi O(m/n) (velké abecedy), na běžném textu je mnohem efektivnější než KMP
- 💡 celý algoritmus lze dobře řešit konečným automatem (abeceda – znaky ve vzorku a speciální znak pro všechny ostatní znaky, stavy – pozice ve vzorku)
Hledání N (konečného počtu) vzorků v textu[editovat | editovat zdroj]
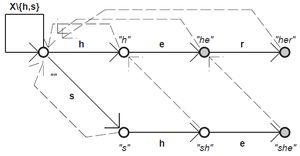
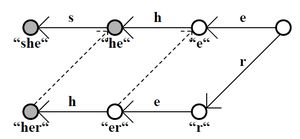
Aho-Corasick (→ sousměrný)[editovat | editovat zdroj]
- předzpracování (konečný automat) + lineární průchod
- stavy – všechny prefixy hledaných vzorků
- postavíme strom dopředných hran podle prefixů
- doplníme zpětné hrany podle postfixů vzorků
- (pro znaky, pro které není def. dopředná funkce určuje zpětná funkce nejdelší vlastní prefix stavu, který se vyskytuje mezi stavy – když to nejde dopředu, vrátí se po zpětné funkci, když to nejde ani tady, vrátí se zase po zpětné funkci)
- 💡 při dojití do přijímacího stavu je třeba zkontrolovat jestli nebylo s tímto slovem přijato i jiné, které by bylo postfixem tohoto (buď pomocí zpětné funkce, anebo definováním množiny přijímaných slov v každém přijímacím stavu)
- časová složitost O(m+Σ(nᵢ))
Commentz-Walter (← protisměrný)[editovat | editovat zdroj]
- kombinace BM a AC, konečný automat jako u AC, ale stavy odpovídající postfixům. Při kolizi složitější posun (tři posouvací funkce, ze dvou se bere maximum a z výsledku a třetí se bere minimum)
- časová složitost O(m*min(n_i))
Hledání ∞ vzorků v textu[editovat | editovat zdroj]
Konečný automat (→ sousměrný)[editovat | editovat zdroj]
- umožňuje definovat přijímaná slova pomocí regulárních výrazů
- nedeterministický KA -> převede se na deterministický KA
Dvoucestný konečný automat se skokem (2CKAS) (← protisměrný)[editovat | editovat zdroj]
- konečný automat, přechází mezi stavy (pozice v hledaném vzorku) a zároveň posouvá (skáče) se vzorkem na prohledávaném textu