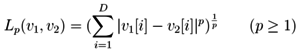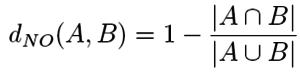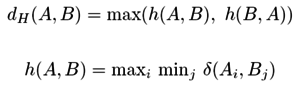Databázové modely a jazyky/MMDB
Z ωικι.matfyz.cz
Obsah
Podobnostní dotazy v multimediálních databázích, metrické indexacní metody. (nové od 2011) (🎓)[editovat | editovat zdroj]
Podobnostní dotazy v multimediálních databázích[editovat | editovat zdroj]
Funkce podobnosti $ δ: U \times U \rightarrow R $ - libovolná fce vracející pro 2 dekriptory z univerza podobnostní skóre
- základní dotazy
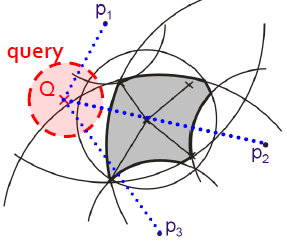
- range - vezme se objekt $ Q $ a poloměr dotazu $ r $
- k-Nearest Neigbour - vybere k nejpodobnějších objektů k dotazu (💡 lze použít i na regresi a klastrování)
- Vstup
-
- trénovací množina klasifikovaných vzoru $ M $
- vzor $ v $, který chceme klasifikovat
- a celé kladné číslo $ k $
- Algoritmus
-
- v množine $ M $ najdeme množinu $ N $ obsahujíci $ k $ vzoru, ktere jsou k vzoru $ v $ nejbližší ze všech vzorů z $ M $
- vzoru $ v $ dáme klasifikaci, která je nejčastejší v množine $ N $
- Reverse kNN - objekt Q a číslo k -> vrátí všechny objekty pro které je Q v kNN
- advanced queries
- Distinct kNN (DkNN) - vrať k nejbližších a disjunktních sousedů
- skyline - vrať prvky z množiny vyhovující nejlépe dvěma/více atributům
- aggregation (top-k operator)
- SQL
- nativní SQL - výhody: nemusí se měnit ex.db, nemá restrikce na range dotazy ; nevýhody: pomalé (nejsou indexy, ani optimalizace dotazů), musí se doprogramovat funkcionalita
- SQL extensions (např. SIREN - rozšiřuje SQL o podobnostní dotazy) - nové db objekty (dat.typy, vzdálenostní fce, indexy), nativní predikáty pro WHERE, operátory - similarity JOIN
Metrické indexování[editovat | editovat zdroj]
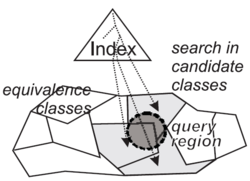
metrický model podobnostního vyhledávání[editovat | editovat zdroj]
místo metrické vzdálenosti se používá levnější spodní odhad (lower-bound)
- pivoti (pro odhad vzdálenosti)
- globální - statické indexy (platné po celý život indexu)
- lokální - dynamické objekty zvolené během indexování (💡 centroidy klusterů)
- vnitřní dimense ρ(S,d) = μ^2/2σ^2 (intrinsic dimensionality)
- statistický ukazatel odvozený z distribuce vzdáleností v databázi
- slouží jako indikátor indexovatelnosti db pod danou metrikou
- vysoká vnitřní dimense - data netvoří shluky a tedy jsou špatně strukturovaná, 💡 prokletí dimese
- nízká - dobře strukturovaná a tvoří těsné shluky
metrické přístupové metody (Metric Access Methods)[editovat | editovat zdroj]
- algoritmy a/nebo datové struktury umožňující rychlé podobnostní hledání v metrickém modelu
- 💡! nepatří k nim R-strom
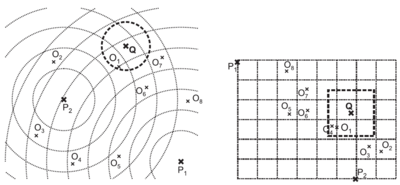
Pivotové tabulky[editovat | editovat zdroj]
- třída indexů používající mapování dat na prostor pivotů
- vzdálenostní matice - vzdálenosti od každého z pivotů
- (L)AESA - (Linear) Approximating and Eliminating Search Algorithm
- AESA - každý prvek je pivot, rychlé hledání sousedů, pomalá kontrukce tabulky
- k prvků jsou pivoti, matice má rozměr O(|S|)
- NN query - cyklus vylepšuje kandidáty
- +spatial access methods
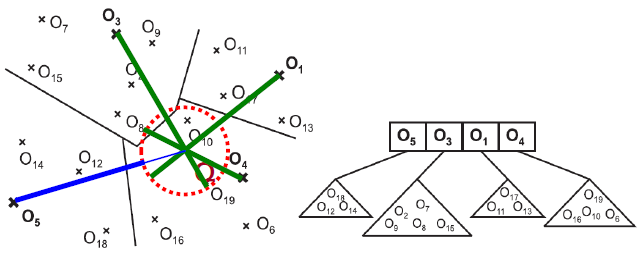
Stromové indexy[editovat | editovat zdroj]
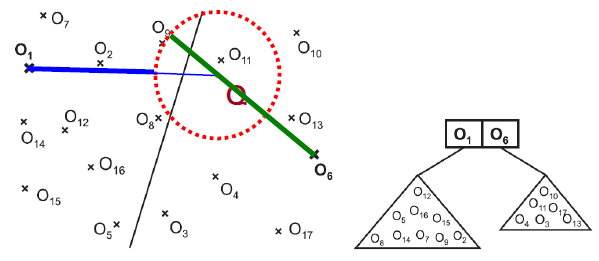
- gh-stromy (Generalized Hyperplane Tree) nadrovinový binární strom (hyperplane = nadrovina)
- konstrukce - vyber 2 pivoty (např nejvzdálenější prvky) a rozděl db na dvě partišny nadrovinou podle vzdáleností, rekurzivně pokračuj
- range query - otestuj na překrytí s query obě partišny, rekurzivně pokračuj níž a testuj stejně
- příklad pro levou partišnu (podstrom)
- pokud nejbližší možný objekt v query (vzhledem k O1) je dále než nejvzdálenější možný objekt v query (vzhledem k O6), pak neprojdeme levý podstrom (pokud spodní odhad z O1 je větší než horní odhad z O6)
- $ δ(Q, O1) - r > δ(Q, O6) + r $
- 💡 tedy můžeme projít i oba podstromy
- GNAT (Geometric Near-neighbor Access Tree) rozšíření na n-pivotů + tabulka vzdáleností
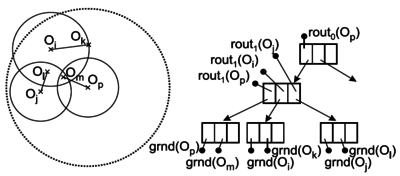
- (P)M-tree - inspirován R-stromem (vyvážený, regiony jsou ale kruhové, data jsou v kořenech (stránky na disku), vnitřní uzly jsou routing entries se středy kruhových regionů a poloměrem)
- využívá hierarchické hnízdění metrických regionů a je vyvážený
Hashed indexes[editovat | editovat zdroj]
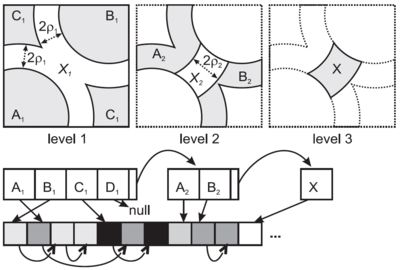
- D-Index
- hashovaný index, základem jsou prstence
- parametr 2ró je tloušťka prstence
- parametr dm je median vzdálenosti od pivotu k jeho objektům
- hashovaci fce bps vrací
- 2 pokud je součástí prstence
- 1 vně prstence (💡 tzn. není v prstenci)
- 0 uvnitř prstence (💡 tzn. není v prstenci)
- ruzne $ bps $ fukce se kombinují do řetězců hash kódu
- pokud hashovací kód obsahuje 2 patří do exkluzní množiny
- rekurzivně se zahashují znovu dokud se exkluzní množiny dostatečně nezmenší
- struktura
- hashované regiony jsou organizované do přihrádek na disku - parametry bps funkce se těžce určují
- přehashování exkluzní množiny definuje další level D-indexu
| další zdroje |
|---|
|