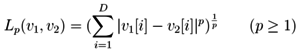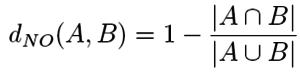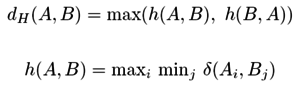Databázové modely a jazyky/Odborne
Obsah
XML data v relacích, indexace XML dat, podobnost XML dat, XML a webové služby. (nové od 2011) (🎓🎓🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
Indexace XML[editovat | editovat zdroj]
Metody indexace
- Indexace úplného textu
- nevýhoda: nelze dotazovat podle struktury
- Indexace relací klasicky (Lore) ???
- Číselná schémata
- indexování založené na pozicích
- použití absolutních resp. relativních adres pro reprezentaci pozic slov a značek v XML dokumentu
- Dietzovo číslování
- ...
- indexování založené na pozicích
- ...
- Absolutní souřadnice regionu (ARC)
- D( S, E )
- D : číslo dokumentu
- S : počátečni pozice, E : koncová pozice v dokumentu
- výhody: pro dotazování
- nevýhody: aktualizace v listu znamená, že všechny následníky je třeba změnit také
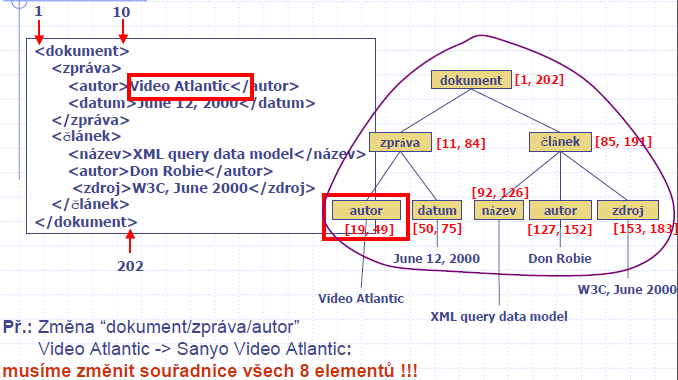
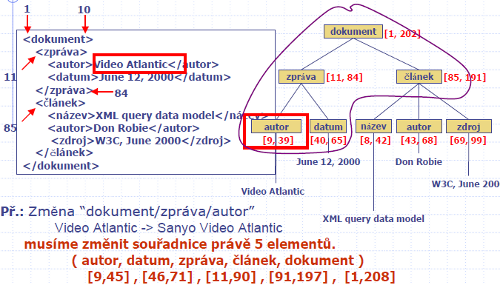
- Relativní souřadnice regionu (RRC)
- RRC uzlu n v XML stromu: [ c1, c2 ]
- c1 : počet byte z počáteční pozice rodičovského uzlu k počáteční pozici n
- c2 : počet byte z počáteční pozice rodičovského uzlu ke koncové pozici uzlu n
- výhoda: aktualizace je menší oproti ARC
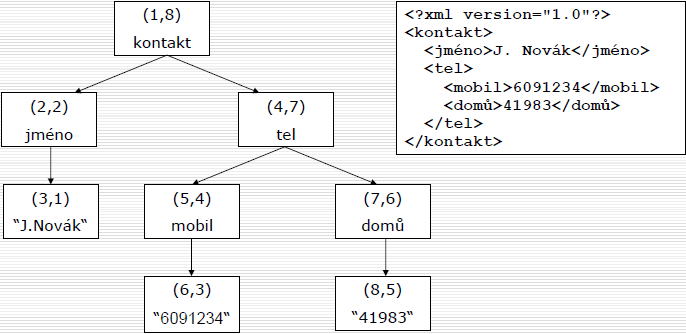
- Dietzovo číslování
- Preorder průchod - potomci každého uzlu následují při preorder průchodu stromem za svým rodičovským uzlem
- Postorder průchod - každý uzel posloupnosti je uveden až za svými potomky
- Konstrukce číselného schématu
- každému uzlu v∈N přiřadíme dvojici (x,y) značící preorder resp. postorder pořadí
- uzel v∈N s ohodnocením L(v) = (x,y) je potomkem uzlu L(u) = (x',y') právě když x' < x & y' > y
Podobnost XML dat[editovat | editovat zdroj]
- Typ dat
- Podobnost dokumentů
- Podobnost schémat
- Podobnost dokumentů a schémat
Podobnost XML dokumentů[editovat | editovat zdroj]
- Idea
- Vstup: Dokumenty D1 a D2
- Výstup: sim(D1, D2) ∈ [0,1]
- Přístupy:
- Zjistíme jak složité je transformovat dokument D1 na D2
- Editační vzdálenost stromů T1 na T2
- Definujeme reprezentaci D1 a D2, která umožní efektivní vyhodnocení podobnosti
- Př. reprezentace množinou cest, reprezentace signálem, …
- Zjistíme jak složité je transformovat dokument D1 na D2
Editační vzdálenost
(pro stromy) minimální počet operací pro transformaci stromu T1 na strom T2
- Editační operace na XML stromech
- Insert - vloží uzel n na pozici danou rodičovským uzlem p a pořadím určujícím pozici v rámci podelementů p
- Delete - smaže listový uzel n
- Relabel - přeznačí uzel n
- InsertTree - vloží celý podstrom T na pozici danou rodičovským uzlem p a pořadím určujícím pozici v rámci podelementů p
- DeleteTree - celý podstrom T s kořenem n je smazán
Minimální editační vzdálenost se jaksi vyhodnocuje pomoci dynamickeho programovani
Tree Alignment
Obdoba editační vzdálenosti
Myšlenka: Pro stromy T1 a T2 vybudujeme tzv. alignment
- Do obou stromů vložíme uzly tak, aby výsledné stromy T1’ a T2’ měly stejnou strukturu (bez ohledu na označení), tj. pokud bychom je přiložili na sebe, překrývaly by se
- Postup
- Vybudujeme alignment
- Každé dvojici překrývajících se uzlů přiřadíme skóre
- Vzdálenost stromů = součet skóre
Obe dve transformace dokumentu jsou NP-tezke (tipl bych si, ze jsou primo slabe NP-tezke)
- Hledání minimální editační vzdálenosti XML stromů je obecně NP-těžký problém
- Tree Alignment: pokud je stupeň stromu omezený, lze minimální vzdálenost nalézt v polynomiálním čase, jinak je to NP-těžký problém.
Reprezentace množinami cest
Myšlenka: XML strom = množina cest
Které cesty budeme brát?
- Všechny různé cesty z kořene do listu
- Všechny různé cesty z kořene do listu a všechny jejich pod-cesty
- Všechny různé cesty z kořene do listu a všechny jejich pod-cesty + informace o četnosti
Problém podobnosti stromů se redukuje na určení velikosti průniku množin cest
Poznámka: Přístup ignoruje uspořádání
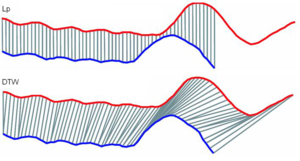
Signál XML dokumentu
Myšlenka: XML dokument reprezentujeme jako signál (impuls = počáteční/koncový tag)
Problém podobnosti XML dokumentů jsme převedli na problém podobnosti signálů
- Postup
- Signály jsou periodicky zopakovány (asi aby byly stejne dlouhe)
- Je na ně aplikována diskrétní Fourierova transformace
- Výsledek je lineárně interpolován
Podobnost XML dokumentů a schémat[editovat | editovat zdroj]
Problém: Chceme porovnat podobnost XML dokumentu D (stromu) a XML schématu S (množina regulárních výrazů)
Možná myšlenka: z dokumentů odvodíme schéma a porovnáme schémata (prozatím se nevyužívá a potřebovali bychom hodně dokumentů)
Existující přístupy:
- Metoda měřící počet elementů, které se vyskytují v D, ale ne v S a naopak
- Metoda, měřící nejkratší vzdálenost mezi D a „všemi“ dokumenty validními vůči S
Podobnost XML schémat[editovat | editovat zdroj]
Problém: podobnost regulární výrazů, resp. gramatik
Typické použití je integrace XML schémat - několik systémů poskytuje stejná (podobná) data v různých formátech → chceme sjednotit do společného schématu (XML Schema, relační, objektové, …)
- Obecná myšlenka
- Definujeme množinu pomocných podobnostních funkcí (matchers), kde každá vyhodnocuje podobnost určité charakteristiky (např. podobnost listů, podobnost jmen kořenových elementů, podobnost kontextu, …)
- Výsledky podobnostních funkcí jsou (váženě) agregovány do výsledné podobnosti
Poznámka: Velké množství metod využívá strojové učení (např. pro nastavení vah, pro vyhodnocování, …)
Algoritmy:
- Cupid - dvě fáze vyhodnocování (lingvistická a strukturální)
- COMA - kombinace velké množiny matcherů s uživatelskou interakcí
Matching velkých schémat
- Problém: U velkých schémat nechceme matchovat každý uzel s každým
- Myšlenka: Dekomponujeme problém do menších a jejich výsledky sloučíme
XML a webové služby[editovat | editovat zdroj]
- http://cs.wikipedia.org/wiki/Webov%C3%A1_slu%C5%BEba
- http://cs.wikipedia.org/wiki/SOAP
- http://cs.wikipedia.org/wiki/Web_Services_Description_Language
Datový model RDF, dotazovací jazyk SPARQL[editovat | editovat zdroj]
RDF[editovat | editovat zdroj]
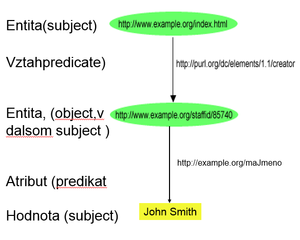
RDF (Resource Description Framework) Dátový model tvorený orientovaným grafom ( bez násobných hrán)- prostředí na popis (webovských) zdrojů. Uložený v XML
Rozlišujeme Zdroj( moze mat vlasnosti), Prázdny uzol a literál ( Dátová hodnota ktorá nie je zdroj , môže mat dátový typ )
RDF graf je možné reprezentovať : Množinou, Graficky, Slovami v abecede, Gramatikom , najčastejšie sa používa zoznam trojíc (subject,predicate,object)
Forma zápisu je N3 notácia, zložitý formalizmus alebo používanejšia Turtle:
- Turtle : URI ( jedinečná identifikácia ) v hranatých zátvorkách , forma prefixovej skratky
- Literály v úvodzovkách
- Trojice uzatvorené bodkou
- Mezery, eol, … se ignorují
- Opakujúce hodnoty môžeme vynechať, oddeľovať nie . ale ;
- Viac trojíc s rovnakým subjekt a predicate oddeľovať objekty ,
- Môžeme redukovať uzly na prázdne uzly , takýto uzol má lokálne meno ale nemá url
Prázdne uzly:
exstaff:85740 exterms:address ??? . ??? exterms:street "1501 Grant Avenue" . ??? exterms:city "Bedford" .
RDF informuje o typoch , tz tvrdenia o tvrdeni
exproducts:triple123 rdf:type rdf:Statement . exproducts:triple123 rdf:subject ex:index.html .
Vyuzitie pri vyhladavacoch, kniznice, eshopy
Zdroje
http://www.ksi.mff.cuni.cz/~pokorny/dj/prezentace/1_34.ppt http://www.w3schools.com/webservices/ws_rdf_example.asp
RDF Schema[editovat | editovat zdroj]
Rožšírenie RDF o triedy pre zdroje, zavedenie dedičnosti( len fw, nedefinuje žiadne triedy)
SPARQL[editovat | editovat zdroj]
Dotazovanie nad RDF datami. Hladaju sa zdroje s istymi vlastnostami . Syntax velmi podobna ako v SQL
SELECT ?(čo)
WHERE { predikat, trojica splnajuca vlastno ?(čo) má vlastnosť. }
Construct: vratia RDF graf tvoreny substituciou za premene
ASK: Vracia true/false ak bol vzor najdeny alebo nie
DESCRIBE : Vracia RDF graf, ktory popisuje najdene zdroje
OPTIONAL : Prida dodatocnu informaciu ale nefailne ked nenajde vhodne.
Data
_:a foaf:name "Alice" . _:a foaf:knows _:b . _:a foaf:knows _:c . _:b foaf:name "Bob" . _:c foaf:name "Clare" . _:c foaf:nick "CT" .
Dotazy
PREFIX foaf: <http://xmlns.com/foaf/0.1/> SELECT ?nameX ?nameY ?nickY WHERE { ?x foaf:knows ?y ; ?x foaf:name ?nameX . ?y foaf:name ?nameY . OPTIONAL { ?y foaf:nick ?nickY } }
Vysledok
| ?nameX | ?nameY | ?nickY |
|---|---|---|
| Alice | Bob | Prazdny vysledok, nieje to null |
| Alice | Clare | CT |
Pekne jednoduche dotazy [1]
Podobnostní dotazy v multimediálních databázích, metrické indexacní metody. (nové od 2011) (🎓)[editovat | editovat zdroj]
Podobnostní dotazy v multimediálních databázích[editovat | editovat zdroj]
Funkce podobnosti $ δ: U \times U \rightarrow R $ - libovolná fce vracející pro 2 dekriptory z univerza podobnostní skóre
- základní dotazy
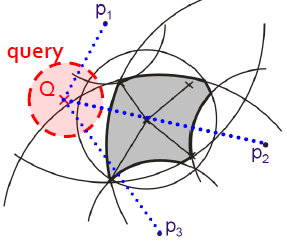
- range - vezme se objekt $ Q $ a poloměr dotazu $ r $
- k-Nearest Neigbour - vybere k nejpodobnějších objektů k dotazu (💡 lze použít i na regresi a klastrování)
- Vstup
-
- trénovací množina klasifikovaných vzoru $ M $
- vzor $ v $, který chceme klasifikovat
- a celé kladné číslo $ k $
- Algoritmus
-
- v množine $ M $ najdeme množinu $ N $ obsahujíci $ k $ vzoru, ktere jsou k vzoru $ v $ nejbližší ze všech vzorů z $ M $
- vzoru $ v $ dáme klasifikaci, která je nejčastejší v množine $ N $
- Reverse kNN - objekt Q a číslo k -> vrátí všechny objekty pro které je Q v kNN
- advanced queries
- Distinct kNN (DkNN) - vrať k nejbližších a disjunktních sousedů
- skyline - vrať prvky z množiny vyhovující nejlépe dvěma/více atributům
- aggregation (top-k operator)
- SQL
- nativní SQL - výhody: nemusí se měnit ex.db, nemá restrikce na range dotazy ; nevýhody: pomalé (nejsou indexy, ani optimalizace dotazů), musí se doprogramovat funkcionalita
- SQL extensions (např. SIREN - rozšiřuje SQL o podobnostní dotazy) - nové db objekty (dat.typy, vzdálenostní fce, indexy), nativní predikáty pro WHERE, operátory - similarity JOIN
Metrické indexování[editovat | editovat zdroj]
metrický model podobnostního vyhledávání[editovat | editovat zdroj]
místo metrické vzdálenosti se používá levnější spodní odhad (lower-bound)
- pivoti (pro odhad vzdálenosti)
- globální - statické indexy (platné po celý život indexu)
- lokální - dynamické objekty zvolené během indexování (💡 centroidy klusterů)
- vnitřní dimense ρ(S,d) = μ^2/2σ^2 (intrinsic dimensionality)
- statistický ukazatel odvozený z distribuce vzdáleností v databázi
- slouží jako indikátor indexovatelnosti db pod danou metrikou
- vysoká vnitřní dimense - data netvoří shluky a tedy jsou špatně strukturovaná, 💡 prokletí dimese
- nízká - dobře strukturovaná a tvoří těsné shluky
metrické přístupové metody (Metric Access Methods)[editovat | editovat zdroj]
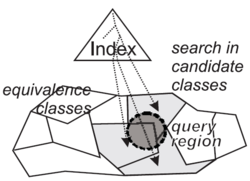
- algoritmy a/nebo datové struktury umožňující rychlé podobnostní hledání v metrickém modelu
- 💡! nepatří k nim R-strom
Pivotové tabulky[editovat | editovat zdroj]
- třída indexů používající mapování dat na prostor pivotů
- vzdálenostní matice - vzdálenosti od každého z pivotů
- (L)AESA - (Linear) Approximating and Eliminating Search Algorithm
- AESA - každý prvek je pivot, rychlé hledání sousedů, pomalá kontrukce tabulky
- k prvků jsou pivoti, matice má rozměr O(|S|)
- NN query - cyklus vylepšuje kandidáty
- +spatial access methods
Stromové indexy[editovat | editovat zdroj]
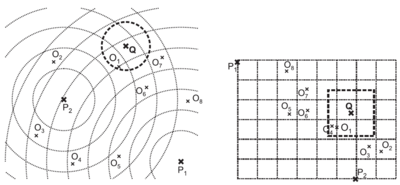
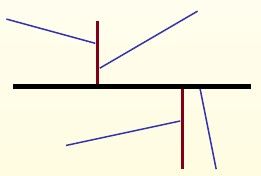
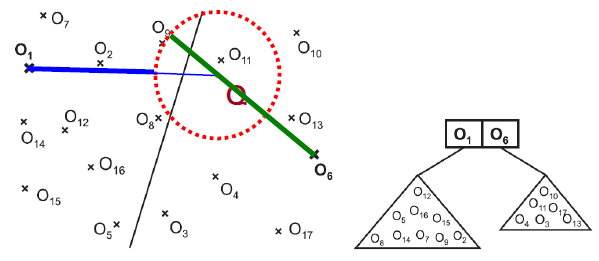
- gh-stromy (Generalized Hyperplane Tree) nadrovinový binární strom (hyperplane = nadrovina)
- konstrukce - vyber 2 pivoty (např nejvzdálenější prvky) a rozděl db na dvě partišny nadrovinou podle vzdáleností, rekurzivně pokračuj
- range query - otestuj na překrytí s query obě partišny, rekurzivně pokračuj níž a testuj stejně
- příklad pro levou partišnu (podstrom)
- pokud nejbližší možný objekt v query (vzhledem k O1) je dále než nejvzdálenější možný objekt v query (vzhledem k O6), pak neprojdeme levý podstrom (pokud spodní odhad z O1 je větší než horní odhad z O6)
- $ δ(Q, O1) - r > δ(Q, O6) + r $
- 💡 tedy můžeme projít i oba podstromy
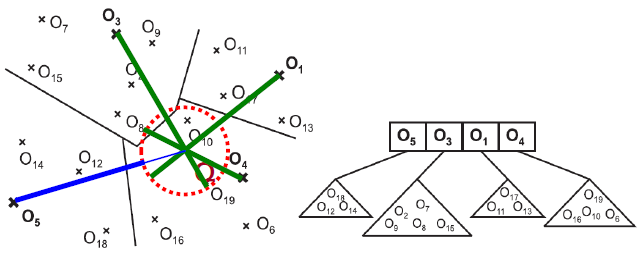
- GNAT (Geometric Near-neighbor Access Tree) rozšíření na n-pivotů + tabulka vzdáleností
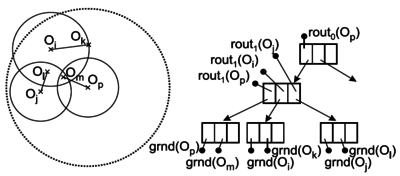
- (P)M-tree - inspirován R-stromem (vyvážený, regiony jsou ale kruhové, data jsou v kořenech (stránky na disku), vnitřní uzly jsou routing entries se středy kruhových regionů a poloměrem)
- využívá hierarchické hnízdění metrických regionů a je vyvážený
Hashed indexes[editovat | editovat zdroj]
- D-Index
- hashovaný index, základem jsou prstence
- parametr 2ró je tloušťka prstence
- parametr dm je median vzdálenosti od pivotu k jeho objektům
- hashovaci fce bps vrací
- 2 pokud je součástí prstence
- 1 vně prstence (💡 tzn. není v prstenci)
- 0 uvnitř prstence (💡 tzn. není v prstenci)
- ruzne $ bps $ fukce se kombinují do řetězců hash kódu
- pokud hashovací kód obsahuje 2 patří do exkluzní množiny
- rekurzivně se zahashují znovu dokud se exkluzní množiny dostatečně nezmenší
- struktura
- hashované regiony jsou organizované do přihrádek na disku - parametry bps funkce se těžce určují
- přehashování exkluzní množiny definuje další level D-indexu
| další zdroje |
|---|
|