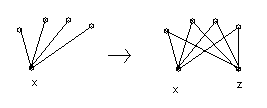Složitost I
| Složitost I | ||||
|
- Oficiálne materiály KTIML on-line
-
Učebné texty k Složitosti a NP úplnosti - obsahujú dôkazy k vetám z prednášky(nefunkční odkaz) -
Materiály z mff.modry.cz - Další poznámky (sxw)
- Studnice: Complexity.pdf (velmi detailni studentska skripta!)
- Nějaké kusy jsou asi i ve státnicovém okruhu Složitost
Obsah
Zápočtové príklady[editovat | editovat zdroj]
Takto vypadajú niektoré riešenia niektorých zápočtových príkladov, preberaných na cvičeniach. Zatial aspoň tých ťažších. Ospravedlňujem sa za gramatycké i iné prípadné chyby. Dúfam, že to niekomu raz pomôže. jsimlo 14:30, 27 Jan 2006 (CET)
Nebo řešení (alespoň náznakem a bez záruky) všech je v materilech na "modrym" viz "resene priklady by jirja" --Jirja 13:48, 3 Feb 2006 (CET)
Cvičení 3[editovat | editovat zdroj]
Stok[editovat | editovat zdroj]
1. Nechť je orientovaný graf $ G = (V,E) $, kde $ |V| = n $, zadán maticí sousednosti. Navrhněte algoritmus, který zjistí, zda $ G $ obsahuje stok, tj. vrchol $ x $ takový, že vstupní stupeň $ x $ je $ n-1 $ a výstupní stupeň $ x $ je $ 0 $, přičemž algoritmus smí použít (přečíst) pouze $ O(n) $ prvků matice (předpokládejme, že před zahájením algoritmu je již celá matice načtena do paměti).
Takový vrchol má ve svém sloupci samé $ 1 $ (kromě svého řádku) a ve svém řádku samé $ 0 $ a navíc je v grafu určitě jen jeden. Proto mohu jít od bodu po řádku $ [0,0] $ a dokud nalézám nuly, pokračovat (tím vylučuji všechny vrcholy, příslušné sloupcům, kde by musela být $ 1 $).
Když najdu jedničku, pokračuji po sloupcích a vylučuji vrcholy příslušné řádkům. Pokud na řádku nebo sloupci $ k $ vylezu z matice, pak $ k $ je jediný kandidát na stok a mohu otestovat jeho celý řádek nebo sloupec.
Bipartita[editovat | editovat zdroj]
2. Navrhněte algoritmus založený na BFS (breadth-first search), který rozhodne, zda daný neorientovaný graf je bipartitní a pokud ano, oddělí obě partity.
Začneme z nějakého vrcholu, obarvíme ho barvou $ A $ a potom v BFS pokud jdeme z vrcholu s barvou $ A $, obarvíme všechny jeho následníky barvou $ B $ a naopak. Pokud bychom zjistili, že nějaký z následníků už je barevný stejně jako jeho předch. vrchol, víme, že graf není bipartitní (do vrcholu existuje cesta ze zdroje, jak sudé, tak liché délky) a končíme.
Topologické číslování[editovat | editovat zdroj]
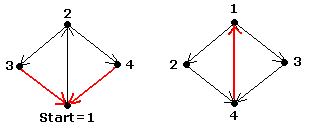
3. Víme, že DFS (depth-first search) nalezne topologické očíslování vrcholů acyklického grafu podle klesajících časů opuštění. Dokažte nebo vyvraťte, že pro libovolný (i cyklický) graf takové očíslování minimalizuje počet inkonzistentních hran (tj. takových, které vedou proti topologickému očíslování).
Neplatí. Protipříklad:
Inkonzistentní hrany jsou označeny červeně. První očíslování vypadlo z DFS, druhé je minimální (co do počtu inkonzistentních hran).
Polosouvislost[editovat | editovat zdroj]
4. Orientovaný graf $ G $ se nazývá polosouvislý, pokud pro každé dva vrcholy $ x,y $ existuje v $ G $ buď orientovaná cesta z $ x $ do $ y $, nebo orientovaná cesta z $ y $ do $ x $. Navrhněte algoritmus na testování polosouvislosti grafů s co nejlepší asymptotickou složitostí
- Pro acyklické:
Platí věta Acyklický graf $ G $ je polosouvislý, právě když v něm existuje orientovaná cesta na všech vrcholech. -- implikace zprava doleva je trivka, zleva doprava jde sporem (v topologickém uspořádání najdu $ (i,i+1)\notin E $.
- Pro obecné:
Algoritmus:
- Najít silně souvislé komponenty (lin. algoritmus)
- Sestavit acyklickou kondenzaci (jedna SSK --> 1 vrchol)
- Pustit na to acyklický případ
Platí totiž věta: G je polouvislý, právě když jeho acyklická kondenzace je polosouvislá. --- implikace zprava doleva je triviální, vezmu dvě komponenty, mezi nimi je cesta jedním směrem, a v rámci těch komponent to jde převést na cestu z kteréhokoliv do kteréhokoliv vrcholu. Druhá implikace je ještě lehčí -- najdu cestu a zkondenzuji.
Cvičení 4[editovat | editovat zdroj]
Dijkstra Error[editovat | editovat zdroj]
Zkonstruujte příklad grafu se zápornými hodnotami hran (bez záp. cyklů), na kterém selže Dijkstrův algoritmus.
4 vrcholy A, B, C, D a hrany/váhy AB: 3, BC: -3, AC: 1, CD: 1. Při hledání cesty z A mu vyjde, že D je ve vzdálenosti 2 (cesta ACD), když ve skutečnosti je vzdálenost 1 (cesta ABCD, nejlepší je si to nakreslit).
Nespolehlivá síť[editovat | editovat zdroj]
Máme nějakou komunikační síť, tedy orientovaný $ G=(V,E) $, kde pro každou hranu $ (u,v) $ je dána "spolehlivost" $ 0<w(u,v)<1 $ (pravděpodobnost, že tato hrana při komunikaci neselže). Tyto pravděpodobnosti jsou nezávislé. Vytvořte algoritmus pro nalezení nejspolehlivější cesty v síti.
- řešení: Dijkstra upravený tak, že $ \infty := 0 $, $ 0 := 1 $, $ + := * $, extractMin := extractMax a decreaseKey := increaseKey
- řešení:$ w'(e)= -\log_2 w(e) $ a normální Dijkstra
Dijkstra s omezenou váhovou funkcí[editovat | editovat zdroj]
Nechť je dán vážený orientovaný graf $ G=(V,E) $, kde $ |V|=n, |E|=m $ a váhy na hranách jsou zadány funkcí $ w:E\to \{1,2,\dots,k\} $. Dále předpokládejme, že $ k<n $. Implementujte Dijkstrův algoritmus tak, aby běžel v $ O(nk+m) $
Vytvořím pole délky $ k\cdot n $ a v něm udržuji vrcholy v aktuální vzdálenosti od začátku (vrcholy se stejnou vzdáleností ve spojácích). Potom při extractMin stačí jít o $ k $ prvků dopředu, protože jinak je všechno v nekonečnu. Při decreaseKey jen přehodím jeden prvek. Z toho mám:
- extractMin $ O(k) $
- decreaseKey $ O(1) $
Celkem tedy $ O(nk+m) $. Dá se to i vylepšit a používat jen pole délky $ (k+1) $ (za pomoci modulení).
Vylepšení[editovat | editovat zdroj]
Změňte implementaci předchozího problému tak, aby algoritmus běžel v $ O((n+m)\log k) $.
Vyrobím si haldu (o velikosti maximálně $ k+1 $), ze které vedou pointery na podle vzdálenosti setříděné spojáky vrcholů se stejnou vzdáleností $ \mod k+1 $. Potom:
- extractMin -- max. mi zanikne jeden spoják a musím upravit haldu -- $ O(\log k) $
- decreaseKey -- max. $ O(\log k) $ na odebrání prvku ze vzdálenější pozice + $ O(\log k) $ na přidání do bližší.
Cvičení 5[editovat | editovat zdroj]
Ja som na tom cviku nebol, ale príklady sú očividne v pohode. Prvý je trivka, druhý používa trochu z výrokovej a predikátovej logiky. Asi je rozumné vedieť, čo je to CNF a DNF, inak žiadne zákernosti. jsimlo 16:00, 27 Jan 2006 (CET)
SAT[editovat | editovat zdroj]
- Nechť máme k dispozici černou skřínku, která umí řešit SAT (rozhodovací problém splnitelnosti CNF formulí) v polynomiálním čase. Zkonstruujte algoritmus, které pro danou CNF najde v polynomiálním čase splňující ohodnocení proměnných, pokud takové ohodnocení existuje.
Algoritmus bude fungovat po krokoch. V kazdom kroku i dosadi za $ x_i $ hodnotu, BUNO napriklad hodnotu 0. Formulu s dosadenou hodnotou predlozi SAT skrinke a podla odpovedi bud necha $ x_i $ = 0, alebo dosadi hodnotu opacnu.
Po najviac n krokoch, kde n je pocet premennych formule, dosadime za vsetky $ x_i $ nejake hodnoty, ktore stale splnuju formulu. Mame teda nejake jej splnitelne ohodnotenie, pokial existuje.
Pozn.: Algoritmus predkladal upravenu formulu SAT skrinke iba raz za kazdy krok. Mohlo sa nam preto stat, ze vysledok, ktory sme vygenerovali nie je spravnym vysledkom, pretoze ziaden spravny vysledok neexistuje (hlavne u nesplnitelnych formuli :). To sa da osetrit jednoducho. Uplne na zaciatku algoritmu sa spytame SAT skrinky, ci je vstupna formula vobec splnitelna. Pokial nie, nema vyznam ulohu dalej riesit. Pokial splnitelna je, urcite najdeme jej ohodnotenie.
Zlozitost: (n+1)-krat pouzijeme polynomialnu skrinku SAT, sme teda stale polynomialny.
TAUT[editovat | editovat zdroj]
- Definujme problém TAUT následovně:
- Instance: Boolovská formule F sestávající z n proměnných a operací negace, disjunkce a konjunkce.
- Otázka: Je F tautologie?
- a) Je TAUT ve třídě NP?
- b) Je TAUT ve třídě co-NP?
- c) Jaká je složitost TAUT pokud je F CNF?
- d) Jaká je složitost TAUT pokud je F DNF?
Třída co-NP je třída takových problémů, jejichž "otočené" verze (odpovědi NE a ANO se prohodí) jsou v NP (jestli $ P \subsetneq coNP \cap NP $, nikdo neví)
- a) Nevie sa (víme, že je to ve třídě co-NP, ale o NP nic netušíme)
- b) Ano. Certifikatom pre zápornú odpoveď je ohodnotenie, kde formula nie je splnitelna.
- c) Linearna.
- $ A \land B $ je tautologia, pokial aj A aj B su tautologie. Kazda podformula formule F, plna samych disjunkci, teda musi byt sama o sebe tautologiou. A to je prave vtedy, ked sa v nej nachadza nejaka formula a zaroven i jej negacia.
- d) coNP-C. Ukazeme, ze pokial vieme riesit coTAUT, vieme riesit i SAT.
- $ SAT \propto \overline{TAUT} $
- Majme problem $ \overline{TAUT} $. Instance: Formule F je DNF. Otazka: $ \exists x_1..x_n: F[x] = 0? $
- A majme problem $ SAT\,\! $. Instance: Formule F je CNF. Otazka: $ \exists x_1..x_n: F[x] = 1? $
- Trivialne vieme, ze $ (F[x] = 1) \equiv (\lnot F[x] = 0) $ a pomocou DeMorganovych pravidiel vieme, ze $ \lnot CNF[x] \equiv DNF[\lnot x] $.
- Takze $ \overline{TAUT}[\lnot F] \equiv SAT[F] $. $ \overline{TAUT} $ je teda NP-C a TAUT je coNP-C.
Cvičení 6[editovat | editovat zdroj]
Snažil som sa problémy opísať čo najpolopatistickejšie, dúfam, že i korektne, keď tak ma opravte. Keď tomu človek vôbec nerozumie, mal by si asi skúsiť prečítať aspoň definíciu NP a NP-úplnosti z teórie ešte pred zápočtom. Doporučujem texty od Majerecha, je to tam celkom príjemne napísané. Rovnako pomôže, keď človek vie, o čom sú tie problémy, na ktoré sa snažíme prevádzať. To sa dá pomerne stručne a jasne nájsť napríklad na slajdoch od Čepka. Inak potom je to už jednoduché. Žiadne extra drsné triky ani nápady.. :)) jsimlo 15:56, 27 Jan 2006 (CET)
LOUP[editovat | editovat zdroj]
- Definujme problém LOUP (loupežníci) následovně:
- Instance: Přirozená čísla a1, ... , an
- Otázka: Existuje podmnožina T množiny indexů S = {1, ... ,n} taková, že $ \sum_{i \in T} a_i = \sum_{i \in S-T} a_i $
- Dokažte, že LOUP je NP-úplný problém.
- $ LOUP \in NP $:
- Certifikat: Mnozina indexov rozdelenia.
- $ SP \propto LOUP $:
- Mame zadanie SP ako mnoziny $ a_1..a_n,\ b $.
- Polozime $ A = \sum_{i=1}^n a_i, \qquad b' = \max {\{b, A-b\}} \ge A/2, \qquad a_{n+1} = 2b' - A $ a riesime LOUP pre $ a_1,\ ...,\ a_n,\ a_{n+1} $.
- Inymi slovami, mame kopu roznych minci $ a_1 .. a_n $ a chceme z nich poskladat sumu b algoritmom delenia na polovicu. Vyrobili sme si preto jednu specialnu mincu $ a_{n+1} $, ktora dolpna celkovy sucet minci tak, aby pri ich rozdeleni na dve polovice bolo b na jednej strane a zvysne mince na druhej. Nasa specialna minca skonci podla velkosti b bud na jednej strane spolu z b alebo na druhej strane spolu s ostatnymi mincami. Tak ci tak sme oddelili b od zvysku.
- Tvrdenie: Skonstruovana instancia pre LOUP ma riesenie, prave ked ma riesenie vstupna instancia SP.
- $ \Rightarrow $
- $ \exists T \subseteq {1..n+1}: \sum_{i \in T} a_i = \sum_{i \in S-T} a_i $
- BUNO nech $ n+1 \notin T $, potom $ \sum_{i=1}^{n+1} a_i = A+2b'-A = 2b' $, a teda $ \sum_{i \in T} a_i = b' $, pretoze nam LOUP rozdelil zadanie na dve polovice.
- Takze pokial
- a) $ b' = b $, potom T je riesenim SP,
- b) $ b' = A-b $, potom S-T je riesenim SP.
- Takze pokial
- $ \Leftarrow $
- $ T: \sum_{i \in T} a_i = b $
- Takze pokial
- a) $ b' = b $, potom priradme $ T':= T $,
- b) $ b' = A-b $, potom priradme $ T':= S-T $.
- Plati, ze $ \sum_{i \in T'} a_i = b' $ a preto nase $ T'\,\! $ je riesenim LOUP.
PATH[editovat | editovat zdroj]
- Nejkratší cestu mezi dvěma vrcholy v neorientovaném váženém grafu lze nalézt pomocí Dijkstrova algoritmu, pokud jsou zadané váhy na hranách nezáporné. Jak se změní složitost této úlohy, pokud povolíme, aby byly váhy záporné?
Zlozitost bude NP-úplná. Ukazeme, ze $ HK \propto HC $ a $ HC \propto PATH $. PATH je nas problem zo zadania, HK je problém hamiltonovské kružnice, HC je problém hamiltonovské cesty.
$ PATH \in NP $
- Certifikat: zoznam vrcholov cesty.
$ HK \propto HC $
- Mam neorientovany graf G a chcem v nom najst HK (hamiltonovská kružnice). Zvolim si nejaky vrchol x z grafu G. Potom upravim graf G tak, ze pridam novy vrchol z a spojim ho hranou zo vsetkymi vrcholmi, ktore boli spojene z x. Takze mam $ \forall y: e(x,y) \equiv e(z,y) $.
- V upravenom grafe hladam HC (hamiltonovská cesta) z vrcholu x do vrcholu z. Pokial najdem, tak posledna hrana v najdenej ceste vedie z vrcholu v do z. Takyto vrchol v je ale spojeny hranou aj z vrcholom x, a preto sa da posledna hrana $ e(v,z) $ nahradit za $ e(v,x) $, cim uzavrieme kruznicu prechadzajucu vsetkymi povodnymi vrcholmi. Nasli sme teda HK pomocou HC.
$ HC \propto PATH $
- Mam graf G a chcem v nom najst HC (hamiltonovská cesta). Pridam ku grafu G ohodnotenie -1 na vsetkych hranach. Na takto ohodnotenom grafe pustim nas problem PATH, ktory mi najde najkratsie cesty. V pripade nasho ohodnotenia bude ale najkratsia cesta zaroven i cesta, ktora prejde najviac vrcholov. Overime teda, ci ma hladana cesta dlzku $ -(n-1) $ a pokial ano, je tato cesta HC.
0-1 CP[editovat | editovat zdroj]
- Definujme problém 0-1 CP (celočíselné programování) následovně:
- Instance: Celočíselná matice A řádu m krát n a celočíselný vektor b délky m
- Otázka: Existuje vektor x délky n obsahující pouze čísla 0 a 1 takový, že $ Ax \le b $ ?
- Dokažte, že 0-1 CP je NP-úplný problém.
$ CP \in NP $
Certifikat: Vektor $ x $ (zlozeny z nul a jedniciek).
$ SP \propto CP $
Mame zadanie problemu SP: cisla $ a_1..a_n $ a cislo $ b $.
Z cisel $ a_1..a_n $ poskladame maticu a vektor nasledujucim sposobom:
$ A' = \begin{pmatrix} a_1 & a_2 & \cdots & a_n \\ a_1 & a_2 & \cdots & a_n \\ \vdots & \vdots & \ddots & \vdots \\ -a_1 & -a_2 & \cdots & -a_n \end{pmatrix} ,\qquad b' = \begin{pmatrix} b \\ b \\ \vdots \\ -b \end{pmatrix} $
Myslím, že stačí: $ A' = \begin{pmatrix} a_1 & a_2 & \cdots & a_n \\ -a_1 & -a_2 & \cdots & -a_n \end{pmatrix} ,\qquad b' = \begin{pmatrix} b \\ -b \end{pmatrix} $
Na takto postavenu maticu $ A' $ a vektor $ b' $ pustime nas problem CP. Pokial CP uspeje, tak najde vektor $ x $ pre ktory bude platit: $ A'x \le b' $.
Z toho vieme, ze $ (\vec a * \vec x \le b) \land (- \vec a * \vec x \le -b) $ a preto $ \vec a * \vec x = b $.
Pozn. 1: Z nerovnosti sme si trivialnou fintou spravili rovnost.
Pozn. 2: Riadkovy vektor $ \vec a $ krat stlpcovy vektor $ \vec x $ je cislo $ b $ (resp. vektor $ \vec b $ o velkosti 1x1).
Rovnost $ \vec a * \vec x = b $ nam ale hovori, ze vektor $ \vec x $ zlozeny z nul a jedniciek nam vlastne vybera z mnoziny vsetkych $ a_i $ take prvky, aby spolu davali sucet $ b $. Ostava nam teda uz iba vektor $ x $ previest na mnozinu indexov, ktora bude riesenim problemu SP.
Ine riesenie.
$ CP \in NP $
Certifikat: Vektor x (zlozeny z nul a jedniciek).
$ SAT \propto CP $
Necht mame instanci SAT v CNF $ F=(x_1 \lor \neg x_2 \lor x_4) \land (\neg x_1 \lor x_3 \lor \neg x_4) \land (\neg x_2 \lor \neg x_3) $ a necht mame BB resici 0-1CP. Potom instanci 0-1CP zkonstrujme nasledovne
$ \begin{cases} x_1+(1-x_2)+x_4 \ge 1\\ (1-x_1)+x_3+(1-x_4) \ge 1\\ (1-x_2)+(1-x_3) \ge 1 \end{cases} \rightarrow \begin{cases} -x_1+x_2-x_4 \le 0\\ x_1-x_3+x_4 \le 1\\ x_2+x_3 \le 1 \end{cases} $
IP[editovat | editovat zdroj]
- Definujme problém IP (izomorfismus podgrafů) následovně:
- Instance: Neorientované grafy G a H
- Otázka: Je graf G izomorfní s nějakým podgrafem grafu H? (varianta 1)
- Otázka: Je graf G izomorfní s nějakým indukovaným podgrafem grafu H? (varianta 2)
- Dokažte, že obě varianty IP jsou NP-úplné problémy.
$ IP \in NP $
Certifikat: zoznam dvojic vrcholov, ktore sa maju na seba zobrazit.
$ KLIKA \propto IP $
Mam graf H a chcem v nom najst kliku o velkosti k. Nech viem riesit problem IP. Zostrojim si graf G ako uplny graf na k vrcholoch, $ G = K_k $, a hladam pomocou IP graf G v grafe H. Pokial ho najdem, tak som nasiel kliku velkosti k v grafe H a teda som vyriesil problem KLIKA. Toto funguje pre obe varianty, pretoze klika je maximalny podgraf. Maximalny podgraf bude urcite indukovany, pokial bude existovat.
Blackbox pro SP[editovat | editovat zdroj]
Zadání: Nechť máme k dispozici „černou skřínku“, která umí řešit rozhodovací verzi problému součtu podmnožiny v polynomiálním čase. Skřínka odpovídá pouze ANO-NE. Zkonstruujte algoritmus, který pro daný vstup optimalizační verze problému součtu podmnožiny najde v polynomiálním čase (vzhledem k délce binárního zápisu vstupních dat) optimální řešení.
- Máme black box, který funguje takto:
$ BB(a_1,\ ..., \ a_n, \ b) = \begin{cases} true - pokud\quad \exists\ T \subseteq \{1,...,n\}:\quad \sum_{i \in T} a_i = b\\ false - jinak \end{cases} $
- Chceme algoritmus pro optimalizační verzi - naším cílem je tedy něco takového:
vstup: čísla $ a_1,\ ...,\ a_n $ a nějaký práh b
výstup: množina indexů $ T \subseteq \{1,\ ...,\ n\} $ pro kterou platí:
(definujme: $ sum_T = \sum_{i \in T} a_i $)
- $ sum_T \leq b $
- $ \forall T^'\subseteq \{1,\ ...,\ n\} \wedge T^' \neq T:\ sum_{T^{'}} \leq sum_{T} $
Postup:
Pokud neexistuje přesný součet b, něco tam chybí. Hledáme množinu prvků s minimálním součtem, pro kterou platí, že když ji přidáme k té původní, black box vrátí true.
Hledáme ji tak, ze k původní množině přidáváme postupně mocniny dvojky (1,2,4,8 atd.) ze kterých se dá chybějící hodnota poskládat.
Až blackbox vrátí true, máme rozšíření původní množiny o mocniny dvojky.
Najdeme množinu indexů R ($ sum_R = b $). Potom z R odebereme všechny indexy, které indexují přidané prvky a dostaneme přesně množinu indexů T o kterou nám jde.
!!! Pozor u tohoto algoritmu na to, jak naleznete množinu indexů R.
Napřiklad pro vstup: {3,10}, b=7, popsaným postupem přidáte 1,2,4, blackbox vrátí true a množina indexů R může být třeba {1,2,4}. Pak z ní odeberete přidané prvky a zůstane prázdná množina, co jste asi nechtěli, jelikož optimálním řešením je {3}.
Lepší je algoritmus popsaný ve studnici v PrepisCviceni/Cviceni.pdf
Zkoušení[editovat | editovat zdroj]
Doc. Čepek dává tento rok (2009/10) na zkoušce dva příklady. Pro připuštění ke zkoušce je potřeba mít aspoň jeden (případné nesrovnalosti se doťuknou před zkouškou, ale není to časté). Jeden příklad špatně znamená snížení o stupeň (tj. v úvahu pak připadá rozsah známek 2-4 :)
Na ústní mu záleží na důkazech, třeba větu o separátoru bez jejího důkazu nepovažuje za zodpovězenou. (Člověka se pak zeptá jinou otázku.) Např. u matroidů ho zajímá algoritmus pro hledání optimální množiny, nebo spíš jeho správnost (konkrétně - pokud ji chce člověk dokazovat indukcí - ten indukční krok, viz "Lemma 3: existence optimální podstruktury"). Ale i napsaný algoritmus a definice považuje za "něco". Po případné třetí otázce se ukáže, jestli to je bod dolů, nebo dva.