| (k-páskový deterministický) TS je 5-tice: M = (Q, ∑, δ, q0, F)
|
- Q je konečná množina stavů (řídící jednotky)
- ∑ je konečná pásková abeceda
- obsahuje znak λ pro prázdné políčko
- $ δ : Q \times ∑^k -> Q \times ∑^k \times \{R, N, L\}^k ∪ \{⊥\} $ je přechodová fce
- ⊥ je nedefinovaný přechod
- q0 ∈ Q je počáteční stav
- F ⊆ Q je množina přijímajících stavů.
💡 Pozn: UTS umí simulovat libovolný jiný TS M nad libovolným vstupem w.
|
Algoritmicky nerozhodnutelné problémy (halting problem) (9×🎓)
| Zážitky ze zkoušek
|
- Algoritmicky nerozhodnutelné problémy, halting problem (2015, Kučera, ke konci i Majerech) - prolítnul můj důkaz LHALT a chtěl dokázat problem: "ekvivalence 2 TS" je RSJ nebo RJ? jsem se s tím v životě nesetkal, tak jsem jenom něco málo odvodil z definice a vlastností m-převoditelnosti, ale asi to na vyhazov nebylo
- Halting problém (2013, Kolman) - Tu som zadefinoval TS, spomenul som kódovanie TS (nič konkrétne iba že to je číslo), Postovu vetu a dokázal som, že L HALT nie je rekurzivný, na záver som spomenul, že to isté sa dá urobiť aj cez množiny. Žiadne doplnkové otázky.
- Algoritmicky nerozhodnutelné problémy (2012, A.Kučera) - Napsal jsem Halting problém + ten jednoduchý důkaz. Dále jsem napsal Riceovu větu a jak souvisí s halting problémem. Nakonec jsem napsal Postův korespondenční problém. To zkoušejícímu stačilo a nebyly žádné další otázky.
- Nerozhodnutelné problémy (2012, Kucera) - Halting problem - jak se dokazuje, Postuv problem, rozhodnuti zdali dana funkce vycisluje dany program
- Algoritmicky nerozhodnutelne problemy (2012, Dvorak) - Zacal sem Church-Turingovou tezi a pojem algoritmus vztahl k TS. Pak sem zadefinoval Rekurzivne spocetne a rekurzivni jazyky. Halting problem, Diagonalni jazyk, Univerzalni jazyk, Postova veta. Pak sem presel od TS k CRF tady sem jako priklad uvedl K a K0, definoval CRF a ORF + intuitivni srovnani s TS U vetsiny veci sem mel i dukazy ( vycislitelnosti sem se bal nejvic z okruhu takze sem to mel celkem nadrceny ). Pak se dvorak ptal jak zjistim ze nejakekj problem je nerozhodnutelny ( aniz by clovek musel furt vymyslet specialni dukazy ) to sem chvili vahal ale pak sem si vzpomel na prevoditelnost Rekurzivnich a rekurzivne spocetnych mnozin pomoci prevodni fce ktera musi byt ORF coz se ukazalo jako spravna odpoved. Posledni sada otazek uz smerovala k tomu co se bude dit kdyz budu mit TS s orakulem, jestli potom budou vsechny problemy budou rozhodnutelne...tady sem nevedel, odpovidal sem hodne diplomaticky ( spravna odpoved je TS s 1 orakulem umi resit nejaky problemy, TS s 2 orakulama umi resit jeste vic problemu atd...ale nikdy nelze pokryt vsechny jazyky ) Jeste dodam ze tohle nakonec Dvorak okomentoval slovy ze je to spis takova zajimavost, nic zasadniho pro statnice.
- Algoritmicky nerozhodnutelné problémy (2012) - Napsal jsem Halting problém + ten jednoduchý důkaz. Dále jsem napsal Riceovu větu a jak souvisí s halting problémem. Nakonec jsem napsal Postův korespondenční problém. To zkoušejícímu stačilo a nebyly žádné další otázky.
- Algoritmicky nerozhodnutelné problémy (2011, Kucera) - Způsob zkoušení: Zdá se, že mu jde o témata, které mají praktický dopad (např. halting problem). Ptal se, jestli znám ještě další nerozhodnutelný problém. Dostali jsme se i k Riceově větě, ale bránil mi ji dokazovat, protože to nebylo v otázce. Známku mi neříkal. S Majerechem zkoušeli někoho společně. Uklidňovali ho, že mu chtějí pomoct.
- Algoritmicky nerozhodnutelné problémy (2010) - Co to je rozh. problém, halting problém, že to souvisí s tím, že množina K není rekurzivní, Riceova věta s důkazem.
- Alg. nerozhodnutelne problemy (2010, P. Kucera) - klasika, definice co to je problem, rozdil mezi rekurzivne spocetnym a rekurzivnim, Churchova teze a ekvivalence s TS, dale halting problem + ten snadny dukaz, Riceho veta a jeste jeden dva dalsi problemy jako zajimavost.
- Nerozhodnutelne problemy (2009, Mlcek) - Halting a Riceova s dokazom, ostatne len nazov
|
instance problému - vstup
rozhodovací problém(odpověď typu ano/ne) - jazyk řetězců popisujících pozitivní instance a otázku, zda dané slovo – instance problému – patří do tohoto jazyka (kladná instance daného problému)
Jazyk $ L $ je rekurzivní (také rozhodnutelný), pokud ∃ TS $ M $, který se vždy zastaví a $ L = L(M) $.
Věta ( problém zastavení
): LHALT = {e;x | Mₑ(x)↓} je RSJ, ale není RJ
Dk (sporem přes UTS HALT zdroj):
Sporem nechť máme TS HALT(e;x) rozhodující, zda se TS Mₑ zastaví nad daty x (a TS HALT se zastaví vždy a vydá buď 0 nebo 1).
Potom lze vyrobit TS PODRAZₚ(x)↓ ⇔ HALT(x;x)↓ = 0 ( tj. pokud HALT(x;x)↓ = 1 tak se PODRAZₚ(x) uměle zacyklí - tedy můžeme ho vytvořit úpravou TS HALT ).
PODRAZₚ má Gödelovo číslo p. Pak ale:
- HALT(p;p)↓ = 1 $ \stackrel{\text{z def.HALT}}{⇔} $ PODRAZₚ(p)↓ $ \stackrel{\text{z def.PODRAZ}}{⇔} $HALT(p;p)↓ = 0
a to je spor.
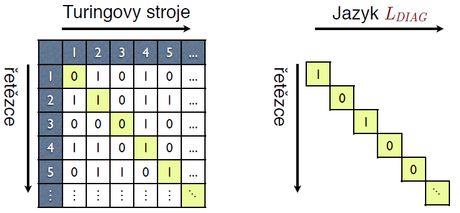
Věta ( diagonalizační jazyk
): LDIAG = {wᵢ ∈ {0, 1}* | wᵢ ∉ L(Mᵢ) } není RSJ (tedy ani RJ)
| Dk (sporem)
|
- Předpokládáme že $ L_{DIAG} $ je RSJ ⇒ ∃ TS M že $ L_{DIAG} = L(M_e) $ z čekož nám vychází ale spor:
- $ w_e \in L(M_e) ⇔ w_e ∈ L_{DIAG} ⇔ w_e \notin L(M_e) $, kde první ekvivalence vyplývá z toho, že $ L_{DIAG} = L(M_e) $ a druhá ekvivalence z definice $ L_{DIAG} $
|
Věta ( univerzální jazyk
): Lᵤ = L(U) (kde U je UTS) je RSJ, ale není RJ
| Dk (sporem)
|
- To, že $ L_u $ je RSJ jsme ukázali tím, že jsme popsali UTS, který jej přijímá.
- Zbývá tedy ukázat, že není rekurzivní. Z Postovy věty stačí dokázat pouze, že $ \overline L_u $ není RSJ.
- Sporem nechť $ \overline L_u = L(M) $. Pomocí stroje $ M $ zkonstruujeme stroj $ M’ $, který bude přijímat diagonalizační jazyk $ L_{DIAG} $. Už víme, že $ L_{DIAG} $ není RSJ a dospějeme tím tedy ke sporu.
- $ M’ $ dostane na vstupu slovo $ w $ a má rozhodnout, zda $ w ∈ L_{DIAG} $, tedy jestli stroj s kódem $ w $ odmítne slovo $ w $.
- $ M’ $ udělá pouze to, že zkontroluje, zda w kóduje Turingův stroj způsobem, jaký jsme popsali při popisu UTS. Pokud $ w $ nekóduje syntakticky správně TS, odpovídá prázdnému TS, který slovo $ w $ určitě nepřijme a $ M’ $ tedy skončí přijetím. V opačném případě připíše $ M’ $ za $ w $ kód $ 111 $ (kód „;“) a za ně okopíruje opět slovo $ w $. Poté $ M’ $ spustí na tomto slově stroj $ M $, pokud $ M $ přijme, přijme i $ M’ $, pokud se $ M $ zastaví a odmítne, odmítne i $ M’ $, pokud se $ M $ nezastaví, nezastaví se ani $ M’ $.
- $ M’ $ ale přijímá jazyk $ L_{DIAG} $, protože $ M’(w) $ přijme ⇔ $ w $ je validním kódem TS $ N $ a $ N(w) $ nepřijme, což je ekvivalentní tomu, že $ U(w;w) $ nepřijme a $ M(w; w) $ přijme. Fakt, že $ L(M’) = L_{DIAG} $, je však ve sporu s tím, že $ L_{DIAG} $ není RSJ.
|
| další problém: Postův korespondenční problém
|
- Vstup
-
dva konečné seznamy $ \alpha_{1}, \ldots, \alpha_{N} $ and $ \beta_{1}, \ldots, \beta_{N} $ slov nad abecedou $ A $ z alepoň 2 symbolů.
- Řešení
sekvence indexů $ (i_k)_{1 \le k \le K} $ kde $ K \ge 1 $ a $ 1 \le i_k \le N $ pro všechna $ k $, že:
- $ \alpha_{i_1} \ldots \alpha_{i_K} = \beta_{i_1} \ldots \beta_{i_K}. $
- Problém
Zda existuje řešení.
|
Státnice -- Softwarové systémy
Složitost a vyčíslitelnost -- Tvorba algoritmů (10🎓), NP-úplnost (15🎓), Aproximační algoritmy (6🎓), Vyčíslitelné funkce a rekurzivní množiny (8🎓), Nerozhodnutelné problémy (9🎓), Věty o rekurzi (6🎓)
Datové struktury -- Stromy (32🎓), Hašování (13🎓), Třídění (10🎓)
Databázové systémy -- Formální základy: Relace (12🎓), Datalog (9🎓), Ostatní (0🎓) Modely a jazyky: SQL (7🎓), DIS (7🎓), Odborné (3) Implementace: Transakce (5🎓), Indexace (10🎓), Komprese (3)
Softwarové inženýrství -- Programovací jazyky a překladače, Objektově orientované a komponentové systémy, Analýza a návrh softwarových systémů
Systémové architektury -- Operační systémy, Distribuované systémy, Architektura počítačů a sítí
Počítačová grafika -- Geometrické modelování a výpočetní geometrie, Analýza a zpracování obrazu, počítačové vidění a robotika, 2D počítačová grafika, komprese obrazu a videa, Realistická syntéza obrazu, virtuální realita
🎓 - znamená kolikrát byla otázka u státnic