| (k-páskový deterministický) TS je 5-tice: M = (Q, ∑, δ, q0, F)
|
- Q je konečná množina stavů (řídící jednotky)
- ∑ je konečná pásková abeceda
- obsahuje znak λ pro prázdné políčko
- $ δ : Q \times ∑^k -> Q \times ∑^k \times \{R, N, L\}^k ∪ \{⊥\} $ je přechodová fce
- ⊥ je nedefinovaný přechod
- q0 ∈ Q je počáteční stav
- F ⊆ Q je množina přijímajících stavů.
|
| Zážitky ze zkoušek
|
- Np-úplnost (2014, konzultace) - definice: třídy NP, polynom.převoditelnost, NP-těžký, NP-úplný, zmínit P =? NP, Cook-Levinova věta + důkaz
- NP-úplné problémy (2014) - Definoval jsem nedeterministický Turingův stroj, třídu NTIME, NP-úplnost a dokázal převod obecného NTS počítajícího nějaký NP problém na KACHL (Cook-Levinova věta). Na závěr jsem zmínil, že ještě existují další NP-úplné problémy např. SAT, Batoh, Obchodní cestující atd. Žádné další převody jsem nespecifikoval. Tato odpověď byla přijata bez jediné otázky.
- Cook-Levinova veta (2012, Koubek) - definoval jsem NP, NPC, atd., dokazal vetu kachlikovanim. Pak se me ptal co znamena pojem uplnosti obecne a naky jeho zneni nebo dusledek Cook-Levinovy vety (neco jako ze kdyz bych umel polynomialne resit NPC problem, tak uz vsechny NP problemy jdou resit polynomialne). Pak chtel co je PSPACE uplnost a nakej priklad (obecna booleovska formule). SAT ve zneni s KNF se mu uplne nelibil, prej se vetsinou definuje obecne. Kdyz mu prisedici Majerech rikal, ze jak jsem ho definoval se to u nas vetsinou dela, tak se Koubek mracil :)
- NP-Uplne problemy (2012) - Definoval jsem jazyk, problem, NP, prevody, NP-uplnost a strucne predvedl dukaz cook levina. Zkousejiciho opet neznam, ptal se jen na to jake dalsi NP-uplne problemy, jinak byl spokojen.
- Úplné problémy pro třídu NP, Cook-Levinova věta (2012, Čepek/Koubek/Dvořák) - Člověk by řekl, že jednoduchá otázka, ale kurevsky mi zatopila, neb jsem nebyl schopen dát do kupy přesnou definici NP a převoditelnosti pomocí TS (a Čepek 5 minut před tím jednoho kolegu vyhodil, neb neznal definici). Naštěstí mě několikrát nakopli a tak jsme nakonec došli k tomu, co to teda je NP-úplný problém. C-L větu + důkaz převodem na kachlíkování jsem uměl, což Čepka evidetně potěšilo, takže nakonec v pohodě.
- NP, NP-úplnost, příklady (2012, Král) - Trochu jsem se zamotal do toho, jestli je třeba, aby se NTS zastavil po polynomiálním počtu kroků (v první chvíli jsem myslel, že ne a že když to bude třeba, tak že NTS = DTS, ale to je blbost - třeba to sice není, ale pokud tak tu definici dáme, tak se nic nezmění). Byl hodný.
- NP-uplnost, Cook-Levinova veta (2011, Kucera) - definice NP, prevoditelnost, NPC, prevod na kachlikovani a na SAT
- NP-uplnost (2011, Loebl) - Zacal som definiciou Turingovho stoja a postupne som definoval vsetko az po NP-uplnost, dokazal kachlikovani, prave ked som pisal prevod KACHL->SAT tak prisiel skusajuci, pozrel sa na to vsetko a povedal ze to staci.
- Úplné problémy pro třídu NP + Cook Levinova věta. (2010, Hladík) - Definice (od TS až k NPÚ), Důkaz Cook Levinovy věty (KACHL + převod na SAT), vyjmenovat problémy co byly na přednášce (zadání, otázka), ukázat převod SAT na KLIKA.
- NP-úplnost (2009, Matoušek) - Přesná formální definice - rozhodovací problém, jazyk problému, NTS pro rozhodovací problém, složitost výpočtu NTS, NP. Převoditelnost aritmetických funkcí, problémů, NP-těžkost, NP-úplnost. Příklady problémů. Vztahy P, NP, NPC (obrázek s podmnožinami, je NPC doplněk k P v NP?). Alternativní definice NP přes ověřování řešení. Jak popsat NP, NPC laikovi.
|
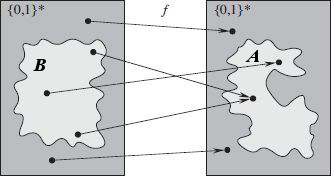
Ilustrace polynomiálního převodu/redukce z jazyka B na jazyk A pomocí redukční fce f. Pro vstup x ∈ {0,1}* má otázka zda x ∈ B stejnou odpověď jako otázka zda x ∈ A. 💡 myslím že je vidět proč se mu říká někdy redukce(btw f NENÍ prostá)
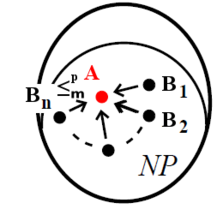
NP-těžkost ⇐ ∀ jazyk B ∈ NP: B$ ≤^p_m $A
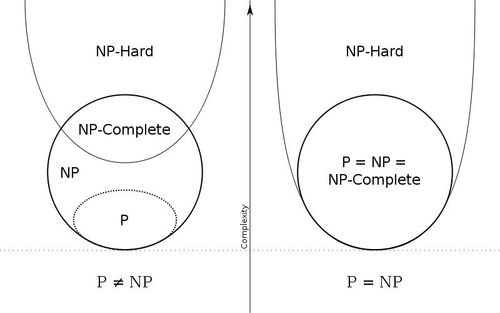
Eulerův diagram pro P, NP, NPC a NP-těžké množiny problémů. Levá strana platí pro P ≠ NP (předpokládá se), a pravá pro P = NP (až na prázdný jazyk a jeho doplněk nejsou nikdy NPC)
- odpověď typu ano/ne - rozhodovací problém (jestli vstup patří do binární relace L ⊆ {0, 1}*)
- vstup - instance problému
- úloha - pro daný vstup x nalézt y co splňuje požadovanou vlastnost ( jestli oba patří do binární relace R ⊆ {0, 1}* × {0, 1}* )
Třídy polynomiálních jazyků, relací:
- $ P= \bigcup_{i\in \mathbb N}DTIME(n^i) $ - problémy rozhodnutelné v polynomiálním čase
- $ PSPACE=\bigcup_{i\in\mathbb N}DSPACE(n^i) $ - problémy rozhodnutelné v polynomiálním prostoru
Třída polynomiálně ověřitelných problémů $ NP $ (nedeterministicky polynomiální)
Problém A je ve třídě NP, právě když existuje polynomiální NTS M, který řeší A.
- 💡 Na rozdíl od deterministického případu netrváme na tom, že výpočet musí skončit i pro nepřijímané instance.
- 💡 NTS $ M=(Q, \Sigma, \delta, q_0, F) $, kde $ \delta:Q\times\Sigma\mapsto\cal P(Q\times\Sigma\times\{R, N, L\}) $.
- obdobně jako DTS, ale místo přechodové funkce je zde zobrazení do množiny možných pokračování
- alternativní def. pomocí certifikátů
L ∈ NP ⇐ ∃ polynomiální algoritmus (daný jazykem B), že polynomiálně dlouhý certifikát y dosvědčuje fakt x ∈ L
- 💡 Je opět nutné uvažovat pouze polynomiálně dlouhé certifikáty, neboť složitost ověřování se měří vzhledem k délce x i certifikátu y
- 💡 obecně platí P ⊆ NP, protože pokud umíme problém řešit polynomiálně nepotřebujeme certifikát
Polynomiální převoditelnost, úplnost a jejich vlastnosti.[editovat | editovat zdroj]
B $ ≤^p_m $A (jazyk B polynomiálně převoditelný/redukovatelný na A ) pokud ∃ f: {0,1}*→{0, 1}* spočitatelná v polynomiálním čase a platí: x ∈ B ⇔ f(x) ∈ A
Jazyk A ∈ NP-hard (NP-těžký) ⇐ ∀ jazyk B ∈ NP : B $ ≤^p_m $A
Jazyk A ∈ NPC (NP-Complete, NP-úplný) ⇐ A ∈ NP ∧ A ∈ NP-hard
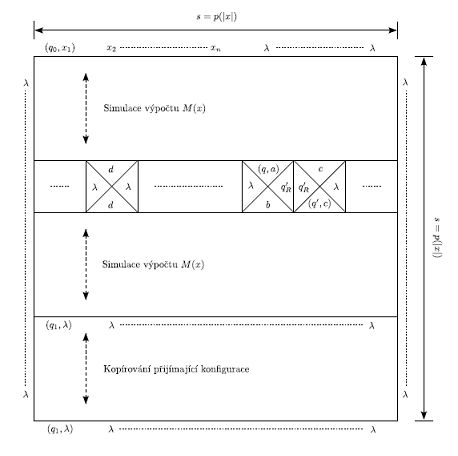
Přehled převodu obecného problému A ∈ NP na problém KACHL. Horní hrana čtvercové sítě je obarvena počáteční konfigurací, spodní hrana přijímající konfigurací, boky jsou obarveny symbolem λ. Pro ukázku je zde řádek kachlíků s provedením instrukce (q’, b, R) ∈ δ(q, a), dva kachlíky slouží k provedení instrukce, na ostatních místech je jen kopírovací kachlík pro okopírování barev na další řádek. Po ukončení výpočtu je dokopírována přijímající konfigurace až ke spodní hraně čtvercové sítě.
∀ symbol a ∈ ∑ nejprve přidáme typ kachlíku,
barvy jsou z množiny:
ABECEDA ∪ (STAVY × ABECEDA) ∪ {qL, qR | q ∈ STAVY}
(💡 tj.speciální barva pro posun vlevo/vpravo)
Kachlíkování (KACHL, anglicky Tiling)
- Instance: Množina barev B, přirozené číslo s, čtvercová síť S velikosti s x s, hrany jejíchž krajních políček jsou obarveny barvami z B. Dále je součástí instance množina K⊆BxBxBxB s typy kachlíků, které odpovídají čtverci, jehož hrany jsou obarveny barvami z B. Tyto kachlíky mají přesně definovaný horní, dolní, levý i pravý okraj a není možné je otáčet.
- Otázka: Existuje přípustné vykachlíkování čtvercové sítě S kachlíky z množiny K? Přípustné vykachlíkování je takové přiřazení typů kachklíků jednotlivým polím čtvercové sítě S, v němž kachlíky, které spolu sousedí mají touž barvu na vzájemně dotýkajících se hranách a kachlíky, které se dotýkají strany S, mají shodnou barvu s okrajem. Jednotlivé typy kachlíků lze použít víckrát.
Věta ( Cook-Levin
): KACHL je NP-úplný problém.
- Dk(KACHL ∈ NP ⇐ jde verifikovat v polynomiálním čase)
KACHL ∈ NP plyne z toho, že dostaneme-li vykachlíkování sítě S, tedy přiřazení typů kachlíků jednotlivým políčkům, dokážeme ověřit v polynomiálním čase, jde-li o přípustné vykachlíkování.
- Dk(KACHL ∈ NPC $ \stackrel{\text{je i NP}}{\Leftarrow} $KACHL ∈ NP-hard ⇐ ∀A∈ NP $ ≤_m^p $KACHL ⇐ ∀NTS v p(n) → KACHL)
Kachl je NP těžký
- Vezměme libovolný problém A ∈ NP, pak jeho NTS M řeší, jestli x ∈ L(M) (zda řetězec x patří do jazyka L(M), neboli zda jeho NTS přijme daný vstup x) v polynomiálním čase polynomu p(n)
- Zkonstruujeme síť p(n) × p(n), zkonstruujeme vhodné kachličky (5 druhů) a obarvení (barvy jsou z množiny ABECEDA ∪ (STAVY × ABECEDA) ∪ {qL, qR | q ∈ STAVY}) tak, aby
- ∀krok výpočtu NTS kódoval jeden vykachličkovaný řádek, 1-2 kachlíky slouží k provedení instrukce, zbytek kopírovací kachličky
- nemusí skoncit po přesně p(n) krocích, takže se doplní kopírováním posledního řádku
- spodní okraj vstupní paska, obarvení výstupniho okraje je výstupní paska
Máme převod libovolného problému A ∈ NP na Kachlíkování a protože KACHL ∈ NP ⇒ KACHL ∈ NPC.
| Dk (detailně ze poznámek):
|
To, že A ∈ NP znamená, že existuje NTS M, který přijímá A (tj. A = L(M)) a počet kroků každého přijímajícího výpočtu je omezen polynomem p(n), BÚNO můžeme předpokládat, že p(n) ≥ n, v opačném případě by M nepřečetl ani celý svůj vstup a pokud by platilo, že p(n) ≤ n, stačí vzít max(p(n), n) místo p(n). Připomeňme si, že podle definice x ∈ A, právě když existuje přijímající výpočet NTS M nad vstupem x, který má délku nejvýš p(|x|). Nechť M = (Q, Σ, δ, q₀, F ), kde Q obsahuje stavy q₀ a qf a {0, 1, λ} ⊆ Σ. Abychom si zjednodušili situaci, budeme BÚNO předpokládat, že M splňuje následující předpoklady (ke každému NTS M₁ lze zkonstruovat NTS M₂, který přijímá týž jazyk jako M₁', „dělá totéž“ a splňuje uvedené podmínky):
- F = {qf }, tj. M má jediný přijímající stav qf různý od q₀.
- Pro každé a ∈ Σ je δ(qf, a) = ∅, tj. z přijímajícího stavu neexistuje definovaný přechod.
- V počáteční konfiguraci hlava stojí na nejlevějším symbolu vstupního slova x, které je zapsáno počínaje od levého okraje vymezeného prostoru délky p(|x|). Zbytek pásky je prázdný.
- Během výpočtu se hlava M nepohne nalevo od místa, kde byla v počáteční konfiguraci.
- Přijímající konfigurace je daná jednoznačně a vypadá tak, že páska je prázdná a hlava stojí na nejlevější pozici vymezeného prostoru. To odpovídá tomu, že než se M rozhodne přijmout, smaže nejprve obsah pásky a přesune hlavu k levému okraji vymezeného prostoru.
Nechť x je instance problému A, popíšeme, jak z M, polynomu p a instance x vytvořit instanci KACHL, pro kterou bude platit, že v ní existuje přípustné vykachlíkování, právě když existuje přijímající výpočet M(x), tj. M(x) přijme. Idea důkazu je taková, že hrany barev mezi dvěma řádky kachlíků budou kódovat konfigurace výpočtu NTS M nad vstupem x. Vhodným výběrem kachlíků zabezpečíme, že v přípustném vykachlíkování bude řada kachlíků simulovat změnu konfigurace na následující pomocí přechodové funkce. Položíme tedy B = Σ ∪ (Q × Σ) ∪ {qL, qR | q ∈ Q}. Zatímco vstupní abecedou stroje M je jen {0, 1, λ}, neboť x musí být binární řetězec, pracovní abecedu stroje M nijak neomezujeme, a proto zde používáme obecnou abecedu Σ, přičemž předpokládáme, že λ ∈ Σ.
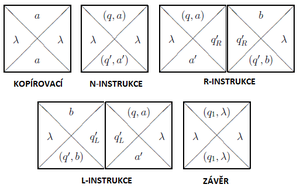 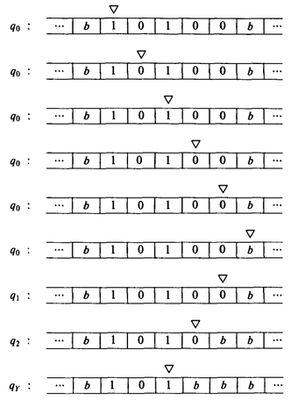 $ \stackrel{odpovídá}{\Rightarrow} $ $ \stackrel{odpovídá}{\Rightarrow} $ 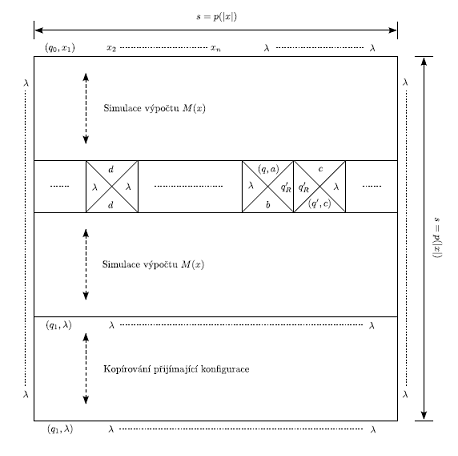
Přehled převodu obecného problému A ∈ NP na problém KACHL. Horní hrana čtvercové sítě je obarvena počáteční konfigurací, spodní hrana přijímající konfigurací, boky jsou obarveny symbolem λ. Pro ukázku je zde řádek kachlíků s provedením instrukce (q’, b, R) ∈ δ(q, a), dva kachlíky slouží k provedení instrukce, na ostatních místech je jen kopírovací kachlík pro okopírování barev na další řádek. Po ukončení výpočtu je dokopírována přijímající konfigurace až ke spodní hraně čtvercové sítě.
|
Pseudopolynomiální algoritmy, silná NP-úplnost (6×🎓)[editovat | editovat zdroj]
| omezení max čísla v instanci polynomem její délky
|
|
$ \large max(I) ≤ p(len(I)) $
nejdůležitější vzorec
(číselné problémy, silná/slabá NPC,...)
|
| Zážitky ze zkoušek
|
- Pseudopolynomiální algoritmy, silná NP-úplnost (2014, konzultace) - Pseudopolynomiální algoritmy definice + příklad, silná NP-úplnost definice + příklad (a souvislosti s apx.schématy)
- Pseudopoly. alg., silná NP-úplnost (2014, Kučera) - Definice len, max, číselnosti, NP-úplnosti, pseudopoly alg., silné NP-úplnosti (napsal jsem bez kvantifikátorů a tedy jsem je musel doplnit). Příklad silně NP-úplného (obchodní cestující) a slabě (součet podmnožiny, loupežníci). Pak padl dotaz k čemu je možné pseudopoly alg. využít - základ pro aproximační schémata.
- Pseudopolynamialni algoritmy a silna NP uplnost (2012, Kucera P.) - Definice obojiho, jedna veticka o tom, ze silne NP-uplne nemaji pseudopol. alg., strucne napsany pseudopol. problem pro batoh, veta o tom, ze pokud bychom nasli pro silne NP-uplny problem pseudopolynamialni alg., muselo by platit, ze P=NP. Nic dalsiho nebylo potreba vedet.
- Pseudopolynomiální algoritmy, silná NP-úplnost (2010, Petr Gregor) - Docela v pohodě, stačilo mu pár definic a příkladů + rozumět tomu. Zkoušející příjemný, popovídání v pohodě. Známka 1.
- Silna NP uplnost (2010, Fiala) - definice a premysleni nad timto tematem, vztah k aproximacnim algoritmum
- pseudopolynomialni algoritmy (2010, Kucera) - formalni definice pseudopolynomialniho algoritmu, silne NPU problem. Algoritmus reseni SP. Priklad silne NPU (TSP s omezenim na vaze hran) a proc je silne NPU (prevod na HK). Nekolik otazek jak souvisi pseudopolynomialni algoritmy a aproximacni algoritmy.
- Pseudopolynomiální algoritmy a aproximační schémata (2008, Trpělivý teoretik) - Napsal jsem špatnou definici pseudopolynomiálních algoritmů, aproximací, AS, a ÚPAS. Na dotaz jestli znám nějaké AS jsem zmínil ÚPAS pro SP, a to že patrně obsahuje nějakou proceduru co cosi prořezává. Posléze se mi podařilo přijít na správnou definici pseudopolynomiálních algoritmů, a to jak by zhruba měl vypadat pseudopolynomiální algoritmus pro problém batohu. Tou dobou ale už všichni ze zkoušky odešli tak mě nechal jít :-)
|
Číselný problém je rozhodovací problém A, pokud ∄ polynom p že ∀ instanci I (problému A) max(I) ≤ p(len(I))
- len(I) - délka binárního zakódování instance I
- max(I) - hodnota největšího zadaného čísla v instanci I (je obsaženo ve vstupu) (NE délka jeho binárního zápisu!)
- 💡 Pro Batoh je len(I) = O(n log₂(B + V)) , ale max(I) = max({B} ∪ {v[1..n]} ∪ {s[1..n]}). Například LOUP nebo Batoh jsou tedy číselné problémy, zatímco SAT nebo KLIKA číselné problémy nejsou.
Pseudopolynomiální algroritmus - pokud je jeho časová složitost omezená polynomem dvou proměnných max(I) a len(I)
- 💡 Alg. pro Batoh je pseudopolynomiální (viz níže). Je-li problém A řešitelný pseudopolynomiálním algoritmem a není-li A číselný problém, pak je zřejmě tento pseudopolynomiální algoritmus ve skutečnosti polynomiální. Pokud bychom tedy pro nějaký nečíselný NP-úplný problém (např. kliku nebo SAT) našli pseudopolynomiální algoritmus, znamenalo by to, že P = NP.
- 💡 pseudopoly alg. lze využít jako základ pro aproximační schémata
NP-úplný problém, pro který ∃ pseudopolynomiální alg., nazýváme slabě NP-úplný.
NP-úplný problém, pro který ∄ pseudopolynomiální alg., nazýváme silně NP-úplný (💡 pokud P ≠ NP).
- 💡 tj. ne každý číselný problém je řešitelný pseudopolynomiálním algoritmem
- 💡 silně NP-úplný problém je NPC i po omezení max čísla v instanci, tj. max(I) ≤ p(len(I))
| formální definice
|
$ p $ je polynom a $ A $ NP-úplný problém:
- $ A(p) $ je restrikce (podproblém) problému $ A $ na instance $ I $ s $ max(I) ≤ p(len(I)) $.
- Silně NP-úplný je problém $ A $, pokud ∃ polynom $ p $, pro nějž je problém $ A(p) $ NP-úplný.
- Slabě NP-úplný je problém $ A $, pokud ∄ polynom $ p $, pro nejž je problém $ A(p) $ NP-úplný.
|
Věta ( OC je silně NP-úplný
): Problém Obchodního cestujícího je silně NP-úplný.
| Dk:
|
- 💡je to číselný problém: $ max(I) $ je v tomto případě největší vzdálenost mezi městy (vzdálenosti nejsou omezené)
- v grafu ex. Hamiltonovská kružnice ⇔ OC obejde všechny města a vzdálenost mezi městy je vždy 1 (nebo alespon omezená)
- ⇒ OC(1) je stále NP-úplný ⇒ OC je silně NP-úplný
|
| buď prvek přidám nebo ne
|
|
$ S[i, sumSoFar] = S[i − 1, sumSoFar] ∨ S[i − 1, sumSoFar − w_i] $
|
Pseudopolynomiální alg. pro (slabě NP-úplný) problém ∃součtu podmnožiny[editovat | editovat zdroj]
💡 Ke státnicim doporučuji spíš ukázat problém ∃součtu podmnožiny, protože je jednodušší než Kučerův Batoh
| hloupý O(2n) rekurzivní algoritmus
|
isSubsetSum([w1,..,wn], sum, i=1, sumSoFar=0)
1 // Base Cases
2 if (sumSoFar == sum) return true
3 if (i == n) return false
4 /* check if sum can be obtained by any of the following
5 (a) excluding the last element
6 (b) including the last element */
7 return isSubsetSum([w1,..,wn], sum, i+1, sumSoFar) ∨ isSubsetSum([w1,..,wn], sum, i+1, sumSoFar + wi)
|

plníme pole zleva nahoru (bottom-up)
- chytrý O(n*sum) algoritmus (bottom-up dynamické programování)
isSubsetSum([w1,..,wn], sum)
1 S[0..n, 0..sum] = False jen S[0, 0] = True (mimo hranice pole také False)
2 for i ← 1..n do
3 for sumSoFar ← 0..sum do
4 S[i, sumSoFar] = S[i − 1, sumSoFar] ∨ S[i − 1, sumSoFar − wi]
5 return S[n, sum]
| Pseudopolynomiální alg. $ Batoh(s, v, B) $ pro (slabě NP-úplný) problém Batohu
|
 0/1 knapsack problem (💡 0/1 = buď předmět vezmu nebo ne) - Vstup : Velikost batohu B, pole 0 < s[1..n] ≤ B velikostí předmětů a pole v[1..n] cen předmětů.
- Výstup : Množina M předmětů, jejichž souhrnná velikost nepřesahuje B (maximalizujeme cenu).
- Prerekvizity : V je suma cen všech předmětů
- Nechť T je tabulka (n + 1) × (V + 1) , na pozici T[j, c] , bude podmnožina indexů prvků celkové ceny přesně c s minimální velikostí.
- Nechť S je tabulka (n + 1) × (V + 1) , na pozici S[j, c] je celková velikost předmětů v množině T[j, c]. Pokud neexistuje množina s předměty ceny přesně c, je na pozici S[j, c] číslo B + 1
- 💡 prakticky 1 tabulka s dvěma vrstvami
- Algoritmus je ze dvou vnořených cyklů, postupně zkouší každý předmět pro ten postupně zvyšuje cenový limit
- tím postupně vytváří zvětšující se množiny prvku (a do 2.tabulky si poznamená jejich celkovou velikost)
- MINImalizuje celkovou velikost předmětů (při zachování celkové ceny)
- výsledek bude v posledním řádku T na poli kde má S největší povolenou velikost
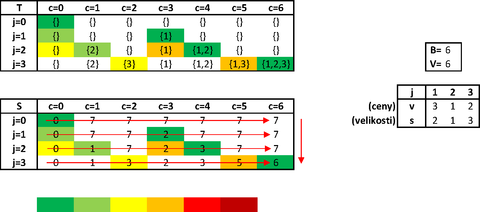 běh alg. Batoh(s, v, B), barvy ukazují jak vznikaly množiny (pokud se jen nekopírovaly z minulého kroku cyklu přes předměty), šipky ukazují směr průchodu alg. tabulkou (bottom-up) Batoh(s, v, B):
0: # Inicializace tabulek:
1: for (c = 0 to V) {
2: T[0, c] = ∅; # temp
3: S[0, c] = B + 1; # sums of sizes
4: }
5: S[0, 0] = 0;
6: # Cyklus přes všechny předměty:
7: for (j = 1 to n) {
8: T[j, 0] = ∅;
9: S[j, 0] = 0;
10: # Cyklus zvyšující cenový limit:
11: for (c = 1 to V)
12: if (v[j] ≤ c) && # zda předmět j může být součástí řešení
13: (S[j – 1, c] > S[j - 1, c - v[j]] + s[j]) { # minimalizujeme celkovou velikost předmětů při zachování c
14: S[j, c] = S[j – 1, c − v[j]] + s[j];
15: T[j, c] = T[j – 1, c − v[j]] ∪ {j};
16: } else {
17: S[j, c] = S[j – 1, c];
18: T[j, c] = T[j – 1, c];
19: }
20: }
21: c = max{c | S[n, c] ≤ B};
22: return T[n, c];
💡 bottom-up dynamické programování
💡 Kučerova verze algoritmu MINImalizuje celkovou velikost předmětů (při zachování celkové ceny), běžné verze např. na wikipedii MAXImalizují celkovou cenu (při zachování celkové velikosti předmětů)
|
Státnice -- Softwarové systémy
Složitost a vyčíslitelnost -- Tvorba algoritmů (10🎓), NP-úplnost (15🎓), Aproximační algoritmy (6🎓), Vyčíslitelné funkce a rekurzivní množiny (8🎓), Nerozhodnutelné problémy (9🎓), Věty o rekurzi (6🎓)
Datové struktury -- Stromy (32🎓), Hašování (13🎓), Třídění (10🎓)
Databázové systémy -- Formální základy: Relace (12🎓), Datalog (9🎓), Ostatní (0🎓) Modely a jazyky: SQL (7🎓), DIS (7🎓), Odborné (3) Implementace: Transakce (5🎓), Indexace (10🎓), Komprese (3)
Softwarové inženýrství -- Programovací jazyky a překladače, Objektově orientované a komponentové systémy, Analýza a návrh softwarových systémů
Systémové architektury -- Operační systémy, Distribuované systémy, Architektura počítačů a sítí
Počítačová grafika -- Geometrické modelování a výpočetní geometrie, Analýza a zpracování obrazu, počítačové vidění a robotika, 2D počítačová grafika, komprese obrazu a videa, Realistická syntéza obrazu, virtuální realita
🎓 - znamená kolikrát byla otázka u státnic