Státnice - Třídění I2
Obsah
Třídění ve vnitřní a vnější paměti (8×🎓)[editovat | editovat zdroj]
Založeno na Třídění (pochází z poznámek k Datovým strukturám, vnější třídění z Organizace a zpracování dat I)
Více prakticky pro I2
09/10: Trídení ve vnitrní a vnejší pameti, casová složitost algoritmu vyjádrená v poctu I/O operací.
14/15: Trídení ve vnitrní a vnejší pameti. Dolní odhady pro usporádání (rozhodovací stromy).
| Zážitky ze zkoušek |
|---|
I1/I4:
|
Třídění založené na porovnávání[editovat | editovat zdroj]
Quicksort[editovat | editovat zdroj]
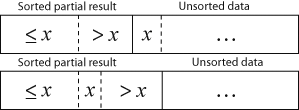
QUICKSORT je asi nejpoužívanější třídící algoritmus, v průměru má při rovnoměrném rozložení nejnižší očekávaný čas. Využívá techniky rozděl a panuj.
Implementace v Haskellu:
qsort [] = [] qsort (pivot:tail) = qsort (filter (< pivot) tail) ++ [pivot] ++ qsort (filter (>= pivot) tail)
Složitost[editovat | editovat zdroj]
nejhorší složitost - pivot špatně: T(n)=T(n-1)+Ө(n)=Ө(n2)
průměr složitost - pivot náhodně: O(n log n)
nejlepší složitost - pivot medián: T(n)=2T(n/2)+O(n) ⇒ a=2 b=2 d=1 ; 2=21 ⇒ Ө(n log n)
O(n) paměti
☀ pro kazdy pevne zadratovany algoritmus volby pivota existuje nejaky vstup, pro ktery alg. bezi v O(n2)
☀ zatimco pri nahodne volbe pivota/hledani medianu je čas horší (multipl.konstanta) než MERGESORT / HEAPSORT pro vsechny vstupy (nahodna volba i hledani medianu chce cas), takže se typicky bere median ze 3-5 pevne danych prvku
☀ pri zohledneni multiplikativni konstanty jde o nejrychlejsi znamy alg. pro trideni zalozeny na vzajemnem porovnavani prvku
Heapsort[editovat | editovat zdroj]
nasypeme prvky do max-haldy a pak je po jednom odebirame O(n log n)
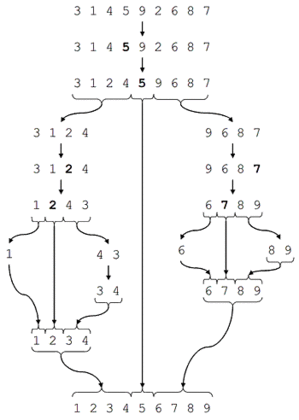
(Adaptabilní) Mergesort[editovat | editovat zdroj]
- projdi posloupnost a rostoucí úseky hazej do fronty - pak je slejvej dokud nemáš jenom 1 úsek
☀ T(n) = 2T(n/2) + Θ(n) ⇒ Θ(n log n)
☀ Je adaptivní na předtříděné posloupnosti a při omezeném počtu rostoucích úseků dosahuje lineární složitosti.
Jednoduchá (sekvenční) třídění[editovat | editovat zdroj]
- SELECTIONSORT třídí vybíráním nejmenšího prvku a jeho prohozením s levým krajním v nesetříděném úseku.
- INSERTSORT vkládá do setříděného úseku další prvek a postupným vyměňováním ho řadí na správné místo.
- BUBBLESORT -- iterativně prochází posloupností a prohazuje inverze
| A-sort - aplikace (a,b)-stromů, vhodný pro částečně setříděné posloupnosti, jinak k ničemu |
|---|
|
Tento algoritmus je aplikací $ (a,b)\,\! $ stromů v třídících algoritmech, vhodnou pro částečně předtříděné posloupnosti. Jinak proti klasickým algoritmům nemá žádné výhody. Pro algoritmus je nutné znát list s nejmenším prvekm FIRST, cestu k němu od kořene a pro každý list ukazatele na následující v uspořádání NEXT. Postup: Odzadu (od "předtříděně největšího") vkládat prvky do stromu modifikovaným A-INSERTem a pak přečíst posloupnost listů (jít po NEXT). A-INSERT pracuje tak, že místo pro vložení prvku hledá od FIRST (jde postupně nahoru po otcích a hledá, kde nejdřív může slézt zas k listům). Složitost: Pomalejší než běžné třídění na libovolná data (asymptoticky stejné), ale rychlejší na částečně předtříděná. Vezmeme $ F\,\! $ -- počet inverzí v posloupnosti. Celk. potřebuju $ O(n)\,\! $ pro načtení prvků, $ O(n)\,\! $ pro všechna štěpení dohromady ze všech běhů A-INSERTu a na každé vložení $ O(h)\,\! $ pro nalezení místa, kde $ h\,\! $ je výška, kam se z FIRST dostanu, přeskočím tak $ f_i\geq a^{h-2}\,\! $ vrcholů (menších než vkládaný) a $ h\in O(\log f_i)\,\! $. Součet $ f_i\,\! $ za $ \forall i\,\! $ dává:
Protože se nepoužívá DELETE, hodí se na toto $ (2,3)\,\! $ stromy. Pro míru $ F\leq n\log n\,\! $ má složitost $ O(n\log\log n)\,\! $, v urč. případech i rychlejší než Quicksort. |
Porovnání algoritmů[editovat | editovat zdroj]
| Algoritmus | Čas nejhůř | Čas $ \varnothing $ | Porov. nejhůř | Porov. $ \varnothing $ | PP | Paměť | AD |
| QUICKSORT | $ \Theta(n^2) $ | $ 9n\log n $ | $ n^2/2 $ | $ 1.44n\log n $ | A | $ n+\log n+c $ | N |
| HEAPSORT | $ 20n\log n $ | $ \leq 20n\log n $ | $ 2n\log n $ | $ 2n\log n $ | A | $ n+c $ | N |
| MERGESORT | $ 12n\log n $ | $ \leq 12n\log n $ | $ n\log n $ | $ n\log n $ | N | $ 2n+c $ | A |
| A-SORT | $ O(n\log(F/n)) $ | $ O(n\log(F/n)) $ | $ O(n\log(F/n)) $ | $ O(n\log(F/n)) $ | A | $ 5n+c $ | A |
| SELECTIONSORT | $ 2n^2 $ | $ 2n^2 $ | $ n^2/2 $ | $ n^2/2 $ | A | $ n+c $ | N |
| INSERTSORT | $ O(n^2) $ | $ O(n^2) $ | $ n^2/2 $ | $ n^2/4 $ | N | $ n+c $ | A |
$ c\,\! $ je nějaká konstanta, $ F\,\! $ značí počet inverzí v posloupnosti, PP -- přímý přístup, AD -- adaptivní na předtříděné.
Pro krátké posloupnosti je do délky $ 22\,\! $ vhodný SELECTIONSORT, do $ 15\,\! $ INSERTSORT, jinak QUICKSORT, což vede k hybridnímu algoritmu. Pro A-SORT jsou nejvhodnější $ (2,3)\,\! $-stromy. Poměr časů QUICKSORT, MERGESORT, HEAPSORT je v průměru $ 1:1.33:2.22\,\! $, platilo to ale v roce 1984 :-).
| Vylepšení Mergesortu |
|---|
| Nedosahuji optimálních výsledků, pokud slévané posloupnosti ve frontách nejsou přibližně stejně dlouhé. Proto provedu úvahu: mějme algoritmus, který slévá rostoucí posloupnosti a uvažujme jeho "slévací" strom $ T\,\! $ (kde posloupnost $ P(v)\,\! $ odp. vrcholu $ v\,\! $ (délky $ l(P(v))\,\! $) vznikne slitím posloupností z jeho synů). Součet časů pro MERGESORT je pak $ O(\sum\{l(P(v))|v\,\! $ vnitřní vrchol $ T\})=O(\sum\{d(t)l(P(t))|t\,\! $ list $ T\}\,\! $. Dále pracujeme jen s délkami posloupností, vytvoříme algoritmus OPTIM, který při slévání sumu minimalizuje -- na začátku dá každé jednoprvkové posl. hodnotu $ c\,\! $, která odpovídá hodnotě jejího prvku (?). Pro slévání vybírá posloupnosti (stromy) s nejmenším $ c\,\! $ a slitému stromu přiřadí $ c_1+c_2\,\! $. Nakonec zbyde v množině stromů jen jeden, a ten je optimální. Pro třídění fronty podle $ c\,\! $ se používá BUCKETSORT. Celkem pracuje v čase $ O(\sum_{i=1}^n l(P_i))\,\! $ na posloupnosti rostoucích úseků $ P_1,\dots,P_n\,\! $. |
Přihrádkové třídění[editovat | editovat zdroj]
lineární třídění, O(n+počet přihrádek) nemusí být rychlejší než klasické algoritmy pokud jim nedáme speciální vstup
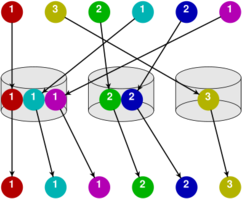
BUCKETSORT[editovat | editovat zdroj]
Třídí jen n přirozených čísel z intervalu <0, m> a to zavedením $ m+1\,\! $ množin, do kterých je rozhází a nakonec tyto spojí do výsledku. Třídění je stabilní pro opakující se prvky, inicializace množin a projití při konkatenaci potřebují $ O(m)\,\! $, rozházení prvků pak $ O(n)\,\! $, takže celkem O(n + m) .
RADIXSORT[editovat | editovat zdroj]
Umí třídit i ve větších intervalech, když používá BUCKETSORT na každou jednotlivou číslici. Protože BUCKETSORT je stabilní, bude to celé fungovat.
- Algoritmus: RADIX-SORT(A, d)
- 1 for i ← 1 to d
- 2 do use a Bucket sort to sort array A on digit i
COUNTINGSORT[editovat | editovat zdroj]
- projdeme pole a poznamenáme si četnosti prvků do pomocného pole, pak projdeme pomocné pole a vždy četnost zvýšíme o četnosti prvnku před ním
- projdeme pomocné pole a podle pole četností (nyní indexy výst.pole) plníme do výstupního pole, vždy po vypsání prvku na výstup snížíme jeho četnost
☀ BUCKETSORT je generalizace COUNTINGSORTU (pokud má BS kyblicky velke 1 degeneruje na CS)
| Příklad COUNTINGSORT |
|---|
|
V příkladu ukážeme, jak setřídit čísel 1, 4, 2, 4, 1, 3, 1. Pomocné pole (číslo - počet výskytů): 1 - 3x 2 - 1x 3 - 1x 4 - 2x Přepočet na hranice prvku (číslo - index konce pole) 1 - 3 2 - 4 3 - 5 4 - 7 V prvním kroce máme umístit číslo 1. Protože víme, že číslo jedna má 3 výskyty, umístíme jej na 3. pozici a snížíme v pomocném poli počet zbývajících výskytů na 2. Pomocné pole po prvním kroku 1 - 2 2 - 4 3 - 5 4 - 7 Další kroky probíhají analogicky, zde je uvedeno, jak se bude postupně plnit seřazené pole: [ ][ ][1][ ][3][ ][ ] [ ][1][1][ ][3][ ][ ] [ ][1][1][ ][3][ ][4] [ ][1][1][2][3][ ][4] [ ][1][1][2][3][4][4] [1][1][1][2][3][4][4] - seřazené pole a algoritmus končí |
Třídění na vnější paměti[editovat | editovat zdroj]
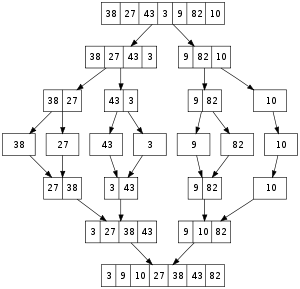
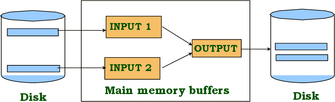
2-cestný MERGESORT na vnější paměti[editovat | editovat zdroj]
- průchod 0: Přečíst stránku setřídit, zapsat (jenom 1 stránka bufferu je použita)
- průchod 1, 2, ..., atd.: (3 stránky bufferu použijeme)
každý průchod čteme a zapisujeme každou stránku do souboru
N stránek v souboru ⇒ počet průchodů 1 + ⌈log₂ N⌉
Celková složitost je: 2N * (1 + ⌈log₂ N⌉)
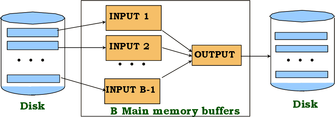
n-cestný MERGESORT na vnější paměti[editovat | editovat zdroj]
Mám soubor s N stránkami a B buffer stránek v RAM:
- průchod 0: použij B stránek, vytvoř ⌈N / B⌉ setříděných běhů pomocí QS nebo HS v paměti, každý má B stránek
- průchod 1, 2, ..., atd.: slij B - 1 běhů
#počet průchodů = 1 + ⌈logB N / B⌉
celková složitost = 2N * #počet průchodů
| Příklad: |
|---|
|
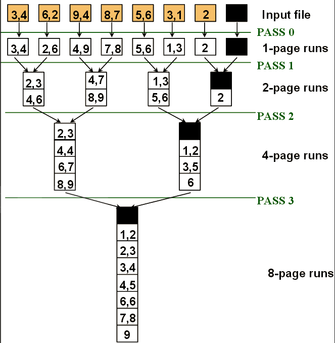
máme 5 stránek v bufferu, budeme třídit soubor s 108 stránkami:
|
| další zdroje |
|---|
|
Dolní odhady pro usporádání (rozhodovací stromy). (🎓🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
Definice (Složitost problému)[editovat | editovat zdroj]
Složitost problému je složitost asymptoticky nejlepšího možného algoritmu, který řeší daný problém (ne nejlepšího známého).
Každý konkrétní algoritmus dává horní odhad složitosti. Dolní odhady (až na triviální -- velikost vstupu, výstupu) jsou složitější.
Věta (Dolní odhad složitosti třídění)[editovat | editovat zdroj]
Pro každý třídící algoritmus, založený na porovnávání prvků, existuje vstupní posloupnost, pro kterou provede $ \Omega(n\log n)\,\! $ porovnání.
Důkaz[editovat | editovat zdroj]
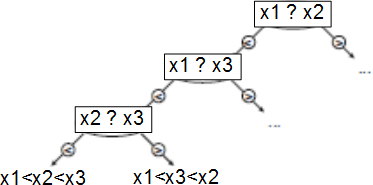
Nakreslím si rozhodovací strom jako model algoritmu A -- všechny vnitřní uzly odpovídají nějakému porovnání, které algoritmus provedl, jejich synové jsou operace, které nasledovaly po různých výsledcích toho porovnání (BÚNO jsou-li prvky různé, bude strom binární). Listy odpovídají setříděným posloupnostem. Pro rovnoměrné rozdělení je očekávaný čas průměrná délka cesty od kořene k listům, nejhorší čas je výška stromu.
Aby byl algoritmus korektní, musí mít strom listy se všemi n! možnými pořadími prvků. Pro plýtvající algoritmus mohou existovat listy, neodpovídající žádné permutaci, tj. porovnává stejnou dvojici prvků dvakrát (a jedna z možností už nemůže nastat). A tedy #listů ≥ n! .
Označím výšku jako h, pak ma nejvýše 2ʰ listů (max.počet listů ⇒ jsou na posl.hladině, na i-té hladině je vrcholů ≤ 2ⁱ )
- a tedy: 2ʰ ≥ #listů ≥ n! a tedy 2ʰ ≥ n!, a to zlogaritmujeme na: h ≥ log n!,
nyní nám stačí odhad faktoriálu: n! ≥ n/2 n/2 ( MiniDk: n! = 1*2*3*... obsahuje alespoň n/2 činitelů větších než n/2 )
- ten zlogaritmujeme: log n! ≥ log(n/2)n/2 = (n/2) log(n/2) ⇒ h ≥ (n/2) log(n/2) ⇒ Ω(n log n )
- ☀ pro šťouraly (n/2) log₂(n/2) $ \stackrel{\text{log podílu je rozdíl log}}{=} $ (n/2) (log₂ n - 1) $ \stackrel{\text{platí pro n ≥ 4}}{≥} $ (n/2) (log₂ n / 2) = (n/4) log₂ n ⇒ h ≥ (n/4) log₂ n ⇒ Ω(n log n )
- ☀ případně můžu použít Stirlingův vzorec n! ≈ $ \sqrt{2\pi n}(\frac{n}{e})^n\,\! $a z pak h ≥ log n! dostáváme Θ(n log n)
- ☀ algoritmy, ktoré "porušují" dolný odhad zložitosti jsou třeba BUCKETSORT
Státnice -- Softwarové systémy
Složitost a vyčíslitelnost -- Tvorba algoritmů (10🎓), NP-úplnost (15🎓), Aproximační algoritmy (6🎓), Vyčíslitelné funkce a rekurzivní množiny (8🎓), Nerozhodnutelné problémy (9🎓), Věty o rekurzi (6🎓)
Datové struktury -- Stromy (32🎓), Hašování (13🎓), Třídění (10🎓)
Databázové systémy -- Formální základy: Relace (12🎓), Datalog (9🎓), Ostatní (0🎓) Modely a jazyky: SQL (7🎓), DIS (7🎓), Odborné (3) Implementace: Transakce (5🎓), Indexace (10🎓), Komprese (3)
Softwarové inženýrství -- Programovací jazyky a překladače, Objektově orientované a komponentové systémy, Analýza a návrh softwarových systémů
Systémové architektury -- Operační systémy, Distribuované systémy, Architektura počítačů a sítí
Počítačová grafika -- Geometrické modelování a výpočetní geometrie, Analýza a zpracování obrazu, počítačové vidění a robotika, 2D počítačová grafika, komprese obrazu a videa, Realistická syntéza obrazu, virtuální realita
🎓 - znamená kolikrát byla otázka u státnic