Formální základy databázové technologie
okruhy 14/15: Relacní kalkuly, relacní algebry, deduktivní databáze. Relacní úplnost. Bezpecné výrazy, ekvivalence relacních dotazovacích jazyku. Veta o tranzitivním uzáveru relace. Sémantika SQL. Datalog, 3 sémantiky a jejich ekvivalence. Datalog s negací, stratifikace. Deduktivní databáze. Rekurze v SQL. Tablo dotazy - statická analýza a optimalizace relacních dotazovacích jazyku. Modelování preferencí, dotazování s preferencemi.
Podle Majklových zápisků: [1] čepičky (🎓) udávají pravděpodobnou důležitost okruhu u státnic.
Obsah
- 1 Relacní kalkuly, relacní algebry. Relacní úplnost. Bezpecné výrazy, ekvivalence relacních dotazovacích jazyku. (12×🎓)
- 2 Věta o tranzitivním uzávěru relace (2×🎓)
- 3 Datalog (7×🎓)
- 4 Sémantika SQL
- 5 Rekurze v SQL. (🎓)
- 6 Tableau dotazy - statická analýza a optimalizace relačních dotazovacích jazyků.
- 7 Tableau dotazy (konjunktivní dotazy)
- 8 Modelování preferencí, dotazování s preferencemi. (nové od 2011)
Relacní kalkuly, relacní algebry. Relacní úplnost. Bezpecné výrazy, ekvivalence relacních dotazovacích jazyku. (12×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
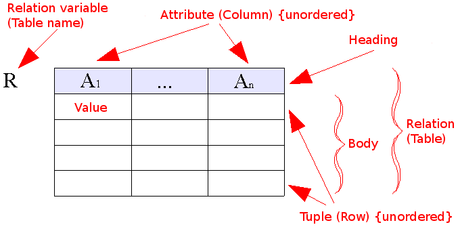
Relační kalkul a relační algebra jsou prostředky relačního modelu dat pro manipulaci s daty
Relační kalkuly (7×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
- neprocedurální jazyky
- relačně úplné, mohou obsahovat nebezpečná pravidla (⇒ silnější než RA)
- vychází z predikátové logiky 1. řádu (při dotazování) relační algebra ne
n-ticový relační kalkul (NRK)[editovat | editovat zdroj]
| př(NRK): spojení (představení * kina):
|
|---|
|
| př(NRK): film, který dávají ve všech kinech, kde něco dávají (P $ = $ PŘEDSTAVENÍ)
|
|---|
|
- pracuje s daty na úrovni n-tic (prvků relace/řádků)
- Termy - n-ticové proměnné, jejich komponenty a konstanty
- Predikáty - jména relací a binární porovnávací predikáty θ (>, <, >=, <=, <>, =)
- Atomické formule R(x), x.A θ y.B, x.C θ 'konstanta', (θ je bin. porov. Predikát), R(t1,....tn) (R predikát, ti je term)
- Atomické formule NRK jsou formule NRK a formule složené z formuli pomocí &, ∨, ¬, ⇒, ⇔ jsou také NRK fle
- Kvantifikátory: ∃, ∀
doménový relační kalkul (DRK)[editovat | editovat zdroj]
| př(DRK): spojení (P$ = $představení * k$ = $kina)
|
|---|
|
- Místo n-tic používá doménové proměnné (tj. atributy = sloupce), místo R.u se používá R(A:x, B:y,...), atribut:typ
- Termy - jednoduché proměnné, konstanty
- Atomické formule R(A1:T1, A2:T2, ...) - stejné jako u NRK
| další zdroje |
|---|
|
|
Relační algebry (3×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
| př.: herci z filmů v kině Mír
|
|---|
|
| př.: kdy je v RA mozne: $ \small(E_1 \times E_2)(selekce) = $ $ \small E_1(selekce) \times E_2 $ ?
|
|---|
|
je neprocedurální jazyk vysoké úrovně pro práci s relacemi v relačním datovém modelu
- 💡 neprocedurální, nicméně struktura výrazu navádí na pořadí a způsob vyhodnocení
- 💡 nemá nebezpečné výrazy
- Relace - má schema (atributy + domény, na pořadí atributů nezáleží ), obsahuje množinu n-tic (duplicity jsou eliminovány)
- Operace - vytvoří z vstupní relace/í výsledek jako novou relaci
- Minimálni množina 6 operací (tvoří rel.algebru AR):
- výběr () (select): - vrací relaci jejíž hodnoty atributů splňují danou podmínku, která může obsahovat jména atributů, konstanty, operátory prorovnávání a logické spojky
- projekce [] (project) - vrací relaci obsahující vybrané sloupce (duplicity jsou eliminovány)
- sjednocení $ \cup $ (union) - vstupní relace musí mít shodnou aritu (stejný počet atributů) a domény atributů musí být stejného typu (duplicity jsou eliminovány)
- množinový rozdíl $ \setminus $ (set difference) - musí platit stejné předpoklady jako u sjednocení
- kartézský součin $ \times $ (Cartesian product) - předpokládá se, že atributy vstupních relací jsou disjunktní (v opačném případě musí být provedeno přejmenování), v praxi mnohdy neproveditelné kvůli vysoké režii
- přejmenování $ ρ $ (rename)
- další odvozené operace
- Průnik $ \cup $ - dá se vyjádřit: $ R_1 \cap R_2 = (R_1 \cup R_2 \setminus (R_1 \setminus R_2))\setminus (R_2 \setminus R_1) $
- Přirozené spojení $ * $ (Natural join) - lze cca vyjádřit pomocí kartézského součinu, selekce a projekce: $ R * S = \left(\left(R \times S\right)\left(Rx = Sx\right)\right)[A \cup B] $
- Spojení přes výraz (normální je přes atributy) = inner join (zobecnění vnitřního spojení)
- Polospojení R <* S. Spojení s projekcí na schema relace, které je menší tj. R
- Levé/Pravé vnější spojení - ve spojení jsou zachovány všechny n-tice z levé/pravé/obou relací, pokud řádky vyhovují podmínkám spojení (v SQL jsou doplněné null, RA toto neumožňuje, jelikož je relačně úplná)
- 💡 Rozdíly mezi Joiny
- Dělení (÷) : Dělíme všechny představení Filmy(režisér=čáp).[jmeno_f]. Vrátí to ntici odpovídajícím všechem kinům, kde všechny filmy režíroval čáp (defakto to vydělí všechny stejný kina čápem a pokud je to jedna tak to vypíše)
- lze vyjádřit pomocí projekce, rozdílu a kartézského součinu: $ R \div S = R[A\setminus B] \setminus ((R[A\setminus B] \times S)\setminus R)[A\setminus B] $
- Dotazovací jazyk Relační algebry - jeden dotaz lze zapsat mnoha způsoby, toho se vyžívá v alg. optimalizaci dotazu
- Jednoduchý dotaz - lze vyjádřit pouze pomocí selekce, projekce a spojení (až 80%) - nejvíc optimalizovány
- Relační úplnost - pokud lze prostředky jazyka lze vyjádřit min.množinou operací $ A_{R} \{(), [ ], \cup, \setminus, \times, rename \} $
- Pozitivní relační algebra $ A_{RP} \{(), [ ], \cup, \times, rename \} $ - je fragment RA vzniklý odstraněním množinového rozdílu
- 💡odpovídá nerekurzivnímu DATALOGu (bez negace)
- Konstantní relace (relace co se nemění po dobu života DB) - např Číselník
| Příklad(srovnání RA, DRK, NRK) |
|---|
|
definujeme rel.schémata: FILM(JMENO_FILMU, JMENO_HERCE) HEREC(JMENO_HERCE, ROK_NAROZENI) Dotaz: Ve kterých filmech hráli všichni herci? RA: $ \small FILM \div HEREC[JMENO\_HERCE] $ NRK:$ ~ \small\{f.JMENO\_FILMU \;|\; \forall herec(HEREC(herec) \Rightarrow f(FILM(f) \wedge\; f.JMENO\_HERCE = herec.JMENO\_HERCE \;\wedge f.JMENO\_FILMU = film.JMENO\_FILMU))\} $ DRK: $ \small\{(f) | FILM(f)\wedge \forall h (HEREC(h) \Rightarrow FILM(f, h))\} $ |
| další zdroje |
|---|
|
|
Bezpečné výrazy (2×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
| bezpečné fle
|
|---|
|
volne proměnné - nejsou v zadnem kvantif. (např R(x)), vázané - jsou v nejakem kvantifikátoru (např: ∃xR(x))
Definujeme: výrazy dotazu $ \{x_1,...,x_k | A(x_1,...,x_k )\} $, $ A $ je formule DRK, databáze $ R* $, dom je doména pro $ R $, aktuální doména formule $ A $ $ adom(A) $ je množina hodnot z relací v $ A $ a konstant v $ A $.
Problém RK jsou nekonečné domény, které je potřeba omezit (aktuální doménou - adom), aby nedocházelo k nežádoucím jevům:
- Nekonečná odpověď v případě nekonečné $ dom $ (např. $ \{ x,y | x=y \} $ )
- situace, kdy TRUE ohodnocení volných proměnných není v DB (např. $ \{ x | ¬Employee(Name: x)\} $ )
- nekonečný výpočet (impl. vyhodnoceni kvantifikace na nekonečné $ dom $) (např. $ \{ x | ∀y R(x,...,y) \} $ kde y má nekon.doménu )
řešením jsou doménově nezávislé (definitní, určité) dotazy $ DRK^{ind} $
- tj.: nejsou definitní pokud pod ruznymi $ dom $ davaji ruzne vysledky
- bezpečná formule ⇒ je také doménově nezávislá (opačně to neplatí, dom.nezávislé jsou nadmnožinou bezpečných)
| další info |
|---|
|
další sémantiky (stejně silné), které uvedené problémy řeší:
$ DRK^{out}≅DRK^{lim}≅DRK^{ind} $ |
zjistit, zda je DRK výraz dom.nezávislý je nerozhodnutelný problém (∄program co zjisti jestli je dom.nezávislý) a tedy $ DRK^{ind} $ není rek.spočetný jazyk
máme ale jednoduchá syntaktická pravidla (třídu) která nám určují bezpečné formule (jsou podmnožinou dom.nezávislých):
Bezpečné formule DRK[editovat | editovat zdroj]
| př: bezpečná pravidla DRK: |
|---|
|
| př: nebezpečná pravidla NRK
|
|---|
|
- nemají ∀
- ( $ ∀x~ φ(x) $ můžeme nahradit $ ¬∃x (¬φ(x)) $ )
- každá disjunkce $ \varphi_1 \or \varphi_2 \or ... $obsahuje stejné volné proměnné
- ( $ \varphi_1 \Rightarrow \varphi_2 $ tranformujeme na $ ¬\varphi_1\or\varphi_2 $ )
- každá konjunkce (maximální), $ φ \equiv φ_1∧...∧φ_r $má všechny volné proměnné omezené, tj. platí pro ni alespoň 1 z podmínek:
- (a) proměnná je volná v $ \varphi_i $co není negace ani binární porovnání
- (b) ∃$ \varphi_i\equiv x=a $, kde $ a $ je konstanta nebo omezená proměnná
- ¬ smí být pouze v konjunkcích z bodu 3
| další zdroje |
|---|
|
Bezpečné (safe) formule NRK[editovat | editovat zdroj]
| syntaktická pravidla pro bezpečné výrazy v NRK (nebylo na přednášce) |
|---|
|
| př: nebezpečná pravidla Datalog
|
|---|
|
z přednášky:
z media:Datalog-unsafe_rules.PNG:
(ve všech připadech nekonečnost X splni pravidlo i když je R konečná relace) |
Bezpečné pravidla v Datalogu[editovat | editovat zdroj]
- Omezená proměnná x v Datalogu je taková, která se vyskytuje v těle literálu L a pro jehož tělo platí:
- L je dán pravým predikátem, nebo
- pravý predikát - jméno zákl.db relace nebo jméno virtuální relace (prakticky EDB nebo levá strana IDB pravidla)
- L je x = a nebo a = x , kde a je konstanta nebo omezená proměnná
- L je dán pravým predikátem, nebo
Pravidlo je bezpečné pokud jsou ∀proměnné omezené.
Datalog má povolená pouze bezpečná pravidla a dále platí, že v hlavách jsou pouze jména virtuálních relací
- 💡 (ktere nejsou v EDB), tzn odvozováním nevytvářím další základní data
Ekvivalence dotazovacích jazyků[editovat | editovat zdroj]
- NRK omezený na bezpečné výrazy je ekvivalentní $ A_{R} $ (relační algebře)
- Z toho plyne, že kalkulové jazyky lze realizovat pomocí $ A_{R} $, která je relativně dost silná (ale nemá na logiku 1. řádu - Datalog)
- DRK omezený na bezpečné výrazy je ekvivalentní $ A_{R} $
💡 DRK s doménově nezávislými výrazy je silnější než $ A_{R} $
- NRK omezený na bezpečné výrazy je ekvivalentní DRK omezenému na bezpečné výrazy
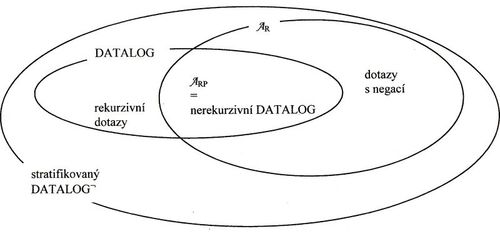
- Datalog je silnější než $ A_{RP} $ (pozitivní RA)
- Tranzitivní uzávěr (rekurze)
- V datalogu nelze vyjádřit rozdíl, proto není silnější než obyč RA
- Stratifikovaný Datalog¬ je silnější než $ A_{R} $
- tranzitivní uzávěr (rekurze)
- rozdíl lze vyjádřit pomocí negace
💡 Stratifikovaný nerekurzivní Datalog¬ je ekvivaletní $ A_{R} $
Relační úplnost (2×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
relačně úplný jazyk - má prostředky přímo realizovat všechny operace $ A_R $ ( tj. "minimalne tak silny jako RA" )
Relačně úplný je:
- NRK, DRK (s bezpecnymi vyrazy jsou ekvivalentní $ A_{R} $)
- SQL (silnější, protože má navíc agregační fce, aritmetiku, null...)
💡 Datalog¬ (Stratifikovaný nerekurzivní Datalog¬ je ekvivaletní $ A_{R} $)
| další zdroje |
|---|
|
Věta o tranzitivním uzávěru relace (2×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
Binární relace R je tranzitivní, jestliže ∀abc: (a,b)∈R ∧ (b,c)∈R ⇒ (a,c)∈R.
Tranzitivní uzávěr Rₛ⁺ relace R, je nejmenší tranzitivní relace obsahující R.
- v praxi užitečný – např. hledání spojení s přestupy v dopravě, nebo hledání nejkratší cesty v grafu, apod.
Věta (TC nemůže být vyjádřen v RA ): Pro schéma binární relace R v AR neexistuje výraz, který ∀ relaci R počítá její tranzitivní uzávěr R⁺.
Pozn: 💡 Nestačí ani rozšíření o aritmetické výrazy, agregační fce a ano/ne dotazy, částečné řešení poskytuje Datalog
| Lemma E(Rₛ): |
|---|
|
lze se na to dívat tak, že:
|
Dk (sporem, nechť takové E existuje (je konečné), pak dokážu zvýšit d natolik, že aₘaₘ₊d ∉ E(Rₛ) nebo aₘ₊daₘ ∈ E(Rₛ) a nemělo by být)[editovat | editovat zdroj]
- uvažujme binární relaci Rₛ = { aᵢaⱼ | 1 ≤ i < s } ⇒ jejím tranzitivním uzávěrem je Rₛ⁺ = {aᵢaⱼ: i < j}
- ukážeme, že ∄ výraz E(Rₛ) = Rₛ⁺, ∀s
- Lemma: každý RA výraz E můžeme pro dost.velké s vyjádřit jako: E(Rₛ) ≅ { b₁,...,bₖ | Γ(b₁,...,bₖ) }, kde Γ je v DNF
- bᵢ = aⱼ , bᵢ ≠ aⱼ ,
- bᵢ = bⱼ + c nebo bᵢ ≠ bⱼ + c, kde c je (ne nutně kladná) konstanta,
- Dk: indukcí dle počtu operátorů v E
- sporem, nechť takové E existuje, pak můžeme d zvýšit natolik že:
- díky konečnému počtu atomických formulí v Γ: aₘaₘ₊d ∉ E(Rₛ) nebo
- pomocí ≠: aₘ₊daₘ ∈ E(Rₛ) (💡 obojí je spor se definicí TC)
- Tedy: Pro jakýkoliv výraz E vždy existuje s pro něž E(Rₛ) ≠ Rₛ⁺
| Dk (detailně z přednášky s poznámkami - NEvyžaduje se ke zkoušce) |
|---|
|
| další zdroje |
|---|
V češtině u Prof. Pokorného na slajdech. A pokud to někdo náhodou stále nechápe, tak jako já, tak doporučuji materiály z jedné nizozemské univerzity, kde je dopodrobna rozebrán jak důkaz lemmatu, tak hlavního teorému: Lemma1 MainTheorem
|
Datalog (7×🎓)[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
Deduktivní databáze[editovat | editovat zdroj]
| př. EDB: |
|---|
|
| př. IDB: |
|---|
|
| př. dotazy: |
|---|
|
je db systém, který dokáže provádět dedukce (např. odvodit další fakta) založené na faktech a pravidlech uložených v (deduktivní) db
Deduktivní db se skládá z:
- Extenzionální db (EDB) (uložené tabulky) - tvořené fakty
- fakta - tvrzení, atomické fle obsahující pouze konstanty (statická data, základní informace) - tj. základní literály
- termy - proměnné nebo konstanty
- fakta - tvrzení, atomické fle obsahující pouze konstanty (statická data, základní informace) - tj. základní literály
- Intenzionální db (IDB) (virtuální relace ≈ "pohledy" z SQL) - množina pravidel:
hlava :- tělo- pravidla (v IDB) - jsou Hornovy klausule
L₀ :- L₁,…,Lₙ(návod jak odvodit data, která nejsou explicitně uložena)- literály
Lᵢ- jsou atomické formule (nebo negace a.f.) ve tvaruP(t₁,..,tₖ), kdePje predikátový symbol atᵢje proměnná nebo konstanta -
L₀hlava pravidla,L₁,…,Lₙtělo pravidla - 💡 tvrzení i literály jsou Hornovy klauzule
- literály
- dotazy - výraz jehož výsledkem jsou nalezená a odvozená data
- pravidla (v IDB) - jsou Hornovy klausule
- Integritní omezení (IO)
- tvrzení vymezující korektní DB (na konceptuální a db úrovni)
- př: název_k jednoznačně identifikuje řádky tabulky Kina
- jsou výsledkem snahy kombinovat logické programování s relačními db za účelem vytvořit systém, který podporuje mocný formalismus (s vyjadřovacími schopnostmi logických prog. jazyků) a je stále rychlý a schopný pracovat s velmi rozsáhlými objemy dat.
- mají větší vyjadřovací schopnosti než relační db, ale menší než logické programovací jazyky
| další zdroje |
|---|
|
|
Datalog, 3 sémantiky a jejich ekvivalence.[editovat | editovat zdroj]
jazyk používaný v deduktivních db je Datalog - (data)logický program je množinou tvrzení a pravidel
- 💡 vychází z PROLOGu (Datalog je podmnožinou PROLOGu) a využívá vyhodnocovací algoritmy umožňující efektivnější implementaci (operace relační algebry)
| př: nebezpečná pravidla Datalog
|
|---|
|
z přednášky:
z media:Datalog-unsafe_rules.PNG:
(ve všech připadech nekonečnost X splni pravidlo i když je R konečná relace) |
Bezpečné pravidla v Datalogu[editovat | editovat zdroj]
- Omezená proměnná x v Datalogu je taková, která se vyskytuje v těle literálu L a pro jehož tělo platí:
- L je dán pravým predikátem, nebo
- pravý predikát - jméno zákl.db relace nebo jméno virtuální relace (prakticky EDB nebo levá strana IDB pravidla)
- L je x = a nebo a = x , kde a je konstanta nebo omezená proměnná
- L je dán pravým predikátem, nebo
Pravidlo je bezpečné pokud jsou ∀proměnné omezené.
Datalog má povolená pouze bezpečná pravidla a dále platí, že v hlavách jsou pouze jména virtuálních relací
- 💡 (ktere nejsou v EDB), tzn odvozováním nevytvářím další základní data
Sémantiku logických programů je možné vybudovat minimálně třemi různými způsoby:
logicko-odvozovací přístup (Proof-Theoretic Approach)[editovat | editovat zdroj]
- Metoda: interpretace pravidel jako axiomů použitelných k důkazu, tj. provádíme substituce v těle pravidel a odvozujeme nová tvrzení z hlavy pravidel. V případě DATALOGu tak lze získat právě všechna odvoditelná tvrzení.
logicko-modelový přístup (Model-Theoretic Semantics)[editovat | editovat zdroj]
- Predstavme si to jako model v logice (analogicke pro logicko-odvozovaci pristup, kde je to take stejne jako v logice - take se z "axiomu" odvozuji vsechna tvrzeni).
- Metoda: za predikátové symboly dosadíme relace tak, aby na nich byla splněna pravidla.
Příklady z přednášky:
|
Uvažujme logický program LP IDB: P(x) :- Q(x)
Q(x) :- R(x)
tj. Q a P označují virtuální relace.
R(1) Q(1) P(1) Q(2) P(2) M₁ P(3)
|
R(1) Q(1) P(1) M₂
|
💡 při obou sémantikách obdržíme stejný výsledek.
Nevýhody obou přístupů: neefektivní algoritmy v případě, že EDB je dána databázovými relacemi.
| příklad MPB: |
|---|
%EDB: muž(Honza) %IDB: nudný(x) :- ¬zábavný(x), muž(x) zábavný(x) :- ¬nudný(x), muž(x) pak instance databáze
I1: {nudný = {Honza}, zábavný = Ø}
I2: {nudný = Ø, zábavný = {Honza}}
jsou dva MPB (💡 IDB obsahuje neg.cyklus) |
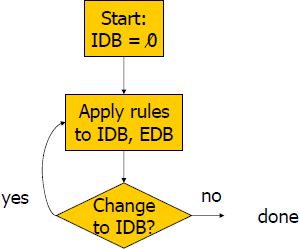
pomocí pevného bodu zobrazení (Fixpoint Semantics)[editovat | editovat zdroj]
- Metoda: vyhodnocovací algoritmus + relační db stroj
Nejmenší pevný bod (NPB) rovnice $ R = f(R) $(kde R je bin.schéma relace) je relace $ R^* $ taková, že platí:
- $ R^* = f(R^*) $ (pevný bod)
- $ S^* = f(S^*) ⇒R^*⊆ S^* $ (minimalita)
Minimální pevný bod (MPB) pro program je takový pevný bod R*, že neexistuje žádný další pevný bod, který je vlastní podmnožinou R*.
Z toho plyne:
- ∃ nejmensi pevny bod (NPB), pak je jediným MPB.
- Existuje-li více MPB, pak jsou navzájem neporovnatelné a NPB neexistuje.
| další zdroje |
|---|
|
Datalog s negací, stratifikace.[editovat | editovat zdroj]
| Zážitky ze zkoušek |
|---|
|
$ A_{RP} \{(), [ ], \cup, \times, rename \} $ (pozitivní RA)
Datalog¬[editovat | editovat zdroj]
- Datalog je silnější než $ A_{RP} $, ale existují dotazy v $ A_R $, které v Datalogu nelze vytvořit,
- např.:"kteří překladatelé nepřekládají do angličtiny": PŘEKLÁDÁ[JMÉNO] – (KVALIFIKACE(JAZYK=‘ANGL’)[JMÉNO])
- k vyjádření takovýchto dotazů (obsahujících v relační algebře rozdíl) potřebuje Datalog negaci – je označován Datalog s negací, ovšem způsoby vyhodnocení programů v tomto jazyce obecně nevedou k jednoznačně definovaným virtuálním relacím – proto je identifikována podmnožina Datalogu s negací, která tuto jednoznačnost zajišťuje – tzv. stratifikovaný Datalog (viz dále)
stratifikace[editovat | editovat zdroj]
- jedná se o rozvrstvení pravidel do vrstev tak, aby byla zajištěna jednoznačnost vyhodnocování programů
- definujeme pojem definice virtuální relace S, což je množina všech pravidel, kde se S vyskytuje v hlavě
- Program $ P $ je stratifikovatelný, jestliže existuje disjunktní dělení $ P = P_1 ∪ P_2 .... ∪ P_n $ takové, že plati:
- vyskytuje-li se predikátový symbol $ S $ pozitivně (je-li obsažen v pozitivním literálu v těle pravidla) v nějakém pravidle $ P_i $, pak je jeho definice obsažena v $ \bigcup_{1 ≤ k ≤ i}P_k $
- 💡 tj. jeho definice může být ve stejné nebo nižší vrstvě
- vyskytuje-li se predikátový symbol $ S $ negativně (je-li obsažen v negativním literálu v těle pravidla) v nějakém pravidle $ P_i $, pak je jeho definice obsažena v $ \bigcup_{1 ≤ k < i}P_k $
- 💡 tj. jeho definice musí být pouze v nižší vrstvě
- vyskytuje-li se predikátový symbol $ S $ pozitivně (je-li obsažen v pozitivním literálu v těle pravidla) v nějakém pravidle $ P_i $, pak je jeho definice obsažena v $ \bigcup_{1 ≤ k ≤ i}P_k $
- Dělění $ P_1,…, P_n $ se nazývá stratifikace $ P $, každé $ P_i $ je stratum (stratifikace se píše s čárkami pže záleží na pořadí).
- zjišťování, zda je program stratifikovatelný (a nalezení konkrétního dělení) se provádí pomocí závislostních grafů s ohodnocenými hranami (poz/neg podle výskytu pravidla), jestliže se v grafu vyskytuje cyklus s negativní hranou, není program stratifikovatelný
- když je program stratifikovatelný ⇒ má MPB
Příklady z přednášky:
P(x) :- ¬ Q(x) (1) R(1) (2) Q(x) :- Q(x), ¬ R(x) (3)
P(x) :- ¬ Q(x) Q(x) :- ¬ P(x)
A(x,x):-METRO(u,x,y) (1) A(x,y):-A(x,z),METRO(u,z,y) (2) B(x,z):-A(x,y),A(z,y),x!=z (3) O1(y):-A(y,Skalka),y!=Krizikova (4) O2(z):-B(z,Krizikova) (5)
|
%EDB dil(trojkolka, kolo, 3). dil(trojkolka, rám, 1). dil(rám, sedadlo, 1). dil(rám, pedál, 2). dil(kolo, ráfek, 1). dil(kolo, pneumatika, 1). dil(pneumatika, ventilek, 1). dil(pneumatika, duse, 1). %IDB velky(P) :- dil(P,S,Q), Q > 2. maly(P) :- dil(P,S,Q), not velky(P).
|
Tvrzení: Nerekurzivní programy DATALOG¬u vyjadřují právě ty dotazy, které jsou vyjádřitelné v $ A_R $.
předpoklad uzavřeného světa[editovat | editovat zdroj]
| (možná už není ve státnicích) |
|---|
* předpoklad uzavřeného světa (CWA) je metapravidlo k odvozování negativní informace
|
| další zdroje |
|---|
| př. rektifikace: |
|---|
|
P(a,x,y) :- R(x,y) P(x,y,x) :- R(y,x) zavedeme u,v,w , substituce: P(u,v,w) :- R(x,y), u = a, v = x, w = y P(u,v,w) :- R(y,x), u = x, v = y, w = x ⇒ P(u,v,w) :- R(v,w), u = a,
|
Algoritmy vyhodnocení dotazů v Datalogu a Datalogu s negací[editovat | editovat zdroj]
Obecne pred vyhodnocenim programu se provadi rektifikace - hlavy se stejnym predikatem maji po řadě stejne pojmenovane promenne.
- 💡 Lemma: rektifikace zachovává bezpečnost a je ekvivaletní původnímu výrazu
Nerekurzivní program[editovat | editovat zdroj]
| př. algoritmu pro nerekurzivní program: |
|---|
|
C(x,y) :- F(x1,x), F(x2,y), S’(x1,x2)
|
Jedna se o nerekurzivní program, tedy graf je acyklický. Z toho plyne existence topologického uspořádání. Podle tohoto uspořádání zpracovávám virtuální relace.
- pravou stranu převeď na spojení a selekci
- proveď na výsledek projekci
- předchozí dvě pravidla proveď pro všechna pravidla se stejnou hlavou a výsledek sjednoť
💡 tj. v grafu začnu od uzlu ve kterém končí cesty a znej postupuji zpet k dalsim uzlum a je podle nej vyhodnocuji
Rekurzivní program[editovat | editovat zdroj]
|
|
Datalog¬[editovat | editovat zdroj]
Mejme priklad:
zajimavy(X) :- ¬nudny(X), muz(X). nudny(X) :- ¬zajimavy(X), muz(X).
Extenzionalni tabulka muz obsahuje jeden zaznam 'Honza'. Pak dostavame dva minimalni pevne body (v Datalogu neni zaruceno poradi vykonavani pravidel):
- {zajimavy={Honza}, nudny=Ø}
- {nudny={Honza}, zajimavy=Ø}
Tento problem neexistence nejmensiho pevneho bodu (i neexistence nejmensiho modelu pro logicko-modelovy přístup + neexistence odvozeni pro logicko-odvozovaci přístup) resi stratifikace (viz definice).
Stratifikovaný DATALOG¬[editovat | editovat zdroj]
- Předpoklady: pravidla jsou bezpečná, rektifikovaná.
- použije se alg. vyhodnocení Datalogu bez negace, akorát místo případné ¬Q se použije: $ adom^n – Q $
- 💡 $ adom $ - aktuální doména programu, tj. sjednocení všech konstant z EDB a IDB, $ n $ je počet atributů v Q
| další zdroje |
|---|

Sémantika SQL[editovat | editovat zdroj]
Rekurze v SQL. (🎓)[editovat | editovat zdroj]
Tableau dotazy - statická analýza a optimalizace relačních dotazovacích jazyků.[editovat | editovat zdroj]
Statická analýza (relačních dotazovacích jazyků) chápeme ve smyslu statické analýzy programovacích jazyků (viz Static code analysis) - analýza (kódu) dotazů bez vykonávání programů z nich vytvořených (bez dynamické analýzy). Lze ji vykonat automatizovaným nástrojem ale také formálními metodami které dokazují vlastnosti dotazů.
- Obvyklé cíle statické analýzy programovacích jazyků (a tedy i relačních dotazovacích jazyků):
- odhalení chyb
- Optimalizace jako součást kompilace
- Odhad složitosti úloh
- Bezpečnost, …
Tableau dotazy (konjunktivní dotazy)[editovat | editovat zdroj]
umí jen selekci, projekci a kartezsky součin (tedy i join) - používají se k ilustraci principů statické analýzy (na matfyzu :P)
tableau query = tabulkové dotazy ≈ konjunktivní dotazy DRK ≈ QBE - query by example
Věta: Pro každý omezený relační výraz E (selekce, projekce, přirozené spojení s disjunktními proměnnými) existuje T-dotaz q = (T; u) tak, že pro každou instanci I platí E(I) = q(I).
- Příklad
- Relace: R(A,B,C), S(C,D,E) RA dotaz: (R*S)(C=4)[A,B]
- Tablo dotaz:
- q = (T,u)
- T = R(xA,xB,4), S(4,xD,xE)
- u = <A:xA, B:xB>
- zápist T tabulkou:
| R | A | B | C |
| xA | xB | 4 |
| S | C | D | E |
| 4 | xD | xE |
Glogální optimalizace - Homomorfismus tableau dotazů[editovat | editovat zdroj]
Lokální optimalizace - klasická optimalizace třeba SQL přeuspořádáním stromu dotazu.
Globální optimalizace - vymaže vícero zbytečných spojení.
q₁ = (T₁, u₁) a q₂ = (T₂, u₂) jsou tablo dotazy, homomorfismus q₂ → q₁ je substituce θ taková, že θ(T₂) ⊆ T₁ a θ(u₂) ⊆ u₁.
Věta: q₁ ⊆ q₂ ⇔ existuje homomorfismus q₂ → q₁.
Řekneme, že tablo dotaz (T, u) je minimální, když neexistuje dotaz (S, v) ekvivalentní s (T, u) a |S|<|T| (tedy ostře méně spojení).
Příklad:
Substituce (homomorfismus) z (b) na (a):
- x₁ v (b) je to samé jako x v (a). Stejne tak y₁ v (b) je to samé jako y v (a).
- x,y zůstává.
- Je vidět, že (a) má v sobě všechny podmínky co upravene (b), takže výsledny homomorfismus je podmnožinou (a).
- Tudiz (a) je podmnozinou (b)
Substituce z (c) na (b):
- x₂ v (c) je to samé jako x₁ v (b). Stejne tak y₂ v (c) je to samé jako y₁ v (b).
- x,x₁,y,y₁ zůstává.
- Je vidět, že (b) má v sobě všechny podmínky co upravene (c), takže výsledny homomorfismus je podmnožinou (b).
- Tudiz (a) je podmnozinou (c)
Substituce z (d) na (c):
- x₁ v (d) je to samé jako x₂ v (c).
- x,y,y₁ zůstává.
- Je vidět, že (c) má v sobě všechny podmínky co má (d), takže výsledek bude podmnožinou výsledku (d)
Statická analýza - Složitosti[editovat | editovat zdroj]
- co-r.e. ... co-rekursivne spocetne
- ¬r. ... neni rekurzivni
| inkluze | splnitelnost | |
|---|---|---|
| T-dotazy | NP úplné | ano |
| DRK | co-r.e. a ¬r. | r.e. a ¬r. |
| Datalog | ¬r. | r. |
Veta: Necht q a q' jsou T-dotazy. Pak nasledujici jsou NP-uplne problemy:
- (a) q ⊆ q' (problém existence homomorfismu)
- (b) q ≡ q'
Veta (Datalog): Splnitelnost IDB relace r programem P je rozhodnutelna.
Modelování preferencí, dotazování s preferencemi. (nové od 2011)[editovat | editovat zdroj]
Hledání optimalizované na preference uživatele ( pomáháme uživateli najít to co opravdu chce, nebo co si myslíme že by se mu mohlo líbit )
- Vyjádření preference - preferenční relace (porovnání x je lepší než y) vs. hodnotící funkce (x je dobrý na 5 hvězdiček, palec nahoru...).
- Explicitní vyjádření (vědomá akce) vs Implicitní vyjádření (chování se např. v eshopu - otevření detailů, prohlížení fotek, ...)
Modely preferencí a jejich učení[editovat | editovat zdroj]
Model založený na atributech, kolaborativní filtrování, preferenční relace, hybridní modely
- Model preferencí umožňuje zjistit, jak je některý objekt preferovaný. Vytváří se z chování uživatele
- Model založený na atributech
- Využívá atributů hodnocených položek
- Učení se sestává ze dvou kroků - lokální preference (normalizace hodnot atributů), globální preference (agregace ohodnocení a projekce vektorů do [0, 1])
- Kolaborativní filtrování
- Najdu si množinu V uživatelů podobných uživateli U, kterým se líbí stejné věci
- „Zákazníci, kteří si koupili x si také koupili y“
- K výpočtu vzdáleností se používáji váhy sousedů, počítá se kosinova míra, pearsonova korelace ....
- Implementace - inmemory, bayesovy sítě, predikční modely...
- Preferenční relace
- Užívané v ekonomii
- Porovnání objektů – x je lepší než y
- Neumožňuje jednoduché setřídění objektů podle aktuální vhodnosti
- Vytvořeno podle lidského uvažování - Přirozené pro uživatele, ale možná moc složité
- P(x,y) - mám radši y než x, R(x,y) - y je alespoň tak dobrá jako x, I(x,y) - mezi x a y nedokážu rozlišit, jsou stejně dobré
- CP-sítě Conditional probability networks
| další zdroje |
|---|
Státnice -- Softwarové systémy
Složitost a vyčíslitelnost -- Tvorba algoritmů (10🎓), NP-úplnost (15🎓), Aproximační algoritmy (6🎓), Vyčíslitelné funkce a rekurzivní množiny (8🎓), Nerozhodnutelné problémy (9🎓), Věty o rekurzi (6🎓)
Datové struktury -- Stromy (32🎓), Hašování (13🎓), Třídění (10🎓)
Databázové systémy -- Formální základy: Relace (12🎓), Datalog (9🎓), Ostatní (0🎓) Modely a jazyky: SQL (7🎓), DIS (7🎓), Odborné (3) Implementace: Transakce (5🎓), Indexace (10🎓), Komprese (3)
Softwarové inženýrství -- Programovací jazyky a překladače, Objektově orientované a komponentové systémy, Analýza a návrh softwarových systémů
Systémové architektury -- Operační systémy, Distribuované systémy, Architektura počítačů a sítí
Počítačová grafika -- Geometrické modelování a výpočetní geometrie, Analýza a zpracování obrazu, počítačové vidění a robotika, 2D počítačová grafika, komprese obrazu a videa, Realistická syntéza obrazu, virtuální realita
🎓 - znamená kolikrát byla otázka u státnic